NOTIONS ELEMENTAIRES DE LA THEORIE DES ENSEMBLES ET DE TOPOLOGIE
3ème partie
1-Relation d’équivalence sur un ensemble
On donne un ensemble E non vide quelconque. Soit Ω une relation dans E.
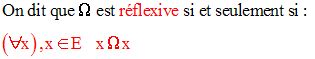
Exemple :
L’égalité, notée =, dans N est réflexive car tout entier n est égal à lui-même.
On écrit n = n.
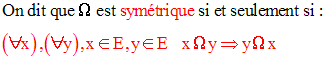
Exemple :
L’égalité dans N est symétrique puisque pour tous entiers p et n, on a :
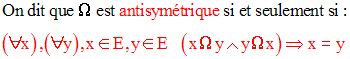
Exemples :
Il est évident que l’égalité dans N est antisymétrique.
Soit maintenant la relation « … divise… » définie dans N*.
On notera « | » cette relation.
Ainsi « 2 divise 4 » sera noté : 2 | 4.
Montrons que cette relation est antisymétrique.
Soient deux entiers non nuls quelconques a, b.
Si a | b alors il existe un entier q non nul tel que b = aq.
Si b | a alors il existe un entier q’ non nul tel que a = bq’.
Donc b = aq = (bq’)q = b(qq’) et ceci implique que 1 = qq’ puisqu’on peut simplifier par b non nul.
Dans N* , l’équation qq’ = 1 n’est vraie que pour q = q’ = 1 et ainsi a = b.
Conclusion :
a | b et b | a implique a = b ; donc la relation | définie dans N* est antisymétrique.

Exemple
L’égalité dans N est transitive.
Exercice
Montre que la relation de divisibilité dans N* , notée « | », est transitive.
On dit que Ω est une relation
d’équivalence sur un ensemble E si et seulement si elle est
simultanément
réflexive, symétrique,
transitive.
Exemple
L’égalité dans N est à la fois réflexive,
symétrique, transitive.
Donc elle est, dans N, une relation
d’équivalence.
Exercice
La relation de divisibilité dans N* , notée « | », est-elle une relation d’équivalence ?
Soit Ω une relation d’équivalence sur un ensemble E.
Pour tout élément a de E, on appelle classe d’équivalence de a la partie de E :
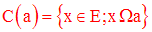
On peut facilement montrer l’équivalence logique suivante :
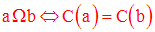
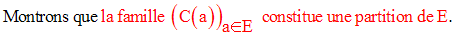

Exercice
Montre que la réciproque est vraie, c’est-à-dire :
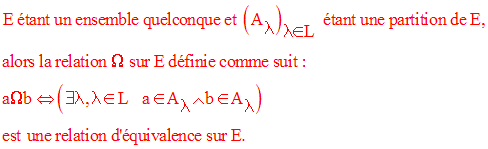
L’ensemble des classes d’équivalence est appelé ensemble quotient de E par Ω.
Cet ensemble sera noté : E / Ω
Exercice
On donne un ensemble E = {a, b, c}. f est une relation sur E définie par son graphe :
Gf = {(a,a) ; (b,b) ; (c, c) ; (a,b) ; (b,a) ; (a,c) ; (c,a) ; (b,c) ; (c,b)}
Dessine le schéma cartésien de f.
La diagonale principale de ce schéma est-elle entièrement remplie ? Que peut-on en déduire ?
Comment les points (x,f(x)) se positionnent-ils par rapport à cette diagonale ? Que peut-on en déduire ?
Montre que f est transitive et déduis que f est une relation d’équivalence sur E.
Définis par extension E / f.
2-Relation d’ordre sur un ensemble
On appelle relation d’ordre
sur un ensemble E une relation dans E qui est simultanément
réflexive, antisymétrique, transitive.
On dira que E est ordonné par cette relation.

Exemples
L’égalité sur un ensemble quelconque non vide est une relation d’ordre appelée ordre trivial.
E étant un ensemble quelconque non vide. L’inclusion dans P(E) est une relation d’ordre sur P(E).
Soit un ensemble E ordonné par la relation d’ordre R.
Deux éléments a, b de E tels que aRb ou bRa sont dits comparables.
Exemple et contre-exemples
N est ordonné par la relation d’inégalité ≤.
De plus, on a la tautologie :

On dira donc que deux éléments quelconques de N sont comparables.
P(E) est ordonné par l’inclusion. Cependant, il existe au moins deux éléments A, B tels que :

Il suffit par exemple de prendre deux sous ensembles de E dont l’intersection est vide.
Dans ce cas, on dira que A, B ne sont pas comparables.
N est ordonné par la relation « … divise … »,
notée « | ».
Cependant il existe au moins deux entiers naturels a et b tels que ni a | b,
ni b | a.
On dira que a, b ne sont pas comparables.
Il suffit de prendre a = 2 et b = 3.
Une relation d’ordre R dans un ensemble E est dite d’ordre
total si deux éléments quelconques
de E sont
comparables.
Dans le cas contraire, c’est-à-dire s’il existe au
moins deux éléments de E non comparables
on dira que l’ordre est partiel.
3-Relation d’ordre strict sur un ensemble
Soit E un ensemble quelconque non vide. Un relation R dans
E est dite relation d’ordre strict
si et
seulement si :
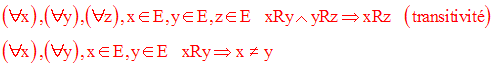
On dit que E est strictement ordonné par R.
Exercice
Montre que l’inégalité stricte < dans N est une relation d’ordre strict total.
On donne un ensemble E non vide quelconque.
Montre que l’inclusion stricte R définie dans P(E) par :
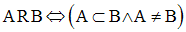
est une relation d’ordre strict partiel.
Exercices de récapitulation
1)
Montre que si R est une relation d’ordre
strict sur un ensemble E, alors xRy et
yRx ne sont
jamais simultanément vraies.
2)
a-
On donne A un ensemble non trivialement ordonné par une relation, notée ≤.
Montre que la relation R sur A définie par :
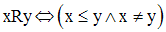
est un ordre strict sur A.
b-
La somme suivante :
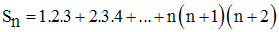
est-elle égale à :
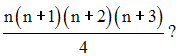
(Raisonne par récurrence sur n)
3)
a-
Soit B un ensemble strictement ordonné par une relation, notée <.
Montre que la relation S sur B définie par :
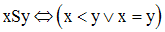
est une relation d’ordre sur B.
b-
Montre par récurrence sur n (n entier naturel) que :
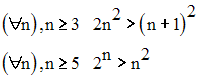
Solution
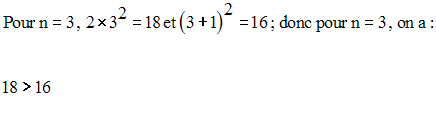
La propriété est vérifiée pour n = 3.

On a :
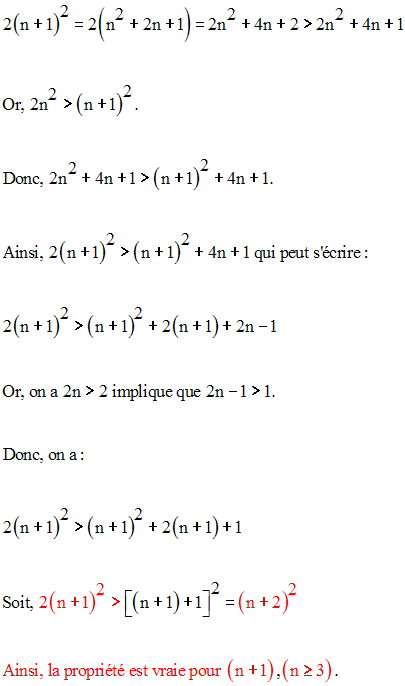
On a :

4)
Soit N l’ensemble des entiers naturels.
Soit n un élément quelconque de N, différent de 0.
Deux entiers naturels quelconques a, b sont dits congrus modulo n, et on écrit :

si et seulement si la division de a, b par n donne le même reste.
Supposons a > b.
La division de a et b par n donne le même reste r est
logiquement équivalent à dire qu’il existe k1 et k2
deux entiers naturels tels que :
a = k1 n + r et b = k2 n + r ou a – b = (k1 – k2 )n
Posons k1 – k2 = k. Puisque a > b, k1 – k2 = k > 0.
On obtient ainsi l’équivalence logique :
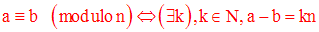
Exemples
La division de 17 et de 29 par 3 donne 2 pour reste ; alors on a :
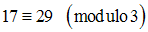
16 et 5 ne sont pas congrus modulo 2 ; en effet, la
division de 16 par 2 donne pour reste 0 et
la division de 5 par 2 donne pour reste 1.
Revenons au cas général :
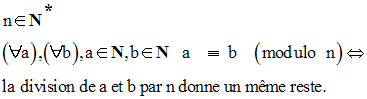
Cette relation dans N est dite congruence. Notons la R.
Montre que R est une relation d’équivalence sur N.
On donne le cas particulier n = 3.
a étant un entier naturel quelconque, la classe d’équivalence C(a) est définie par :
{x, x entier naturel tel que x congru à a (modulo 3)} est notée :
Trouve toutes les classes d’équivalence. L’ensemble de toutes ces classes est notée N / 3.

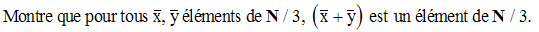

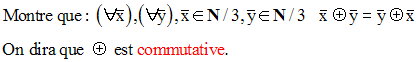
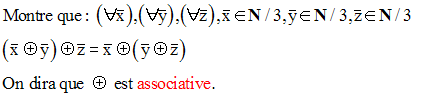
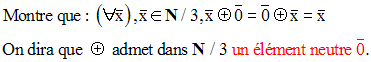
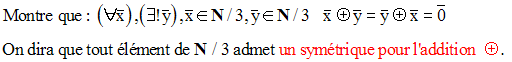
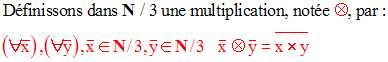




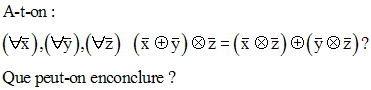
Résous dans N / 5, les équations suivantes :
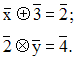
Solution
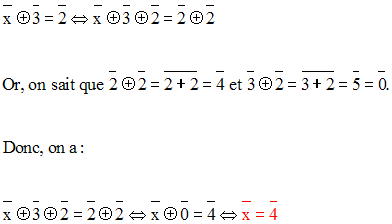

Donc, on a :
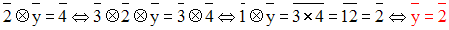
Dans N / 4 on pose :
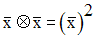
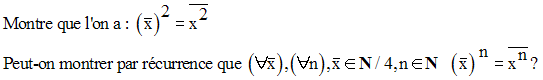
Solution
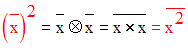
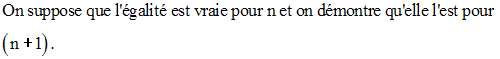
On a :
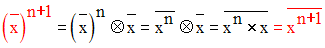
Résous dans N / 5 les équations suivantes :
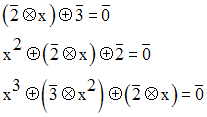
Solution

On a :
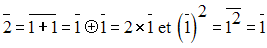
L’équation peut donc s’écrire :
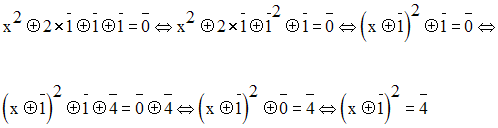
Pour simplifier le tableau, on a indiqué les classes d'équivalence par des chiffres en caractères gras.
| Ä | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
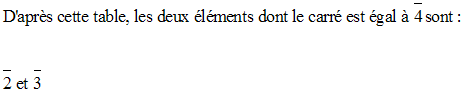
Donc, on peut écrire :
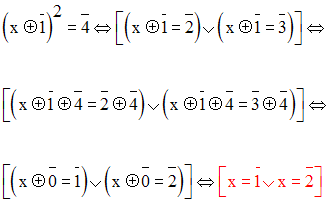
Remarque importante :
Dans plusieurs ouvrages de mathématiques et même dans des
épreuves de baccalauréat,
par abus d’écriture,
on remplace les signes :

respectivement par + et × (ou .).
Il faut donc garder à l’esprit que dans ce cas les
opérations + et . définies dans N / n
sont différentes
des additions et multiplication naturelles définies dans N.
5)
Généralisation
Dans tout ce qui précède, on a défini la congruence dans N.
Cette définition s’applique également à l’ensemble Z des entiers relatifs.
Ainsi on a :
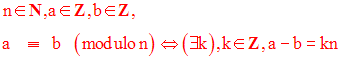
Les classes d’équivalence sont :
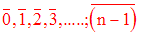
L'ensemble des classes d'équivalence sera défini comme suit :
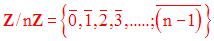
On peut également définir les mêmes lois de composition
interne que ci-dessus.
Ces lois auront les mêmes propriétés dans Z
/ nZ : commutativité,
associativité,
existences d’éléments neutres
pour chacune des lois, symétrisation des
éléments de Z / nZ.
De la définition de la congruence et des propriétés qui en découlent, montre les théorèmes suivants :

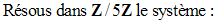
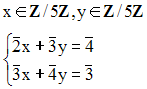
Solution
Les addition et multiplication sont définies dans l'ensemble des classes d'équivalence.
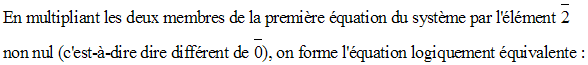

Or, on a :
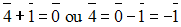
Donc,
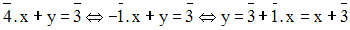
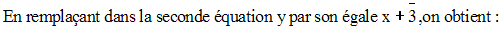
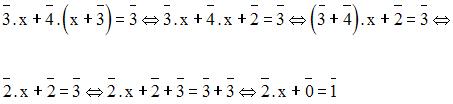
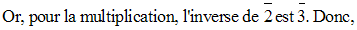
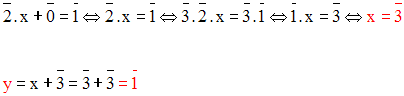
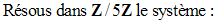
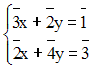
Solution
En additionnant membre à membre, on obtient :
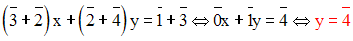
En remplaçant, dans la première équation, y par sa valeur trouvée, on
obtient :
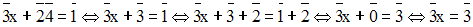
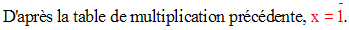
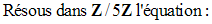
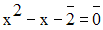
Solution
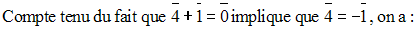
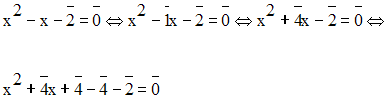
Or,
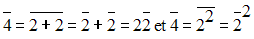
Donc,
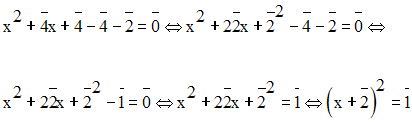
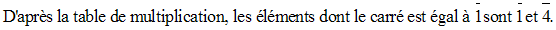
Donc, on peut écrire :
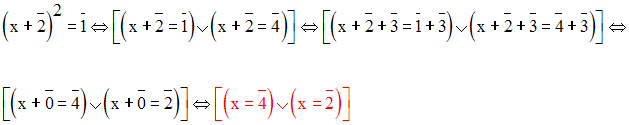
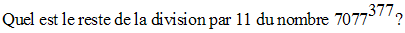
Solution
On a :
7077 = 11 ´ 643 + 4
Donc,
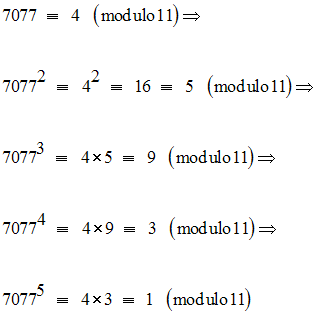
A partir de ce moment, les restes des divisions par 11 des
puissances successives de 7077,
se reproduisent périodiquement
et l’on a, relativement au module 11 :
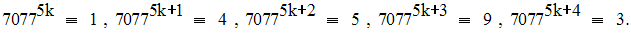
On a, 377 = 5 ´ 75 + 2.
Donc,
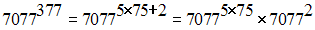
Par conséquent, on obtient :
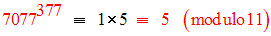
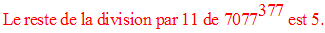
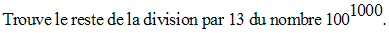
Solution
Relativement au module 13, on a :
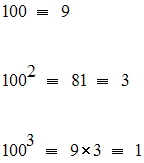
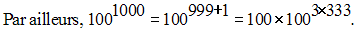
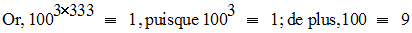
Donc, on a :
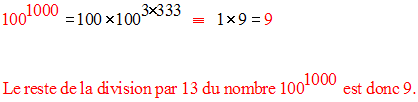
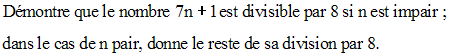
Solution
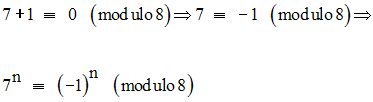
Ainsi, on a :
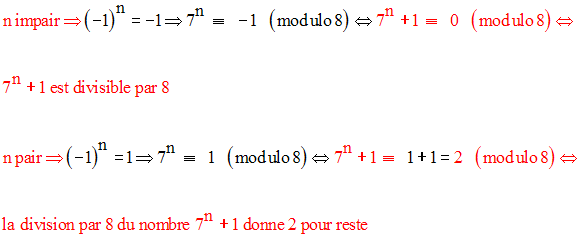
fin de la troisième partie