NOTIONS ELEMENTAIRES DE LA THEORIE DES ENSEMBLES ET DE
TOPOLOGIE
4ème partie
1- Intervalles
Soit E un ensemble ordonné par une relation d’ordre, notée ≤.
La relation d’ordre strict qui en découle sera notée <.
Soit deux éléments a, b de E tels que a ≤ b.
On appelle intervalle fermé d’origine a et d’extrémité b, l’ensemble des éléments x de E tels que a ≤ x ≤ b.
On note :

Soit maintenant a < b.
On appelle intervalle ouvert d’extrémités a et b, l’ensemble des éléments x de E tels que a < x < b.
On note :

On appelle intervalle semi-ouvert à droite (ou semi-fermé à gauche) d’origine a et d’extrémité b, l’ensemble des éléments x
de E tels que a ≤ x < b.
On note :

On appelle intervalle semi-ouvert à gauche (ou semi-fermé à droite) d’origine a et d’extrémité b, l’ensemble des éléments x
de E tels que a < x ≤ b.
On note :

2- Majorants et minorants
Soit (E , ≤) un ensemble ordonné et A une partie non vide de E.
On notera d’abord que les écritures x ≤ y et y ≥ x sont synonymes.
S’il existe un élément a de E tel que :

alors on dira que a est un majorant de A.
Dans ce cas on dira que A est majorée.
S’il existe un élément b de E tel que :

alors on dira que b est un minorant de A.
Dans ce cas on dira que A est minorée.
On dira que la partie A de E est bornée si et seulement si elle est simultanément minorée et majorée.
Exemples :
On a vu que N est ordonné par la relation de divisibilité notée | .
Soit une partie A = {a , b} de N, avec a et b différents.
Pour la relation d’ordre | , tout multiple commun à a et b est un majorant de A et tout majorant de A est
multiple commun à a et b.
De même, tout diviseur
commun à a et b est un minorant de A
et tout minorant de A est
un
diviseur commun à a et b.
Donc A est bornée pour cette relation d’ordre.
Soit (R , ≤) l’ensemble des nombres réels ordonné.
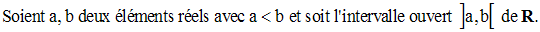

Donc pour la relation d’ordre ≤ , b est un majorant de ]a , b[.
De même, a est un minorant de ]a , b[.
Donc ]a , b[ est borné.
3- Elément maximum et élément minimum
Soit (E , ≤) un ensemble ordonné et A une partie non vide de E.
S’il existe un majorant a de A vérifiant :
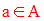
alors on dira que a est élément maximum de A . Il sera noté :
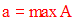
S’il existe un minorant b de A vérifiant :
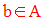
alors on dira que b est élément minimum de A . Il sera noté :
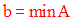
Exercice
Montre que si A possède un élément minimum et un élément maximum, alors ces éléments sont uniques.
Pour la relation d’ordre naturel ≤ dans N, on a les deux propriétés qu’il est bon de retenir :
Toute partie non vide de N admet un élément minimum :
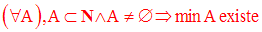
Toute partie non vide et majorée de N admet un élément maximum :
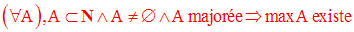
4- Borne supérieure et borne inférieure
Soit (E , ≤) un ensemble ordonné et A une partie non vide de E.
Si l’ensemble M des majorants de A n’est pas
vide et admet un élément minimum, ce dernier est alors
nommé
borne supérieure de A et se note :
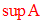
On a donc :
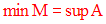
Si l’ensemble N des minorants de A n’est pas
vide et admet un élément maximum, ce dernier est alors
nommé
borne inférieure de A et se note :
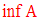
On a donc :
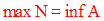
Lorsqu’ils existent, infA et supA sont uniques.
Lorsqu’un majorant de A appartient à A, il est simultanément maxA et supA.
De même lorsqu’un minorant de A appartient à A, il est simultanément minA et infA.
Exemples :
Soit N ordonné par la relation de divisibilité et soit A = {a , b} une partie non vide de N.
L’ensemble M des majorants de A est l’ensemble des
multiples communs à a et b.
M admet un élément minimum qui est
le plus petit multiple commun à a et b, noté
ppmc(a,b).
Donc on a :
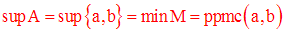
L’ensemble N des minorants de A est l’ensemble des
diviseurs communs à a et b.
N admet un élément maximum qui est
le plus grand diviseur commun à a et b, noté
pgdc(a,b).
Donc on a :
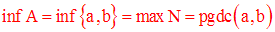
Exemple :
Soit (R , ≤) l’ensemble des nombres réels ordonné par la relation ≤ .
Soit l’intervalle A = ]0 , 1[. A est une partie non vide de R.
L’ensemble M des majorants de A est l’intervalle :
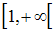
De plus min M = 1 ; donc sup A = 1.
Aucun élément de M n’appartienne à A ; donc A ne possède pas un élément maximum.
Exercice
La partie A de R telle que définie immédiatement
ci-dessus est-elle minorée ?
Possède-t-elle un minimum ?
Exercice
Soit P(E) l’ensemble des parties d’un ensemble E,
ordonné par la relation d’inclusion et soit
F = {A , B} une partie de P(E).
L’ensemble M des majorants de F est défini par :
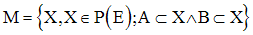
Montre que l’on a :
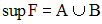
Définis par compréhension l’ensemble N des minorants de F et montre que l’on a :
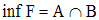
5- Topologie de la droite réelle R
R étant l’ensemble des nombres réels.
On dit qu’un sous-ensemble A de R est
ouvert s’il est
vide ou si, pour tout
x élément de A, il existe au moins
un intervalle ouvert de R
contenant x et contenu dans A.
Autrement dit, un ouvert de R est un ensemble qui est une réunion d’intervalles ouverts.
De cette définition découlent immédiatement les propriétés suivantes :
Toute réunion (finie ou non) d’ouverts de R est un ouvert de R
Toute intersection finie d’ouverts est un ouvert de R
R et l’ensemble vide sont des ouverts.
Si on note O l’ensemble des ouverts de R, alors on dira que O est une topologie de la droite réelle R.
Exemples :
1)
Tout intervalle ouvert est un ensemble ouvert.
Démontrons cette assertion.
Soit un intervalle ouvert quelconque ]a , b[ inclus dans R.
Soit un élément x quelconque de cet intervalle.
On a donc a < x < b.
Que peux-tu dire de l’intervalle défini par :
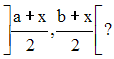
En déduis que ]a , b[ est ouvert.
2)
La réunion des intervalles ouverts ]n , n+1[ où n est un élément de Z est un ensemble ouvert.
3)
Soit dans R l’ensemble défini par :
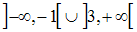
Montre que cet ensemble est un ouvert.
4)
Soit I = [a , b] un intervalle fermé de R. Montre que I n’est pas un ouvert.
Montre également que tout intervalle semi-ouvert n’est pas un ouvert.
Remarque importante
Il est faux que l’intersection d’une infinité d’ouverts de R soit toujours un ouvert.
Par exemple, on donne les intervalles ouverts définis par :
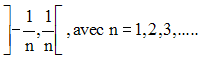
Quel est l’intersection de tous ces ouverts ?
Est-elle un ouvert ?
Exemple :
Soient les intervalles de R définis par :
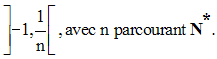
Montre que leur réunion est un ouvert et que leur intersection ne l’est pas.
On dit qu’un sous-ensemble A de R est fermé lorsque sa partie complémentaire :
De chacune des trois propriétés ayant défini ci-dessus une topologie de R découle donc les propriétés suivantes :
Toute intersection, finie ou non de fermés est un fermé
Toute réunion finie de fermés est un fermé ;
R et l’ensemble vide sont des fermés.
Exemple :
Montre que tout intervalle fermé de R est un fermé.
Remarque importante
Un ensemble peut n’être ni un ouvert, ni un fermé ; c’est le cas, par exemple, de l’ensemble Q des nombres rationnels.
Voisinage d’un point réel
On appelle voisinage d’un point x de R tout sous-ensemble V de R contenant au moins un ouvert contenant x.
Autrement dit, V est voisinage de x élément de R si et seulement si V contient un intervalle ouvert contenant x.
Exemple :
Tout ensemble ouvert A est voisinage de
chacun de ses éléments.
Réciproquement, tout ensemble A qui est
voisinage de chacun de ses éléments est une réunion d’intervalles ouverts,
donc est ouvert.
Exercice
Soient x et y deux réels distincts quelconques et supposons que x < y.
Montre qu’il existe un voisinage Vx de x et un voisinage Vy de y tels que :
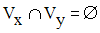
Remarque
Le sens mathématique de la notion de voisinage d’un
point réel diffère de celui du langage courant.
En effet ce point réel peut
posséder plusieurs voisinage dont R.
6- Distance dans R
Soit E un ensemble quelconque.
E est dit espace métrique si et seulement s’il existe une application, notée
d(x , y), de E × E = E2 dans R+ possédant les propriétés suivantes :
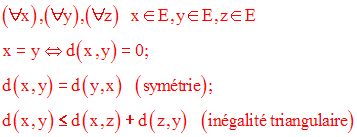
L’application d est appelée distance sur E et la quantité positive d(x , y) est appelée distance des points x et y.
Exercices
1)
Montre que l’application f de R2 dans R+ définie par :
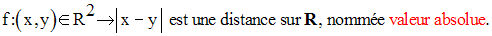
donc que R est un espace métrique.
2)
Montre que si d est une distance sur E, alors pour tous x, y, z éléments de E :
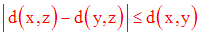
Dans tout ce qui suit on prendra
E = R et comme distance sur R,
la valeur absolue telle que définie
ci-dessus.
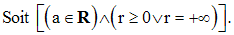
On appelle boule ouverte (resp : boule fermée) de R, de centre a, de rayon r,
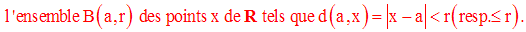
On appelle sphère de centre a
et de rayon r ≥ 0 la partie de R notée
S(a , r) dont les éléments sont les réels x
tels que
d(a , x) = | x –a | = r.
Ainsi, une boule ouverte (resp.
boule fermée) de l’espace métrique R muni de la distance d définie
ci-dessus
n’est autre qu’un intervalle ouvert (resp.
intervalle fermé).
La sphère de entre a et de
rayon r n’est autre que l’ensemble pair :

L’ensemble O des intervalles ouverts de R muni de la distance d : d(x , y) = | x – y | vérifie les trois propriétés suivantes :
L’intersection finie d’intervalles ouverts est un intervalle ouvert ;
La réunion finie ou non d’intervalles ouverts est un ouvert ;
R et l’ensemble vide sont des intervalles ouverts.
On dira que O est une topologie de R associée à la distance d.
Soient A, B deux parties quelconques de R.
On appelle distance de A et B,
notée d(A , B), la
borne inférieure de l’ensemble des réels positifs d(x , y) = | x – y
|
quand x, y parcourent respectivement A et B.
Donc on a :
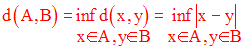
Si A = {a}, cette distance se nomme distance du point a à l’ensemble B et est notée : d(a , B).
Propriété
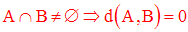
Remarque
d(A , B) n’est pas une distance sur l’ensemble des parties de R.
Par exemple d(A , B) = 0 n’implique pas A = B.
Diamètre d’une partie de R
On appelle diamètre d’une partie A de R, la borne supérieure, notée :

de l’ensemble des distances d(x , y) = | x – y | , x et y parcourant tous les éléments de A.
On admettra que A est bornée lorsque son diamètre est un réel positif fini. Dans le cas contraire on posera :
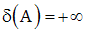
Exercice
Montre que tout intervalle I de R, fermé ou ouvert, de rayon r, a un diamètre égal à :
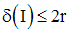
7- Points d’accumulation, points intérieurs et extérieurs, adhérence
Si A est un sous-ensemble de R, un point
a appartenant à R est dit point
d’accumulation de A
si et seulement si
tout voisinage de a contient au moins
un élément de A différent de a.
On admettra sans démonstration que
si a est un point d’accumulation de A,
alors il existe dans
tout voisinage de a
une infinité de points de A différents de a.
Remarque importante :
Un point d’accumulation d’une partie A de R n’appartient pas nécessairement à A.
Exercices
1)
Soit A la partie de R définie par :
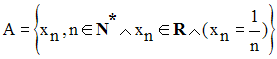
Montre que 0 est point d’accumulation de A.
2)
Montre que 0 et 1 sont des points d’accumulation de ]0, 1[.
On admettra sans démonstration
que toute partie fermée de R contient ses points d’accumulation.
Inversement, toute partie de R contenant ses points d’accumulation
est fermé.
Soit A une partie de R. Un point b appartenant à A est dit isolé si et seulement si b n’est pas un point d’accumulation de A.
Autrement dit, x est un point de A possédant au moins un voisinage V tel que :
Exercice
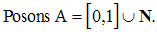
Montre que les points isolés de A sont les entiers naturels largement supérieurs à 2.
Si A est un sous-ensemble de R, un point
a appartenant à R est dit point
intérieur à A s’il existe au moins
un
intervalle ouvert de centre a, inclus dans A.
L’ensemble des points intérieurs à A se nomme intérieur de A et se note :
Exercices
1)
Montre que l’on a, pour toute partie de R :
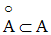
2)
Montre que l’on a, pour toutes parties A, B de R :
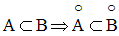
3)
On donne un intervalle I = [a , b] de R.
Trouve l’intérieur de I.
4)
Montre que si une partie A de R est un ouvert, alors :
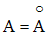
5)
Montre que pour toute partie A de R, l’intérieur de A est un ouvert.
Propriété
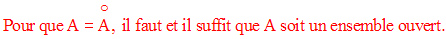
Remarque
Si A = {a , b} est un ensemble de deux réels quelconques a et b, alors l’intérieur de A est l’ensemble vide.
On dit qu’un point a de R est extérieur à une partie A de R s’il est intérieur au complémentaire R – A de A.
L’intérieur de (E – A) se nomme extérieur de A.
Donc l’extérieur de A est un ouvert.
On dit qu’un point a de R est adhérent à une partie A de R si tout voisinage de a rencontre A.
L’ensemble de tous les points adhérents à A se nomme adhérence de A et se note :
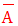
Exercices
1)
Montre que pour toute partie A de R, l’adhérence de A est un fermé.
2)
Montre que pour toute partie A de R, l’adhérence de A est le complémentaire de l’extérieur de A ; c’est-à-dire :
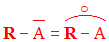
Propriété
Pour qu’une partie A de R soit égale à son adhérence, il faut et il suffit que A soit un fermé.
Un point a de R est dit frontière d’une partie A de R s’il est adhérent à la fois à A et à R – A.
L’ensemble des points frontières de A se nomme la frontière de A et se note Fr(A).
Ainsi, on a :
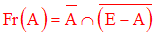
Exercice
Montre que pour toute partie A de R :
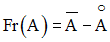
fin de la quatrième partie