---

 

NOTIONS ELEMENTAIRES DE LA THEORIE DES ENSEMBLES ET DE TOPOLOGIE

 

2ème partie

 

---

 

 

 

 

1. Produit cartésien de deux ensembles

 

 

A partir de deux objets mathématiques a et b, on peut former un nouvel objet noté (a,b) et appelé couple.

 

a sera dit premier élément du couple et b sera dit second élément du couple.

 

Deux couples (a,b) et (a’,b’) sont égaux si et seulement si a = a’ et b = b’.

 

On a la tautologie suivante :

 

 

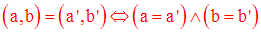
Ainsi (a,b) est généralement différent de (b,a) ; l’égalité n’a lieu que si a = b.

 

Soient deux ensembles quelconques E, F.

 

 

Exemples

 

 

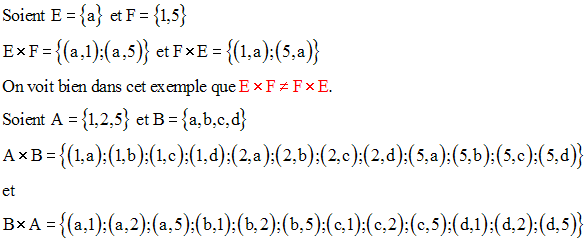
Le produit cartésien n’est pas commutatif.

 

Cas particulier

 

Si E est égal à F alors on écrira :

 

 

 

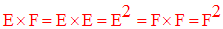
Propriété

 

 

 

 

 

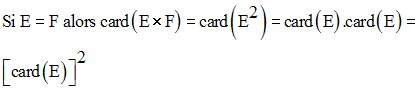
2. Relation d’un ensemble vers un ensemble

 

Soient deux ensembles quelconques E et F.

 

Une relation entre un élément x de E et un élément y de F, notée f, exprime une propriété mathématique vérifiée
par le couple (x,y) de E×F.

 

On dira que f est une relation de E vers F. E est appelé ensemble de départ ou source et F, ensemble d’arrivée
ou but.

 

Si le couple (x,y) vérifie f alors x sera appelé antécédent de y par f et y sera appelé image de x par f.

On écrira y = f(x).

 

L’ensemble des couples (x,y) vérifiant f appartient à E×F et sera appelé graphe de la relation f.

 

 

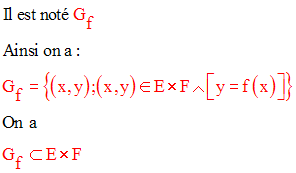
Si E = F alors on dira que f est une relation dans E ou dans F.

 

La relation f de E vers F peut être définie de trois manières différentes :

-         par son graphe ;

-         par son schéma sagittal ;

-         par son schéma cartésien.

 

Définition de f par son schéma sagittal

 

On représente la source E et le but F par des courbes fermés renfermant les éléments ; ces courbes sont les
diagrammes de Venn.

Ensuite pour chacun des couples (x,y) vérifiant f on trace une flèche allant de x vers y.

 

Le schéma obtenu est appelé schéma sagittal de f.

 

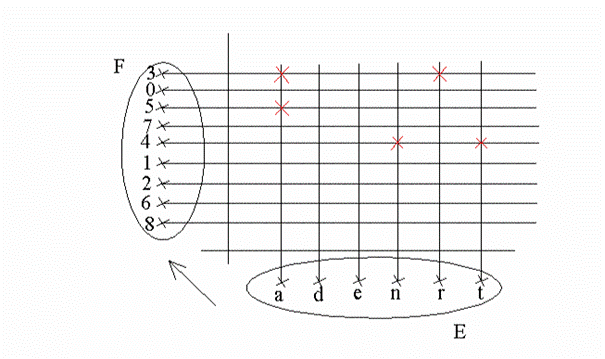
Exemple

 

 

 

Son schéma sagittal est représenté par la figure ci-dessous.

 

 

 

Il peut exister des éléments de E qui n’ont pas d’image par f ; par exemple d et e.

Comme également il peut exister des éléments de F qui n’ont pas d’antécédent par f ; par exemple 0, 7, 2.

 

Définition de f par son schéma cartésien

 

On utilise toujours les diagrammes de Venn.

 

Mais cette fois les éléments sont alignés horizontalement et verticalement.

 

De chaque élément aligné à l’horizontale part une droite verticale et de chaque élément aligné à la verticale
part une droite horizontale.

 

Tout couple de E×F vérifiant f sera ainsi représenté par un point qui est l’intersection d’une droite verticale et
d’une droite horizontale.

 

Pour lever toute ambiguïté, une petite flèche est placée à l’angle inférieur gauche du schéma indiquant
explicitement les source et but de la relation f.

 

Pour notre exemple, la figure ci-dessous représente le schéma cartésien de f.

 

 

 

Soient deux relations f et g définies par leurs données :

(E, F, f) et (E’, F’, g).

 

On dira que f et g coïncident  ou sont égales si et seulement si :

E = E’ ;

F = F’ :

G_f  = G_g .

 

 

 

3. Relation réciproque

 

On donne la donnée d’une relation f :

 

 

 

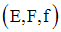
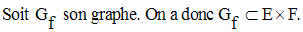
On appelle relation réciproque de f la relation notée :

 

 

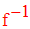
et ayant pour source F et pour but E.

 

 

 

 

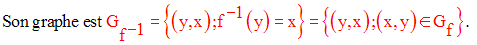
Exemple

 

 

Soit E = {2,5,4,10,3} et g la relation binaire sur E définie par :

 

x divise y

 

Avec cette donnée, on peut définir par extension le graphe G_g de g ; on a :

 

G_g = {(2,2) ; (2,4) ; (2,10) ; (4,4) ; (5,5) ; (5,10) ; (10,10) ; (3,3)}

 

Par ailleurs, on peut définir la relation binaire g^–1  réciproque de g par :

 

x est multiple de y

 

Son graphe G_g^{– 1}  sera :

 

G_g^{– 1} = {(2,2) ; (4,2) ; (10,2) ; (4,4) ; (5,5) ; (10,5) ; (10,10) ; (3,3)}

 

 

 

4. Application d’un ensemble dans un autre

 

 

On dira que f est une application de E dans F si et seulement si tout élément de la source E possède par f
une image et une seule dans le but F.

 

Ainsi, s’il existe au moins un élément de la source E n’ayant pas d’image par f, alors f n’et pas une application.

 

De même, s’il existe au moins un élément de la source E ayant deux images ou plus dans le but F,
alors f n’est pas une application.

 

Si E = F alors on dira que f est une application dans E ou dans F.

 

L’application f dans E qui à tout élément x de E applique f(x) = x est appelée application identique de E
et est notée :

 

 

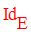
Ainsi on a :

 

 

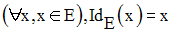
Le graphe de Id_E n’est autre que l’ensemble des couples (x , y) de E × E = E² tels x = y.
On l’appelle diagonale de E² .

 

Exemples

 

Parmi les relations suivantes f, g, h, de E = {1,2,3} vers F = {a,b,c,d} et définies par leurs graphes respectifs:

 

 

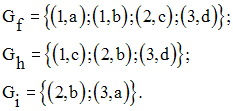
f n’est pas une application car l’élément 1 de la source E possède deux images distinctes a et b dans le but F ;
h est une application car tout élément de la source E possède une image et une seule dans le but F ;
i n’est pas une application car l’élément 1 de la source ne possède aucune image dans le but F.

 

Remarque importante :

 

Peu importe que les éléments du but (ensemble d’arrivée) aient ou non des antécédents, par la relation,
dans la source (ensemble de départ) ; pour que la relation soit une application, il faut et il suffit que
tout élément de la source ait une image et une seule dans le but.

 

 

 

 

 

Pour démontrer que tous les termes u_n de cette suite numérique vérifient une propriété P,
on utilise ce que l’on appelle la démonstration par récurrence.

 

La méthode est la suivante :

 

D’abord on constate que la propriété P est vérifiée pour le rang 0, c’est-à-dire u₀ vérifie P,
et qu’elle est également vérifiée pour le rang 1, c’est-à-dire u₁ vérifie P.

 

Ensuite on suppose que P est vérifiée pour le rang (n – 1), c’est-à-dire u_n-1 vérifie P et enfin
on démontre qu’elle est vérifiée pour le rang n, c’est-à-dire u_n vérifie P.

 

Exemple

 

 

 

 

 

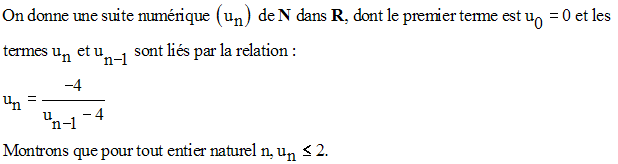
5- Injection, surjection et bijection

 

Soit f une application de E dans F.

 

On note Im(f) l’ensemble des images des éléments de E par f.

 

 

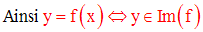
Il est évident que l’on ait l’inclusion suivante :

 

 

 

 

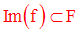
On dira que l’application f est une injection (ou une application injective) si et seulement si tout
élément du but F possède par f et dans la source E au plus un antécédent.

 

 

 

 

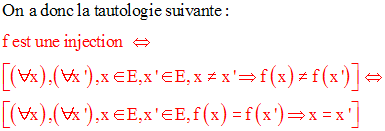
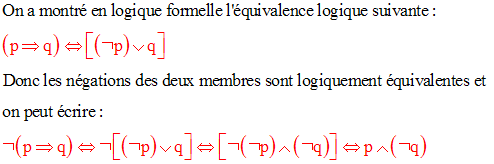
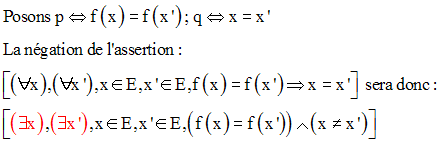
Ainsi on a la tautologie suivante :

 

 

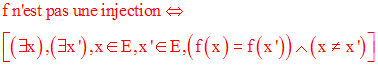
Pour montrer qu’une application f de E dans F n’est pas une injection, il suffit de montrer l’existence de
deux éléments distincts x et x’ de E tels que f(x) soit égale à f(x’).

 

 

Exercices

 

 

 

 

Soit f  l’application dans R définie par :

 

 

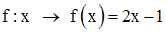
f est-elle injective ?

 

Solution

 

g n’est pas une application dans R car l’élément 0 de R n’aucune image par g dans R.

 

Si g est une relation de R^*dans R, alors elle est partout définie dans R^*,
c’est-à-dire tout élément de R^*possède par g une image dans R.

 

De plus, on a :

 

Cette image est unique.

 

Donc g est une application de R^* dans R.

 

 

 

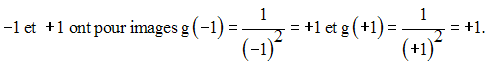
Donc, on a :

 

 

 

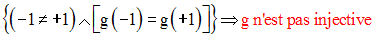
Soit f  l’application dans R définie par :

 

 

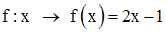
On a, pour tout x et pour tout x’ éléments de R :

 

 

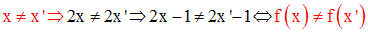
Donc, f est une injection.

 

 

 

On dira que l’application f est une surjection (ou une application surjective) si et seulement si tout
élément du but F possède par f et dans la source E au moins un antécédent.

 

 

On sait que :

 

 

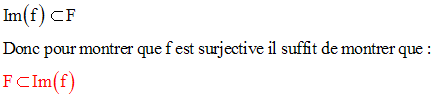
Exercice

 

On donne f une relation dans R définie par :

 

 

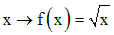
1- f est-elle une application dans R ?

 

 

Solution

 

1-

 

Tout nombre réel strictement négatif n’a aucune image par f ; donc f n’est pas une application dans R.

 

On suppose pour la suite que f  est une relation dans R⁺.

 

Dans ce cas, f est partout définie dans R⁺ : tout réel largement positif possède une image par f dans R⁺.

 

De plus, on a :

 

 

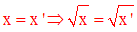
Cette image est unique.

 

Donc f est une application dans R⁺.

 

On a, pour tout x et pour tout x’ éléments de R⁺ :

 

 

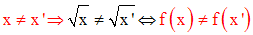
Donc, f est une injection.

 

On sait que :

 

 

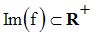
On démontre que :

 

 

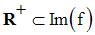
Pour tout réel y largement positif, il existe au moins un réel largement positif x tel que :

 

 

 

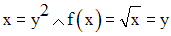
y appartient donc à Im(f).

 

 

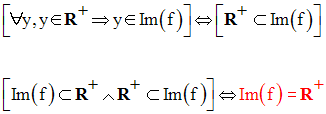
Conclusion : f est surjective.

 

 

 

On dira que l’application f est une bijection de E sur F (ou une application bijective) si et seulement si f est
une application ET tout élément du but F possède par f et dans la source E un antécédent et un seul.

 

Ainsi une application f est bijective si et seulement si elle est injective et surjective.

 

Si E = F on dira que f est une bijection sur E ou sur F.

 

Exemple :

 

L’application f dans R⁺ définie par :

 

 

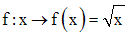
a été étudiée ci-dessus.

 

On a démontré qu’elle est à la fois injective et surjective.

 

Donc f est une bijection sur R⁺.

 

 

Exercices

 

1- Parmi les applications suivantes lesquelles sont bijectives ?

 

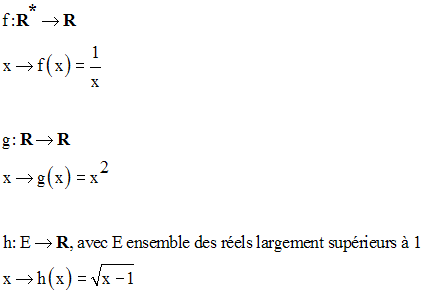
E est l’ensemble des réels largement supérieurs à 1

 

 

2-

 

On donne une application i de E dans R définie par :

 

 

Quelles sont les parties non vides de R auxquelles E peut s’identifier pour que i soit une bijection ?

 

 

 

3-

 

Soient E, F deux ensembles quelconques.

 

On donne une application injective f de E dans F.

 

On pose Im(f), l’ensemble des éléments de F possédant, par f, des antécédents dans E.

 

Montre que f est une bijection de E sur Im(f).

 

Solution

 

1-

 

 

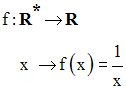
f est partout définie dans R^* ; donc, tout élément x de R^* possède par f une image dans R.

 

Par ailleurs, on a :

 

 

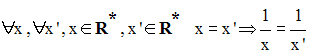
Donc, l’image, par f, de tout élément x de R^* est unique.

 

Conclusion : f est une application de R^* dans R.

 

 

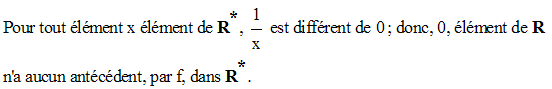
On a ainsi :

 

 

 

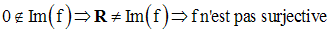
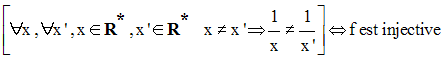
f étant injective et n’étant pas surjective, n’est pas une bijection de R^* sur R.

 

 

 

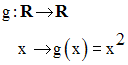
g est partout définie dans R; donc, tout élément x de R possède par g une image dans R.

 

Par ailleurs, on a :

 

 

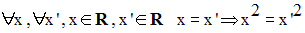
Donc, l’image, par g, de tout élément x de R est unique.

 

Conclusion : g est une application dans R.

 

Tout élément y, strictement négatif, de R n’a aucun antécédent, par g, dans R, car il n’existe aucun
réel x tel que x² est égal à y, avec y strictement négatif.

 

Par conséquent, R^–  n’est pas inclus dans Im(g), et ainsi, Im(g) est différent de R.

 

Im(g) étant différente de R, g n'est donc pas surjective.

 

–1 et +1 ont pour image g(–1) = g(+1) = +1.

 

Donc, on a :

 

 

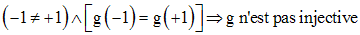
g n’étant pas injective et n’étant pas surjective, n’est pas une bijection dans R .

 

 

 

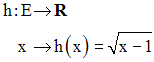
h est partout définie dans E; donc, tout élément x de E possède par h une image dans R.

 

Par ailleurs, on a :

 

 

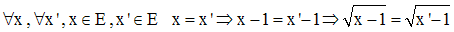
Donc, l’image, par h, de tout élément x de E est unique.

 

Conclusion : h est une application de E dans R.

 

 

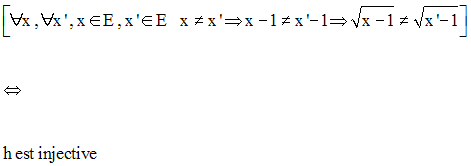
Soit y un élément quelconque de R.

 

On a :

 

 

 

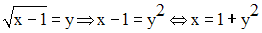
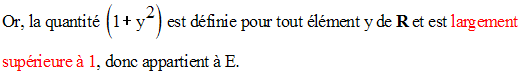
Conclusion :

 

Pour tout y élément de R, il existe au moins un élément x appartenant à E tel que h(x) = y.

 

R est donc une partie de Im(h).

 

Or, on sait que Im(h) est une partie du but R.

 

 

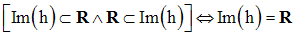
Im(h) étant égal à R, h est surjective.

 

h étant simultanément injective et surjective, est une bijection de E sur R.

 

 

2-

 

Les parties non vides de R auxquelles E et F peuvent respectivement  s’identifier pour que
i soit une bijection sont :

 

 

 

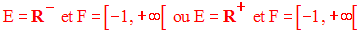
3-

 

Soient E, F deux ensembles quelconques.

 

On donne une application injective f de E dans F.

 

Soit Im(f) l’ensemble des éléments de F possédant des antécédents, par f, dans E.

 

f étant une application de E dans F, tout élément x de E possède une image et une seule dans F et
cette image appartient à Im(f).

 

f étant une injection, tout élément de Im(f) possède au plus un antécédent dans E.

 

Conclusion :

 

tout élément x de E  possède, par f, une image et une seule dans Im(f) et tout y de Im(f) possède,
par f, un antécédent et un seul dans E.

 

Donc f est une bijection de E sur Im(f).

 

Remarque :

 

Cette propriété est très importante ; souvent on l’utilise dans les problèmes pour démontrer
qu’une application ou une fonction est bijective.

 

 

Propriétés

 

Si f est une bijection de E sur F, alors sa réciproque f ^-1 de F vers E est une bijection de F sur E.

 

 

Exercice

 

Dans ce cas a-t-on :

 

 

 

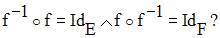
Considérons le cas où  E = F ; alors f est appelée permutation de E (ou de F).

 

Exemple :

 

Soit l’ensemble E = {a, b, c}.

 

Soit (E, E, f) la donnée d’une application dans E définie par son graphe :

 

 

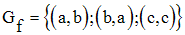
Tout élément de E possède par f une et une seule image.

 

Tout élément de E possède par f un et un seul antécédent.

 

Donc f est une bijection sur E ou encore une permutation de E.

 

L’application identique Id_E  définie par la diagonale :

 

 

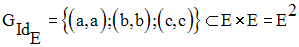
est également une permutation de E.

 

 

f étant une permutation de E, si de plus f = f ^-1 alors on dira que f est une involution.

 

Exemple :

 

 

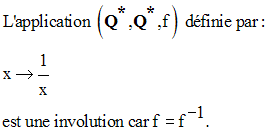
Il est facile de démontrer que f est bijective.

 

On démontre ensuite qu’elle est une involution.

 

En effet, on a :

 

 

 

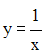
Or, x et y appartenant à Q^*, sont différents de 0 et on peut écrire :

 

 

 

 

 

 

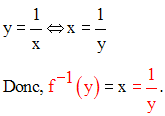
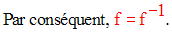
6- Composée de deux applications

 

On donne deux applications f et g définies respectivement par leurs données :

 

(E, F, G_f ) et (F, G, G_g )

 

On a donc f une application de E dans F et g une application de F dans G.

 

On remarque bien que le but de f est la source de g.

 

De plus, on a :

 

Dom(g) = F

 

En effet, si on suppose que Dom(g) est différent de F, alors il existerait un élément de F qui,
n’appartenant pas à Dom(g), n’aurait aucune image, par g, dans G ; donc g ne serait pas une
application de F dans G.

 

Ce qui est contraire à l’hypothèse.

 

 

A tout élément x de E correspond une seule image y = f(x) dans F.

 

A cet élément y de F correspond une seule image z = g(y) dans G.

 

Par suite, à tout x de E correspond une unique image z dans G qu’on note :

 

g[f(x)]

 

On définit ainsi une application de E dans G appelée composée de f et g et notée :

 

 

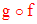
qui se lit  « g rond f » ou encore « f suivie de g ».

 

On a donc :

 

 

 

 

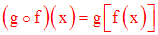
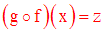
Exemples :

 

1-

 

 

Soit f une application de E dans F définie par son graphe :

 

 

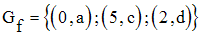
Soit g une application de F dans G définie par son graphe :

 

 

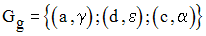
On a :

 

 

Donc,

 

 

 

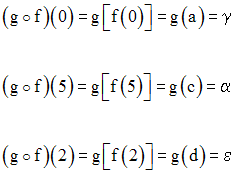
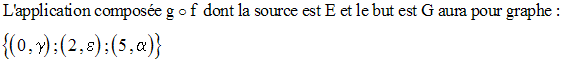
On remarque que :

 

Dom(g) = F

 

 

2-

 

 

 

 

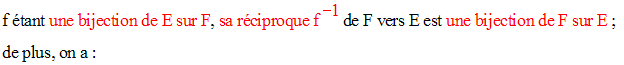
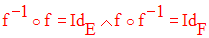
Propriétés

 

Il est évident que la composition des applications n’est pas commutative :

 

 

 

 

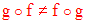
La composée de deux injections (resp. surjections) est une injection (resp. surjection).

 

Démonstration

 

 

 

 

 

 

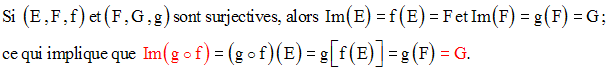
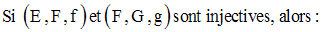
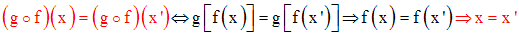
La composée de deux bijections est une bijection.

 

 

 

Soient trois applications quelconques f, g, h définies par leurs données :

 

(E, F, f) ; (F, G, g) ; (G, H, h)

 

On a :

 

 

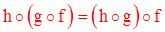
On dira que la composition des applications est associative.

 

 

 

On donne deux bijections quelconques f et g définies respectivement par leurs données :

 

 

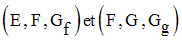
On a l’égalité suivante :

 

 

 

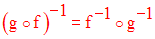
Exercice

 

On donne l’application (Z, N, f) définie par :

 

 

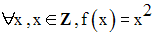
On donne également une application (N, N, g)  définie par :

 

 

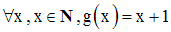
Solution

 

f est partout définie dans Z ; de plus, tout élément de Z possède, par f, une image et une seule dans N.

Donc f est une application de Z dans N.

 

g est partout définie dans N ; de plus, tout élément de N possède, par g, une image et une seule dans N.

Donc g est une application dans N.

 

 

Soit x un élément quelconque de Z.

 

On a :

 

 

 

 

 

 

 

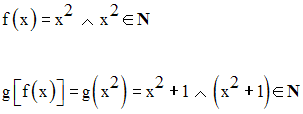
7- Bijection et extension de la notion de cardinal d’un ensemble

 

On a déjà défini le cardinal d’un ensemble fini.

 

 

Dans ce paragraphe on étendra cette notion à des ensembles infinis, grâce à la notion de bijection.

 

Deux ensembles quelconques E, F sont dits équipotents si et seulement s’il existe au moins une bijection
de E sur F ou de F sur E.

 

Propriété

 

Un ensemble X est dit fini si et seulement s’il est équipotent à une partie non vide finie de N.

On dira aussi que X est fini dénombrable.

 

 

Attachons à tout ensemble X un nouveau objet mathématique appelé cardinal de X et noté card(X).

 

Soient deux ensembles quelconques E, F.

 

On a l’équivalence logique suivante :

 

 

Si E et F sont finis alors leurs cardinaux sont des entiers naturels et dans le cas de l’équivalence logique
précédente on a : card E = card f = n, n entier naturel.

 

On a donc E et F finis dénombrables.

 

Un ensemble X infini possède un cardinal infini. De plus si X est équipotent à N ou à une partie non vide de N,
alors on dira que X est infini dénombrable.

 

Exemple

 

L’ensemble P des entiers naturels pairs est équipotent à N, P est donc infini dénombrable.

 

En effet il suffit de considérer la bijection f de N sur P définie par f(n) = 2n.

 

Donc card P = card N.

 

Exercice

 

Montre que si I est l’ensemble des entiers naturels impairs, alors I est infini dénombrable et
card I = card P = card N.

 

Propriété

 

 

Exercice

 

De cette dernière propriété, peux-tu déduire que l’ensemble des nombres rationnels Q est équipotent à N,
donc infini dénombrable ?

 

 

Un ensemble X est dit non dénombrable lorsqu’il n’est pas équipotent à N ou à une partie non vide N.

 

Exemple :

 

R est infini non dénombrable et on admet que :

 

 

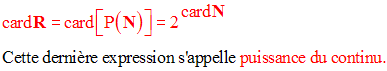
Propriété

 

Tout ensemble équipotent à l’une quelconque de ses parties propres est infini.

 

Exemple :

 

L’application de N dans N - {0} définie par f ( x) = x + 1 est une bijection ;
donc N est équipotent à sa partie propre N - {0} et ainsi N est infini.

 

 

 

 

8- Ensemble de toutes les applications d’un ensemble dans un autre

 

Soient deux ensemble E, F quelconques.

 

L’ensemble de toutes les applications de E dans F est noté : F(E , F)

 

L’ensemble des graphes de toutes les applications de E dans F est une partie de P(E × F), noté :

 

 

 

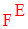
Propriété

 

Si E et F sont non vides et finis, avec card E = e et card F = f, alors on a :

 

 

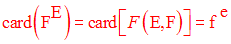
Cette propriété est importante car elle nous permet de calculer le nombre des applications
d’un ensemble dans un autre.

 

Exemple :

 

Soit un ensemble fini E de cardinal 3 et soit F un second de cardinal 2.

Le nombre des applications de E dans F est 2³ = 8 et le nombre des applications de F dans E est 3²  = 9.

 

 

 

Exercices de récapitulation

 

 

1-

 

Soit I une partie de N.

 

Soit P(E) l’ensemble des parties d’un ensemble E.

 

Toute application de I dans P(E) est appelée famille de parties de E, indexée par I. elle se note :

 

 

1.a-

 

Montre que si I et E sont finis de cardinaux respectifs i et e, alors le nombre de familles de parties de E
indexées par I est égal à :

 

 

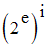
1.b-

 

Dans la suite on suppose que E et I sont quelconques.

 

L’ensemble des éléments x de E tels que x appartiennent à A_i  pour tout i appartenant à I est l’intersection notée :

 

 

 

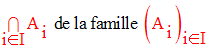
L’ensemble des éléments x de E tels qu’il existe au moins un élément i de I pour lequel x appartient à A_i est
la réunion notée :

 

 

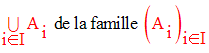
Montre que l’on a :

 

 

 

 

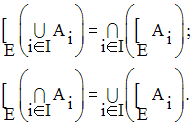
2-

 

On donne un ensemble fini E de n éléments (n entier naturel non nul).

 

On se propose de calculer le nombre de permutations de E.

 

Soit f une bijection quelconque appliquant la partie A = {1, 2, 3, …, n} de N sur E.

 

A toute permutation p de E on peut associer la bijection :

 

 

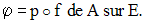
Mais également on a :

 

 

 

 

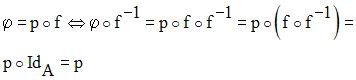
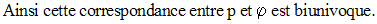
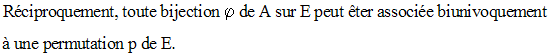
Il existe donc autant de permutations de E que de bijections de A sur E.

 

 

On te donne alors n cases numérotées de 1 à n. On pose un élément quelconque de E dans la première case.
Combien de choix possibles y a-t-il ?

Tu dois trouver n choix possibles.

 

Ce choix étant fait, on pose un élément quelconque parmi les éléments restants de E dans la seconde case.
Combien de choix possibles y a-t-il ?

Tu dois trouver n – 1 = n – (2 – 1) choix possibles

 

Ceci étant fait, on pose un élément quelconque parmi les éléments restants de E dans la troisième case.
Combien de choix possibles y a-t-il ?

Tu dois trouver n – 2 = n – (3 – 1) choix possibles.

 

……………………………………………………………………………………

 

puis, on pose un élément quelconque parmi les éléments restants de E dans la p^ième case.
Combien de choix possibles y a-t-il ?

Tu dois trouver n – (p – 1) choix possibles.

 

……………………………………………………………………………………

 

enfin, combien reste-il de choix possibles pour la n^ième case ?

Tu dois trouver un seul possible puisqu’il ne reste finalement qu’un élément.

 

Quel est au total le nombre de choix possibles ?

Tu dois trouver n × (n – 1) × (n – 2) × (n – 3) ×….× 3 × 2 × 1

 

 

 

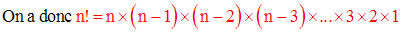
On étendra cette définition à n nul, en posant : 0 ! = 1 ! = 1.

 

A titre d’exemples, 3 ! = 3 × 2 × 1 = 6 et 8 ! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 40320.

 

Applications

 

On te donne E = {a, b, c, e} et A = {1, 2, 3, 4}.

 

Quel est le nombre de bijections de E sur A ?

 

On te donne l’ensemble des voyelles V. Quel est le nombre de permutations de V ?

 

Solution

 

Soit N le nombre de bijections de E sur A.

 

Donc, N = 4 ! = 4 ´ 3 ´ 2 ´ 1 = 24

 

On sait que card(V) = 6.

 

Soit A le nombre de permutations de V.

 

Donc, A = 6 ! = 6 ´ 5 ´ 4 ´ 3 ´ 2 ´ 1 = 720

 

 

 

3-

 

On donne un ensemble fini E de n éléments (n entier naturel non nul).

 

 

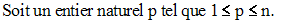
On appelle arrangement p à p des n éléments de E, toute permutation de p quelconques des n éléments de E.

 

Deux arrangements p à p distincts diffèrent soit par l’ordre soit par la nature des éléments qui les constituent.

 

On se propose de calculer le nombre de ces arrangements.

 

On procède comme à l’exercice 2 ci-dessus.

 

On se donne p cases numérotés de 1 à p, dans chacune d’elles on place un élément de E.
Pour chaque case, on a successivement :

 

n, n – 1, n – 2, … , n – (p – 1) = n – p + 1 choix possibles.

 

Le produit de ces p nombres est le nombre total de choix possibles, c’est-à-dire le nombre des
arrangements p à p des n éléments de E.

 

Ainsi le nombre des arrangements p à p des n éléments de E est égal à :

 

n × (n – 1) × (n – 2) × (n – 3) ×….× (n – p + 1) qui sera noté :

 

 

En particulier :

 

 

 

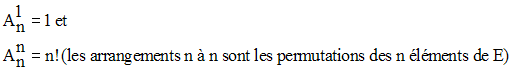
Application

 

Soient deux ensembles finis quelconques E et F, tels que :

 

0 < p = card(E) ≤ card(F) = n

 

 

 

Exercices

On te donne A = {1, 5} et B = {a, e, i}.

 

Calcule le nombre des applications injectives de A dans B.

 

Définis par extension leurs graphes respectifs.

 

Solution

 

Soit N le nombre des applications injectives de A dans B.

 

On a :

 

 

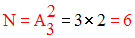
Soient f, g, h, i, j, k ces 6 injections.

 

 

On te donne l’ensemble E = {1, a, 3, d, 5}.

 

Calcule le nombre des arrangements 2 à 2 des 5 éléments de E.

 

Calcule le nombre d’arrangements 3 à 3 des 5 éléments de E.

 

Calcule le nombre d’arrangements 4 à 4 des 5 éléments de E.

 

Calcule le nombre des permutations de E.

 

Solution

 

Le nombre des arrangements, 2 à 2, des 5 éléments de E est :

 

 

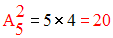
Le nombre des arrangements, 3 à 3, des 5 éléments de E est :

 

 

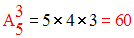
Le nombre des arrangements, 4 à 4, des 5 éléments de E est :

 

 

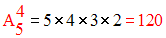
Le nombre de permutations de E est :

 

5! = 5 ´ 4 ´ 3 ´ 2 ´ 1 = 120.

 

 

 

4-

 

On donne un ensemble fini E de n éléments (n entier naturel non nul).

 

 

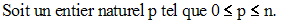
On appelle combinaison p à p des n éléments de E tout sous-ensemble ou partie de E constitué de p éléments.

 

Deux combinaisons p à p distinctes diffèrent par la nature des éléments qui les constituent :
aucune considération d’ordre n’intervient.

 

On se propose de calculer le nombre des combinaisons p à p des n éléments de E.

 

Tout arrangement p à p des n éléments de E peut être considéré comme une permutation des p éléments
d’une combinaison p à p ; Par conséquent, si nous dressons la liste des toutes les permutations des éléments
des diverses combinaisons p à p, nous obtenons tous les arrangements p à p.

 

En outre, deux arrangements de cette liste diffèrent :

soit par la nature de leurs éléments, s’ils ont été obtenus à partir de deux combinaisons distinctes ;

soit par l’ordre de leurs éléments, s’ils ont été obtenus à partir de la même combinaison.

 

Ainsi, chaque combinaison p à p a généré p ! arrangements p à p.

 

 

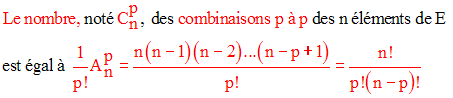
Cas particuliers :

 

 

 

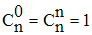
Exercice 

 

On te donne l’ensemble E = {a, b, c, d ,e}

 

 

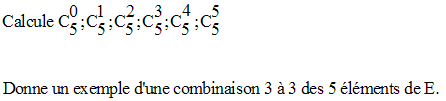
Solution

 

 

{b, c, e} est une combinaison, 3 à 3, des 5 éléments de E.

 

Propriétés

 

Toute combinaison p à p des n éléments de E est une partie constituée de p éléments de E.
La partie complémentaire de cette partie est une combinaison

(n – p) à (n – p) des n éléments de E.

 

Comme le cardinal de P(E) est un entier pair, il y adonc autant de combinaisons p à p que de combinaisons
(n – p) à (n – p) des n éléments de E.

 

 

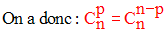
On fixe un élément a quelconque de E.

 

Les combinaisons p à p des n éléments de E peuvent se répartir en deux classes :

L’une formée des combinaisons qui ne contiennent pas l’élément a : ce sont les combinaisons p à p des

(n – 1) éléments autres que a ; l’autre formée des combinaisons qui contiennent a :
on les obtient par adjonction de a à chacune des combinaisons (p – 1) à (p – 1) des (n – 1)
éléments autres que a.

 

Par conséquent, on obtient la relation suivante :

 

 

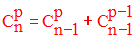
Exercice

 

On donne le tableau suivant :

 

 

 

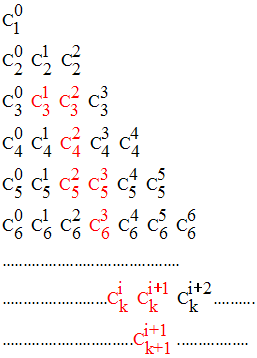
Calcule tous les termes de ce tableau.

 

Que peux-tu affirmer pour les termes en rouges de type :

 

 

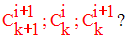
Ce tableau s’appelle triangle de Pascal.

 

Chaque ligne contient tous les coefficients de l’expression :

 

 

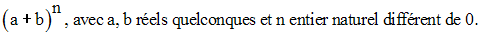
On admettra la formule suivante dite binôme de Newton :

 

 

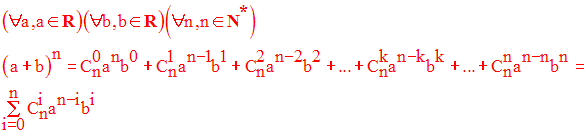
A l’aide de cette formule et du triangle de Pascal, calcule :

 

 

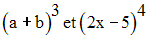
Solution

 

En appliquant la formule donnant le nombre de combinaisons, ainsi que ses propriétés, on trouve successivement :

 

1

 

1  2  1

 

1  3  3  1

 

1  4  6  4  1

 

1  5  10  10  5  1

 

1  6  15  20  15  6  1

 

………….................................

 

 

En appliquant la propriété :

 

 

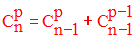
on trouve :

 

 

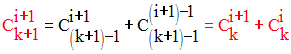
C’est grâce à cette relation que l’on calcule chaque ligne du tableau ; par exemple :

 

La troisième ligne est déduite de la seconde en appliquant la relation ci-dessus ; ainsi on a :

 

1 ; 1 + 2 = 3 ; 2 + 1 = 3 ; 1.

 

La quatrième ligne est déduite de la troisième en appliquant la même relation ; ainsi on a :

 

1 ; 1 + 3 = 4 ; 3 + 3 = 6 ; 3 + 1 = 4 ; 1.

 

Et ainsi de suite….

 

 

La formule de Newton donne :

 

 

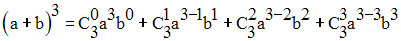
Or, les termes de la troisième ligne du triangle de pascal sont :

1 ; 3 ; 3 ; 1

 

On obtient ainsi :
 

 

 

 

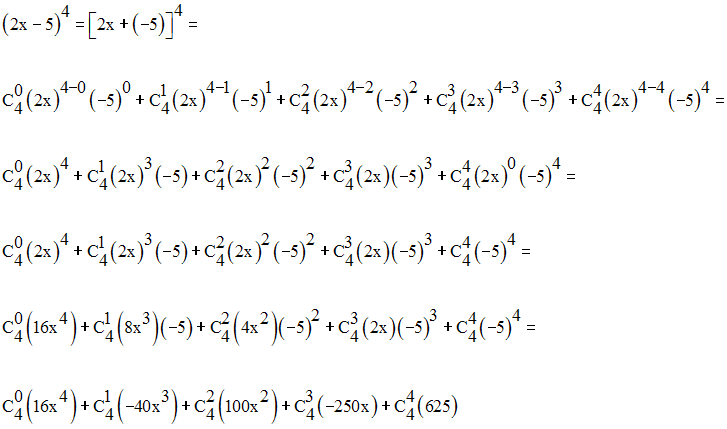
Or, les termes de la quatrième ligne du triangle de pascal sont :

1 ; 4 ; 6 ; 4 ; 1

 

On obtient ainsi :

 

 

 

 

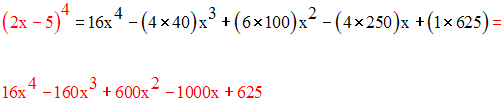
5-

 

A l’aide de la formule de Newton, montre que :

 

 

Solution

 

Soit E un ensemble fini quelconque dont le cardinal est n.

 

On sait qu’une combinaison quelconque, p à p ( p étant inférieur à n), des n éléments de E est un
sous-ensemble de E composé de p éléments.

 

 

 

 

 

 

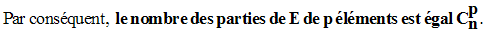
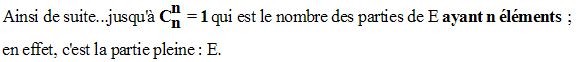
Le nombre total des parties de E est donc égal à :

 

 

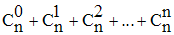
Dans le binôme de Newton, en faisant a = b = 1, on obtient :

 

 

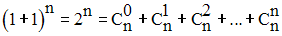
Or, le cardinal de P(E) est le nombre :

 

 

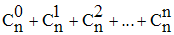
Donc, finalement on obtient :

 

 

 

 

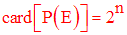
6-

 

On donne la donnée (A, B, f) d’une relation f définie par :

 

 

7-

 

On donne les 10 premiers chiffres dits chiffres arabes :

0, 1, 2, …, 9

Combien de nombres de sept chiffres tous distincts peut-on former avec ces chiffres ?

 

 

 

8-

 

Soient n points distincts appartenant à un cercle.

Combien ces points déterminent-ils de droites ?

Combien existe-t-il de triangles ayant leurs sommets en ces points ?

Combien ces mêmes points déterminent-ils des vecteurs tous différents du vecteur nul ?

 

 

 

9-

 

On considère l’ensemble des 26 lettres de l’alphabet français.

Combien peut-on, avec ces lettres, former de groupes de 6 lettres sans s’intéresser à l’ordre
de ces dernières et tels que :

1)    les groupes ne contiennent aucune voyelle ?

2)    les groupes contiennent une voyelle et une seule ?

3)    les groupes contiennent au moins une voyelle ?

 

 

 

10-

 

Soit E un ensemble fini de cardinal l’entier naturel n.

 

On suppose que n ≥ 2

 

On appelle transposition de E, une permutation de E qui laisse invariants tous les éléments de E sauf deux.

 

Soit t une transposition de E.

 

Par définition, on a :

 

 

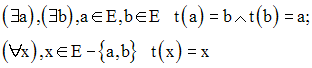
Montre que t est une involution.

 

 

 

11-

 

On donne l’application (Z, N, f) définie par :

 

 

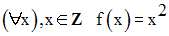
On donne également une application (N, N, g) définie par :

 

 

 

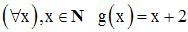
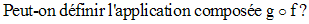
Si oui, explicite sa source, son but et son expression.

 

 

 

 

fin de la deuxième partie

clique ici pour se diriger vers la troisième partie

retour au sommaire