NOTIONS ELEMENTAIRES DE LA
THEORIE DES ENSEMBLES ET DE TOPOLOGIE
1ère partie
1. Définitions et généralités
Il n’est pas
facile de donner une définition à un ensemble. Mais intuitivement, on peut
affirmer qu’un ensemble,
noté généralement par une lettre majuscule, est une collection d’objets
appelés éléments
et notés généralement par
des lettres minuscules.
Soit A un ensemble et x un objet.
Si x est un élément de A, alors on écrira :
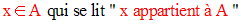
Si y est un objet n’appartenant pas à
A, on écrira :
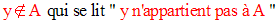
Il existe un
ensemble qui ne contient aucun élément ; il
est appelé ensemble vide et sera noté par
le
symbole :


Un ensemble E est dit fini lorsque le nombre de ses éléments est un entier fini.
Ce nombre sera appelé cardinal de E et sera noté card(E) ou encore n(E).
Par définition on a :
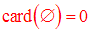
Exemple : l’ensemble V des voyelles de l’alphabet français est fini et on a :
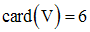
Un ensemble est dit infini lorsqu’il contient une infinité d’éléments.
Exemple : l’ensemble des entiers naturels.
On définit un ensemble de deux manières différentes :
Par extension, en établissant la liste de ses éléments entre deux accolades
Exemple : {a, e, i, o, u, y}
Par compréhension, en déclarant une propriété vérifiée par tous ses éléments
Exemple :{x ; x entier naturel}
Généralement, les ensembles infinis sont définis par compréhension.
Tout ensemble contenant un et un seul élément est appelé singleton.
Exemple : F = {a}
Tout ensemble contenant deux et seulement deux éléments est appelé paire.
Exemple : G = {1, i}
2. Inclusion
et égalité des ensembles
Soient deux ensembles quelconques A, B.
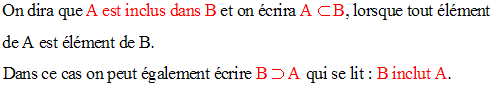
Souvent on dit que A est un sous ensemble de B ou encore que A est une partie de B.
On a la tautologie suivante :
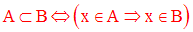
Exemples :
Si P est l’alphabet français, alors on a :
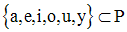
Si A est l’ensemble des chiffres, alors, en notant, N, l’ensemble des entiers naturels, on a :
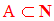
Exercice
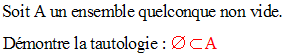
Solution

On dira que
l’ensemble A est égal à l’ensemble B, ou
encore A et B sont égaux, si et seulement
si
on a :
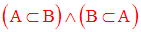
Dans ce cas on écrira A = B.
Cela signifie que tout élément de A appartient à B et que tout élément de B appartient à A.
On a la tautologie suivante :
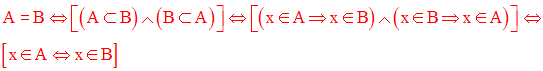
On a la tautologie suivante :
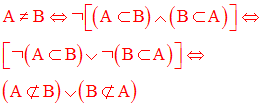
Intuitivement,
deux ensembles A, B sont distincts, lorsque l’un d’eux contient au
moins un élément
n’appartenant pas à l’autre.
Remarque
Si A, B sont finis et A = B alors card(A) = card(B) ; mais la réciproque est fausse.
3.
Intersection des ensembles
Soient deux ensembles quelconques A, B.
L’intersection de A, B est un ensemble dont les éléments appartiennent simultanément à A et à B.
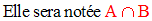
On a la tautologie suivante :
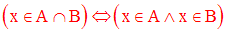
Exemple :
A = {a, i, b, p} ; B = {2, a, 3, q, i}.
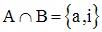
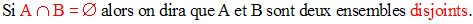
Ainsi l’ensemble des entiers pairs et celui des entiers impairs sont deux ensembles disjoints.
L’intersection des ensembles est commutative.
A, B étant deux ensembles quelconques, alors on a :
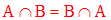
En effet, on a :
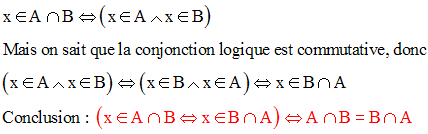
L’intersection des ensembles est associative.
A, B et C étant trois ensembles quelconques, alors on a :
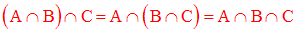
A titre d’exercice, démontre-la en utilisant l’associativité de la conjonction logique.
Exercice
Montre les tautologies suivantes :
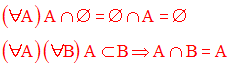
Solution
Soient A, B deux ensembles quelconques.

On sait que l’équivalence logique est transitive ; donc :
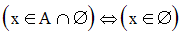
Cette dernière équivalence logique s’écrit aussi :

De plus, l’intersection des ensembles étant commutative, on a :

Par ailleurs,
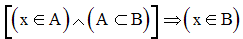
Ainsi, tout élément x de A est élément de B.
x élément commun à A et B, appartient donc à leur intersection et on a :
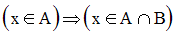
Cette dernière assertion est logiquement équivalente à :
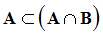
Par conséquent, on obtient :
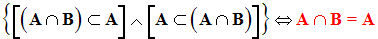
Conclusion :
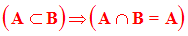
4. Réunion des ensembles
Soient deux ensembles quelconques A, B.
La réunion de A, B est un ensemble dont les éléments appartiennent à A ou à B ou à leur intersection.
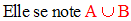
On a la tautologie suivante :
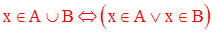
Exemple :
A = {a, i, b, p} ; B = {2, a, 3, q, i}.
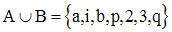
Exercice
Montre les tautologies suivantes:
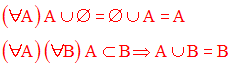
La réunion des ensembles est commutative.
A, B étant deux ensembles quelconques, alors on a :

En effet, on a :
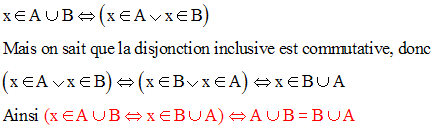
Exercice
Monter que la réunion des ensembles est associative.
C’est-à-dire que :
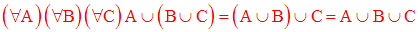
Remarque : tu
utiliseras l’associativité de la disjonction inclusive.
5. Distributivité de l’intersection et de la réunion, l’une par rapport à l’autre.
L’intersection des ensembles est distributive à gauche par rapport à la réunion des ensembles :
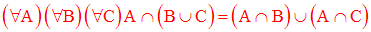
En effet on a :

L’intersection des ensembles est distributive à droite par rapport à la réunion des ensembles :
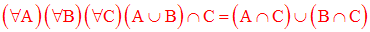
De la même manière que ci-dessus, et en utilisant
la distributivité à droite de la conjonction logique
par rapport
à la disjonction inclusive, montre la distributivité à droite, de
l’intersection des ensembles
par rapport à la réunion
des ensembles.
L’intersection des ensembles étant
simultanément distributive à gauche et distributive à droite
par
rapport
à la réunion des ensembles, on dira que
l’intersection des ensembles est distributive
par rapport à la
réunion
des ensembles.
La réunion des ensembles est distributive à gauche par rapport à l’intersection des ensembles :
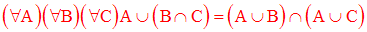
Exercice
Montre cette
propriété en utilisant la distributivité à gauche, de la disjonction
inclusive par
rapport à la conjonction logique.
La réunion des ensembles est distributive à droite par rapport à l’intersection des ensembles :
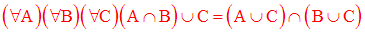
Exercice
Montre cette
propriété en utilisant la distributivité à droite, de la disjonction
inclusive par rapport
à la conjonction logique.
La réunion des ensembles étant simultanément
distributive à gauche et distributive à droite par
rapport à
l’intersection
des ensembles, on dira que la réunion des
ensembles est distributive
par rapport à l’intersection des
ensembles.
Vérifications par l’exemple
On donne :
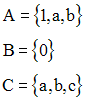
On a :
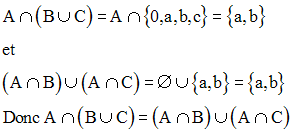
Montre que l’on a également :
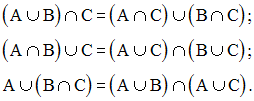
6. Cardinal de la réunion de deux ensembles finis quelconques
On donne deux ensembles finis quelconques A, B.
Soient a = card(A) et b = card(B).
On admettra la relation suivante :
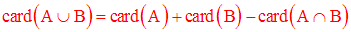
Dans le cas particulier où A et B sont disjoints, cette relation devient :
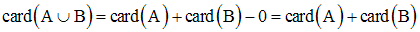
Exercice
On te donne trois ensembles finis E, F et G.
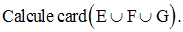
Solution
La réunion des ensembles étant associative, on a :
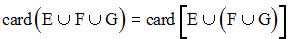
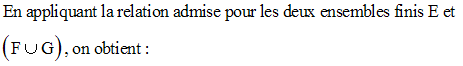
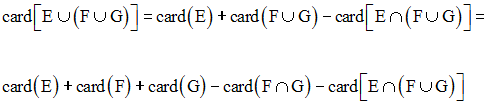
L’intersection des ensembles étant distributive par rapport à la réunion des ensembles, on a :
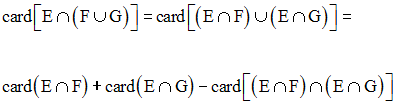
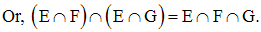
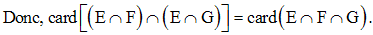
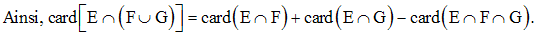
Finalement, on obtient :
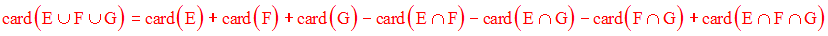
7. Partition d’un ensemble
On donne un ensemble quelconque E.
On appelle ensemble des parties de E, l’ensemble de toutes les parties de E.

Ainsi, par définition on a :
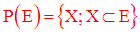
Toute partie de E différente de la partie pleine et de la partie vide est appelée partie propre.
Exemples
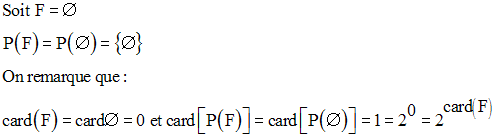
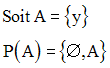
On remarque que :
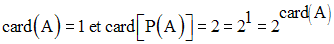
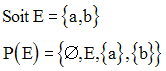
On remarque que :
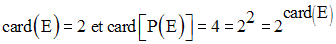
On démontrera par
la suite (analyse combinatoire) que
pour tout ensemble fini E de cardinal n,
l’ensemble P(E) des ses parties
est fini et son cardinal vaut :
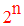
Exercice
Définis par extension les ensembles suivants :
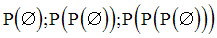
Solution
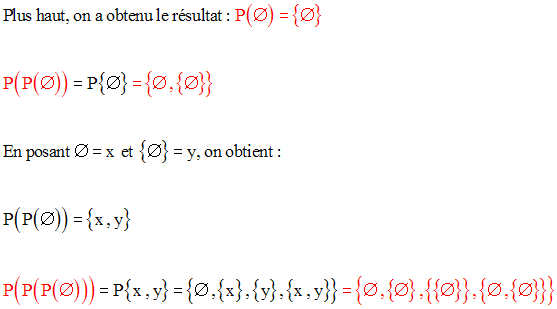
Partition d’un ensemble
On donne un ensemble quelconque E. P(E) est l’ensemble de ses parties.
Un ensemble A est
une partition de E si et seulement si
les conditions suivantes
sont simultanément vérifiées :

Remarque : La troisième condition exprime que deux éléments distincts de A sont disjoints.
Exemples
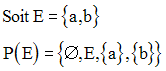
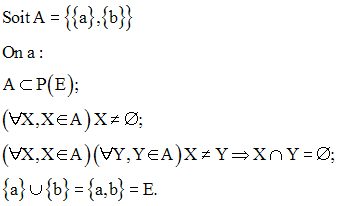
Donc A est une partition de E.
Exercice
Soit B = {E, {a}}.
Montre que B n’est pas une partition de E.

Soit N l’ensemble des entiers naturels.
On pose P l’ensemble des entiers naturels pairs et I celui des entiers naturels impairs.
Soit E = {P, I}
E est-il une partition de N ?
8. Partie complémentaire d’une partie d’un ensemble
Soit E un ensemble quelconque.
Soit A une partie quelconque de E.
La partie complémentaire de A dans E est l’ensemble de tous les éléments de E n’appartenant pas à A.
Elle est notée indifféremment :
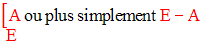
On a la tautologie suivante :
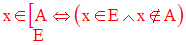
9. Parties complémentaires de l’intersection et de la réunion de parties d’un ensemble
Soit E un ensemble quelconque.
Soient deux parties quelconques A, B de E.
On a les deux propriétés suivantes :
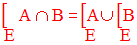
On dira que
la partie complémentaire de l’intersection est la
réunion des parties complémentaires et
que la partie complémentaire de la réunion est l’intersection des parties
complémentaires.
On va montrer la première propriété.

Exercice
Montre, de la même manière la seconde propriété.
Exemple
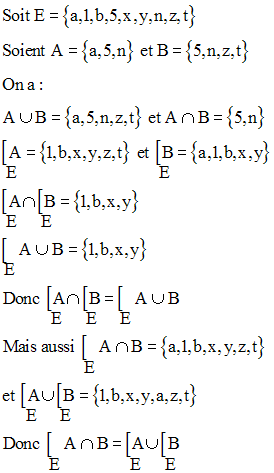
10. Différence dissymétrique
Soient E, F deux ensembles quelconques.
L’ensemble des éléments de E n’appartenant pas à F est par définition la différence notée :
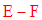
On a donc la tautologie suivante :
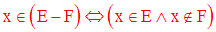
L’ensemble des éléments de F n’appartenant pas à E est par définition la différence notée :
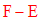
On a donc la tautologie suivante :
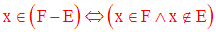
Exercice
La différence dissymétrique est-elle commutative : c’est-à-dire E – F est-il égal à F – E ?
Exemple
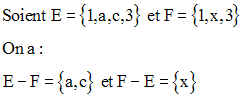
Cas particulier
Si F est une partie de E, alors :
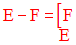
11. Différence symétrique
Soient E, F deux ensembles quelconques.
La réunion des deux ensembles E – F et F – E est appelée différence symétrique et est notée :
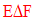
On a la tautologie suivante :
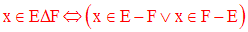
Exercice
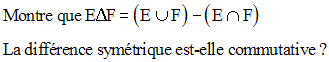
12. Des ensembles particuliers
On a vu que l’ensemble des entiers naturels est noté N.
N privé de son élément 0 est noté :
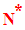
Ainsi on a :
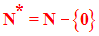
L’ensemble des entiers relatifs, tels que – 4, – 13, + 12, est noté :

Z privé de son élément 0 est noté :
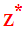
Ainsi on a :
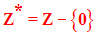
L’ensemble des entiers largement positifs (resp. strictement positifs) est noté :
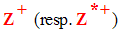
L’ensemble des entiers largement négatifs (resp. strictement négatifs) est noté :
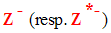
Un nombre a est
dit rationnel si et seulement s’il
existe deux entiers relatifs p et q,
avec q non nul, tels que :
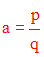
Sinon, il sera appelé nombre irrationnel.
Exemples
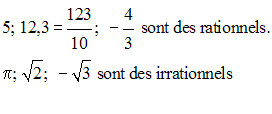
L’ensemble des nombres rationnels est noté Q.
Exercice
Explicite les ensembles suivants :

La réunion de Q et de l’ensemble des nombres irrationnels est appelé ensemble des nombres réels.
Il est noté R.
Exercice
Explicite les ensembles suivants :
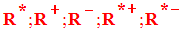
Un nombre a est dit nombre complexe ou imaginaire lorsqu’il peut se mettre sous la forme :
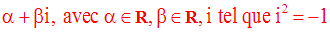
Exemple :
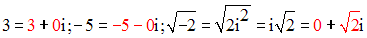
L’ensemble des nombres complexes est noté C.
Exercice
Explicite l’ensemble C*.
Propriété
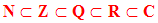
fin de la première partie