
NOTIONS ELEMENTAIRES DE LOGIQUE FORMELLE
1.Généralités et définitions
On appelle proposition ou assertion tout énoncé dont la véracité ou la fausseté est définie.
Ainsi, pour cet énoncé, on pourra répondre sans ambiguïté à la question « est-il vrai ou faux ? ».
Exemples
L’énoncé « La Terre tourne autour du Soleil » est un énoncé vrai ; donc cet énoncé est une assertion.
L’énoncé p défini par « pour tout réel x, x2 + x + 1 > 0 » est vrai ; donc p est une assertion ou proposition.
L’énoncé q défini par « tout rectangle est un carré » est faux ; donc q est une proposition ou assertion.
L’énoncé r défini par « y + 2 < 0 » a sa véracité (ou sa fausseté) qui dépend de la valeur donnée à y.
Si y est strictement inférieur à – 2 alors r est vrai, sinon r est faux.
Ainsi, la véracité (ou la fausseté) de r n’est pas définie ; r n’est pas une assertion.
Soit p une assertion quelconque.
Deux cas possibles peuvent se présenter :
p vraie,
p fausse.
La valeur de vérité de p, notée v(p), est un entier qui est égal à 1 si p est vraie, à 0 si p est fausse.
On peut facilement montrer que pour toute assertion p, l’assertion suivante est vraie :

Soit maintenant une seconde assertion quelconque q. Pour p, q données simultanément,
quatre cas possibles peuvent se présenter :
p vraie, q vraie ;
p vraie, q fausse ;
p fausse, q vraie ;
p fausse, q fausse.
On généralisera sans le démontrer que pour n (n entier naturel non nul) assertions données simultanément
p1, p2, …, pn (n entier naturel différent de 0 et fini), le nombre de cas possibles pouvant
se produire est égal à 2n.
Considérons l’assertion « pour tout réel x, x2 + x + 1 > 0 ».
On peut également énoncer « quel que soit le réel x, x2 + x + 1 > 0 ».
Le groupe de mots « pour tout(te) » ou encore « quel(le) que soit » seront notés par le symbole
suivant appelé quantificateur universel :

Ainsi l’assertion s’écrit :

Considérons l’assertion « il existe au moins un réel x tel que x + 3 < 0 ».
Le groupe de mots « il existe un(e) » sera noté par le symbole suivant appelé quantificateur existentiel :

Ainsi cette assertion s’écrit :

Le symbole noté :

se lit « il existe au moins un(e) et un(e) seul(e) »
Exemple :

Remarque importante :
Les quantificateurs sont des objets mathématiques à part entière ; ils ne doivent pas être utilisés
comme abréviation (sténographie) dans la rédaction d’une phrase ou d’un texte.
Ainsi les écritures suivantes sont interdites :

2. Equivalence logique
Soient deux assertions quelconques p, q.
On dira que p, q sont logiquement équivalentes si et seulement si elles ont la même valeur de vérité,
c’est-à-dire si elles sont simultanément vraies ou simultanément fausses.
Dans ce cas on écrira :
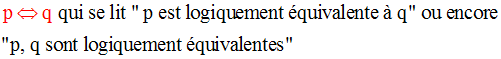
Ainsi, pour toutes assertions p, q, l’assertion suivante est vraie :

3. Négation d’une assertion
Soit p une assertion quelconque.
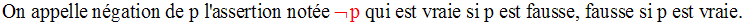
En effet, pour p il y a deux cas possibles v(p) = 1, v(p) = 0.

4. Conjonction logique
Soient deux assertions quelconques p, q.

Nommons A cette conjonction logique.
Le tableau suivant appelé
table de vérité met en
évidence cette définition :
|
p |
q | A |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
En s’appuyant sur ce tableau on peut montrer que quelles que soient les assertions p, q, l’assertion :

est vraie.
On peut également montrer que l’assertion :

Exercice
On te donne trois assertions quelconques p, q, r.
Démontre en utilisant le résultat :

trouvé ci-dessus, que l’assertion suivante :

On dira que la conjonction logique est associative.
5. Disjonction inclusive
Soient deux assertions quelconques p, q.

Nommons B cette disjonction inclusive.
La table de vérité suivante met en évidence cette
définition :
| p | q | B |
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
Exercice
Démontre que l’assertion suivante est vraie pour toutes assertions p, q :

Montre la commutativité et l’associativité de la disjonction logique.
6.Disjonction exclusive
Soient deux assertions quelconques p, q.

Nommons C cette disjonction exclusive.
La table de vérité suivante met en évidence cette
définition :
| p | q | C |
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Exercice
Montre que l’assertion suivante est vraie pour toutes assertions p, q :

En déduire la valeur de v(pWq) en fonction de v(p) et v(q).
Montre que la disjonction exclusive est commutative. Est-elle associative ?
7. Implication logique
Soient deux assertions quelconques p, q.

Nommons D cette implication logique.
La table de vérité suivante met en évidence cette
définition :
| p | q | D |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Exercice
L’implication logique est-elle commutative ?
A l’aide d’une table de vérité, montre que pour toutes assertions p, q, l’assertion suivante est vraie :

Montre que l’assertion suivante est vraie :

On dira que l’implication logique est réflexive.
On te donne une troisième assertion r. Montre que pour toutes p, q, r, l’assertion suivante est vraie :

On dira que l’implication logique est transitive.
Montre également que l’assertion suivante est vraie :

On dira que l’implication logique est antisymétrique.
Au second paragraphe on a donné la définition de l’équivalence logique.
Montre qu’elle est réflexive ; c’est-à-dire que pour toute assertion p, l’assertion :

Montre que pour toutes assertions p, q, l’assertion suivante est vraie :

On dira que l’équivalence logique est symétrique.
Est-elle antisymétrique ?
Montre qu’elle est transitive ; c’est-à-dire que pour toutes assertions p, q, r, l’assertion :

8. Distributivité de la conjonction logique et de la disjonction inclusive, l’une par rapport à l’autre
On donne trois assertions quelconques p, q, r.
On montre que l’assertion suivante est vraie :

On a successivement :

Ainsi, on a :

On dira que la conjonction logique est distributive à gauche par rapport à la disjonction inclusive.
On montrera de la même manière qu’elle est distributive à droite par rapport à la disjonction inclusive, c’est-à-dire :

Exercice
Montre de la même manière que la disjonction inclusive est distributive par rapport à la conjonction logique.
9. Lois de Morgan
On donne deux assertions quelconques p, q.
On a :

Exercice
Montre que la négation d’une
disjonction inclusive est logiquement équivalente à la conjonction
logique des négations ;
c’est-à-dire que pour toutes assertions p, q,
l’assertion suivante est vraie :

Ce sont là les deux lois de Morgan .
10. Tautologie
Les symboles :

Soit une assertion A composée d’une suite
finie d’assertions élémentaires
quelconques ei
et de connecteurs logiques.
On dira que A est une tautologie
si et seulement si elle est vraie quelles que soient les valeurs de vérité
affectées aux assertions élémentaires ei.
On a précédemment rencontré plusieurs tautologies telles que :

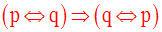

Exercice
a- Montre la tautologie :

b- Montre la tautologie :

C’est sur cette tautologie qu’est basée la démonstration par l’absurde.

c- Montre la tautologie :

C’est sur cette tautologie qu’est basée la démonstration par la contraposée.
d- Montre l’identité :

Que peux-tu en déduire ?
Que peux-tu affirmer pour l’assertion :
