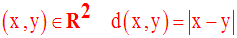
m étant un réel fini ou infini, comment démontrer qu'une fonction numérique admet m comme limite, lorsque x tend vers a (a réel fini ou infini) ?
Dans tout ce qui suit, on supposera E = F = R et R muni de la distance d définie par :
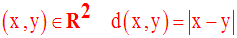
L’ensemble des intervalles ouverts de R qui découle de ces hypothèses est
une topologie
de R associée à d.
Dans ces conditions, f est dite fonction numérique ou fonction réelle d’une variable réelle.
1- Rappel
Soient I un intervalle de R et f une fonction numérique de I dans R.
Soit a un élément réel fini tel que :
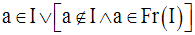
Soit A la partie de R définie comme suit :
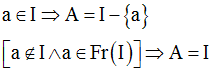
Tout voisinage Va de a rencontre A ; donc a est adhérent à A et on a :
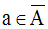
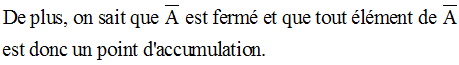

On dira que f(x) a une
limite k quand x appartenant à A tend vers a si,
pour tout voisinage
Vk de k dans R, il existe au moins un voisinage Va de
a dans R tel que :
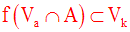
On note donc :
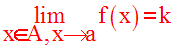
Cette écriture est logiquement équivalente à la suivante :
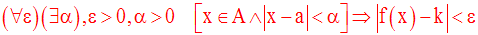
C’est cette écriture
qu’il faudra utiliser pour démontrer qu’une fonction numérique
tend vers une limite k, réel fini donné, lorsque x tend vers a.
2- Extension de la notion de limite
Soit A un réel strictement positif quelconque.


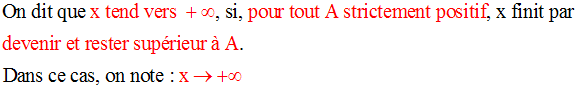


Cette définition est logiquement équivalente à la suivante :
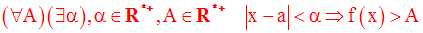

Cette définition est logiquement équivalente à la suivante :
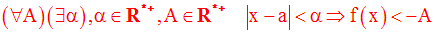
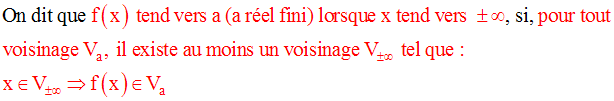
Cette définition est logiquement équivalente à la suivante :
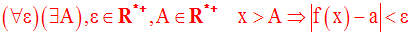
ou
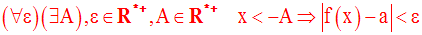
On pourra définir de la même manière l’expression suivante :
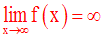
en prêtant attention aux différents signes que peut prendre l’infini.
f étant une fonction numérique, on dira qu’elle
est définie à droite de a (a réel fini), s’il
existe
au moins un réel h strictement positif tel que f soit définie dans l’intervalle
]a , a + h[.
On dira qu’elle est définie à gauche de a (a réel
fini), s’il existe au moins un réel k
strictement positif tel que f soit définie dans l’intervalle ]a – k , a[.
Soit f une fonction numérique définie à droite de a (a réel fini).
On dit que f(x) tend
vers l (l réel fini) lorsque x tend vers a à droite, si et seulement si,
quel
que soit l’intervalle J de centre l, il existe au moins un intervalle I, de la
forme ]a , a + h[
(h réel fini strictement positif), et tel que f(I) est inclus dans J.
Dans ce cas on écrira :
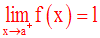
Souvent l’expression : « x tend vers a à
droite » est équivalente à l’expression :
« x tend vers a positivement ou
par valeurs supérieures ».
Avec les quantificateurs, la définition de la limite de f à droite au point a s’écrit :
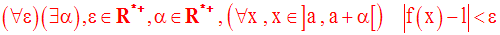
ou
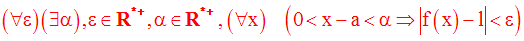
Soit f une fonction numérique définie à gauche de a (a réel fini).
On dit que f(x) tend
vers m (m réel fini) lorsque x tend vers a à gauche, si et seulement si,
quel que soit l’intervalle K de centre m, il existe au moins un intervalle L, de
la forme
]a – h , a[ (h réel fini strictement positif), et tel que f(L) est inclus dans
K.
Dans ce cas on écrira :
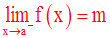
Souvent l’expression : « x tend vers a à
gauche » est équivalente à l’expression :
« x tend vers a négativement ou
par valeurs inférieures ».
Avec les quantificateurs, la définition de la limite de f à gauche au point a s’écrit :
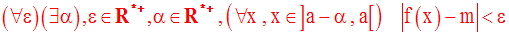
ou
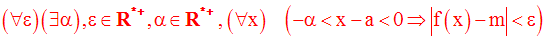
Remarques
A -
On démontre facilement que si les limites, à droite et à gauche, existent, alors elles sont uniques.
B -
Pour qu’une fonction
numérique admette une limite en un point il faut et il suffit que ses
limites à droite et à gauche en ce point soient égales.
C -
Dans des ouvrages, la limite de f à droite au point a, si elle existe, est souvent notée :
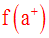
La limite de f à gauche au point a, si elle existe, est souvent notée :
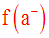
Ainsi, on a :
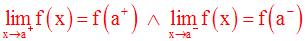
Il ne faut pas confondre les notations :
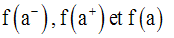
qui peuvent avoir des valeurs différentes.
On a donc l’équivalence logique suivante :

3- Limite et continuité d’une fonction numérique en un point
On a l’équivalence logique suivante :
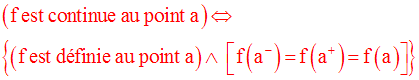
4- Applications
Application 1
Soit la fonction numérique f définie comme suit :
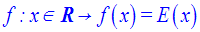
On rappelle que f est la fonction partie entière.
Soit n un entier relatif quelconque.
f admet-elle une limite à droite ? une limite à gauche ?
f admet-elle une limite au point n ?
Solution
On note d’abord que :
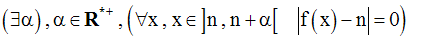
Par conséquent,
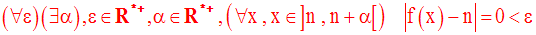
f admet donc une limite à droite au point n et on a :
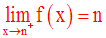
Par ailleurs,
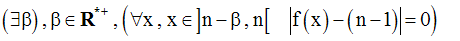
Par conséquent,
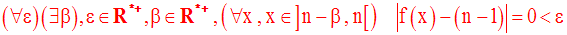
f admet donc une limite à gauche au point n et on a :
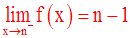
Conclusion :
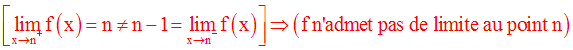
De plus, f n’est pas continue au point n, malgré sa continuité à droite en ce point.
Application 2
Soit la fonction numérique f définie comme suit :
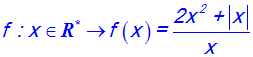
Démontre que l’on a :
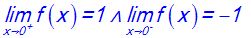
Solution
D’abord on a :
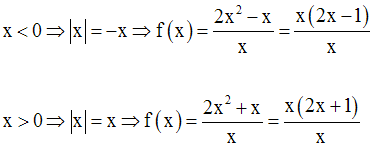
Or, x étant différent de 0, on obtient en simplifiant par x :
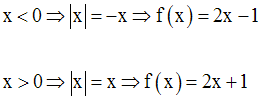
On démontre que l’on a :
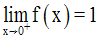
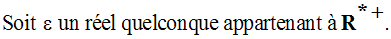
On cherche donc à avoir :
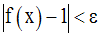
Comme x est strictement positif, on a :
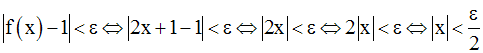
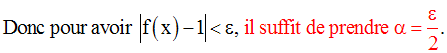
On obtient ainsi :

Par conséquent, on a :
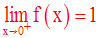
On démontre que l’on a :
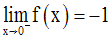
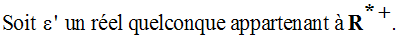
On cherche donc à avoir :
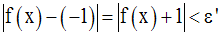
Comme x est strictement négatif, on a :
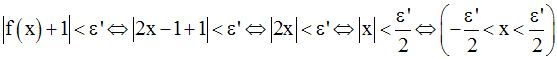
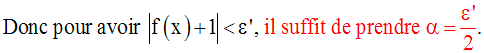
On obtient ainsi :
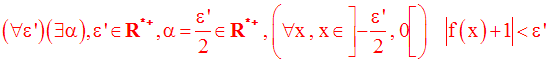
Par conséquent, on a :
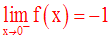
Remarque
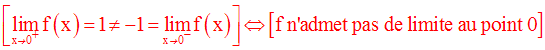
De plus, f est discontinue en ce point.
Application 3
Soit la fonction numérique g définie comme suit :
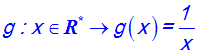
Démontre que l’on a :
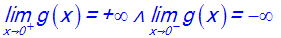
Solution
On démontre que :
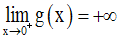
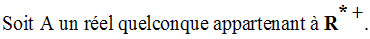
On cherche donc à avoir :
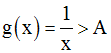
Comme x tend vers 0 positivement, x est strictement positif et l’on a :
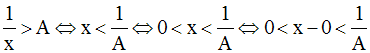
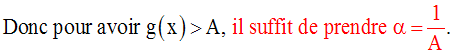
On obtient ainsi :
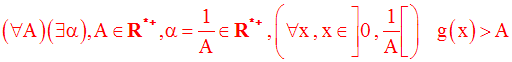
Par conséquent, on a :
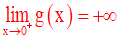
A titre d’exercice, je te laisse démontrer que l’on a :
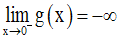
Application 4
Soit la fonction numérique h définie comme suit :
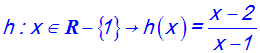
Démontre que l’on a :
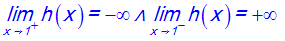
Solution
On démontre que :
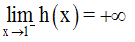
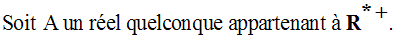
On cherche donc à avoir :
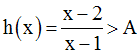
La division de (x – 2) par (x – 1) donne :
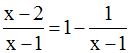
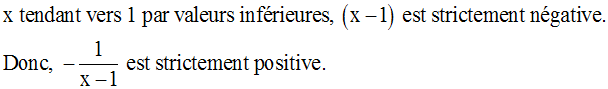
Ainsi,
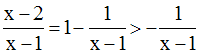
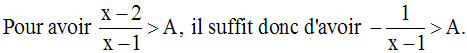
Ainsi, on a :
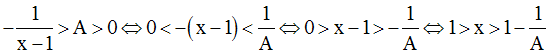
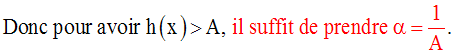
Ainsi, on a :
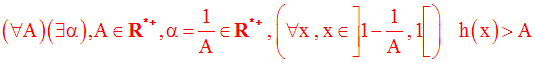
Par conséquent, on a :
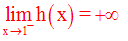
A titre d’exercice je te laisse démontrer que l’on a :
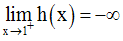
Application 5
Soit la fonction numérique i définie comme suit :
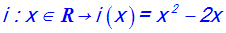
Démontre que l’on a :

Solution
On démontre que :
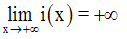
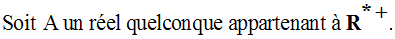
On cherche donc à avoir :
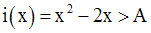
On a :
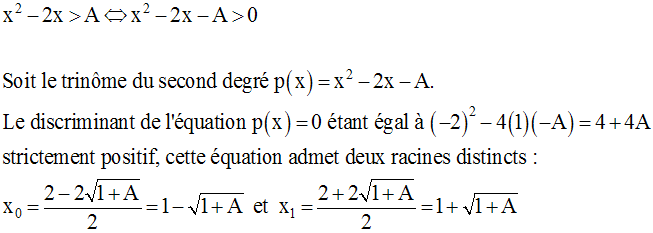
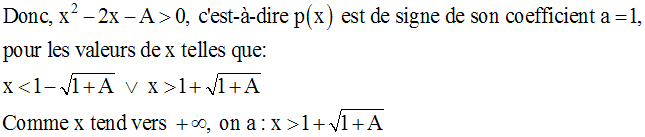

On obtient ainsi :
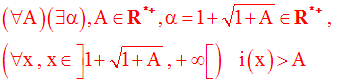
Cette écriture est logiquement équivalente à :
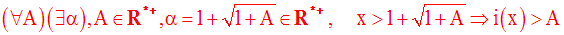
Par conséquent, on a :
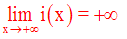
A titre d’exercice je te laisse démontrer que l’on a :
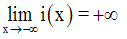
5- Conclusion
Pour démontrer qu’une fonction numérique admet
une limite l donnée lorsque x tend
vers a (a réel fini ou infini), on utilise la définition de la limite d’une
fonction numérique.
Il ne faut pas confondre cette question avec
celle qui consiste à trouver la
limite de la fonction numérique.
Dans le premier cas, la limite est
une donnée du problème ; il s’agit de
démontrer que l’on a :
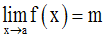
Dans le second cas, la limite est
inconnue et il s’agit de la trouver en
utilisant les propriétés des opérations sur les limites.