
LES FONCTIONS
LOGARITHME NEPERIEN ET EXPONENTIELLE
DE BASE e
I- Fonction logarithme népérien
I-a Définition

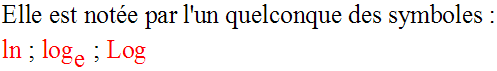

Ainsi on a :
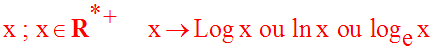
Pour la suite, on utilisera le
symbole Log (avec L majuscule) pour désigner
cette fonction
numérique.
La définition précédente se traduit également par :
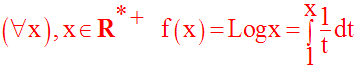

Remarque importante :
La fonction logarithme népérien n’est pas définie pour les réels largement négatifs.
Une écriture telle que Log (-5) n’a pas de sens en mathématiques.
Interprétation géométrique
Interprétons géométriquement la notion de logarithme népérien.
Pour cela, soit un repère
orthonormal et soit la branche hyperbolique (H) de la fonction
numérique définie par :
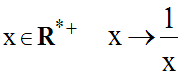
Nous avons représenté graphiquement cette fonction pour les réels x strictement positifs.
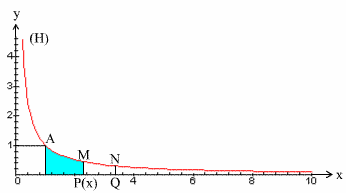
L’aire S, de la surface plane
limitée par l’axe (Ox), la courbe (H), la droite d’équation
x = 1 et la droite d’équation x = a , a quelconque appartenant à R* +
(partie coloriée en bleu) est :
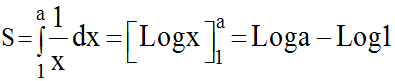
Or on sait que Log 1 = 0 ; donc :
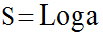
Ainsi, pour tout réel a appartenant au domaine de définition R* +, Loga est une aire.
On peut donc généraliser en annonçant que :
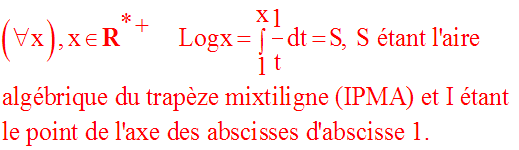
Si x est strictement supérieure à 1, cette aire est strictement positive :
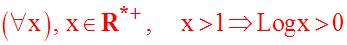
Si x est strictement comprise entre 0 et 1, l’aire est strictement négative :
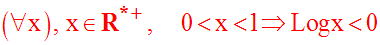
I-b Propriétés
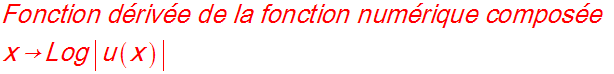
Soit u une fonction numérique,
définie, continue, dérivable et strictement positive
sur un intervalle réel I.

La fonction u étant dérivable sur I, on a :
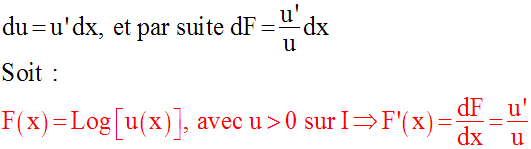
Supposons maintenant que u est
une fonction numérique définie, continue,
dérivable et strictement négative sur un
intervalle réel I.
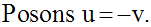
D’après ce qui précède, la fonction composée, G, telle que :
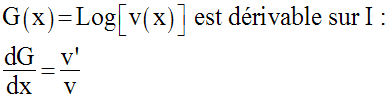
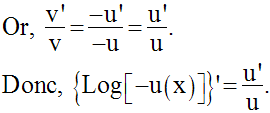
Par conséquent, si u est une
fonction définie, continue, dérivable et de signe
constant sur
un intervalle réel I, alors la fonction, H, telle que :
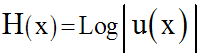
est dérivable sur I et sa dérivée est égale à :
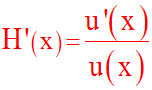
Remarque importante

Exemples
1)
Soit à calculer la dérivée de la fonction numérique f définie par :
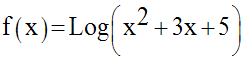
Solution
Le trinôme du second degré en x :
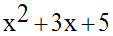
a son discriminant égal à :
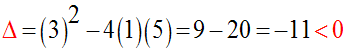
Par conséquent, ce trinôme est de signe de son coefficient a égal à 1 pour tout réel x :
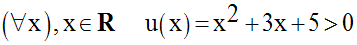
On a donc :
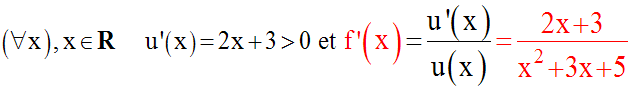
2)
Soit à calculer la dérivée de la fonction numérique g définie par :
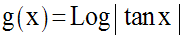
Solution
Trouvons d’abord le domaine de définition de g.
La fonction g n’est pas définie pour :
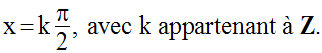
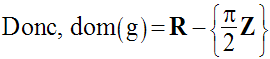
Pour tout réel x appartenant à dom(g), posons :
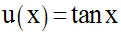
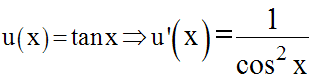
D’où :
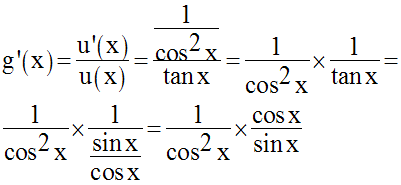
Comme x appartient à dom(g), cos
x est différent de zéro et on peut simplifier par cos x ;
on obtient finalement :
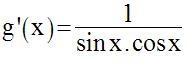
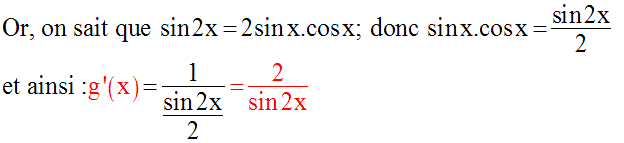
3)
Montrons que les primitives de la fonction numérique g définie par :
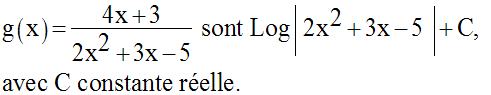
Solution
Déterminons d’abord le domaine de définition de g.
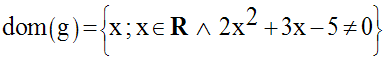
Calculons alors les racines de l’équation :
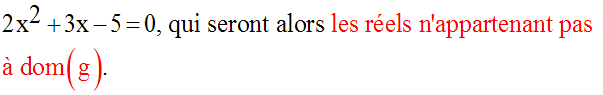

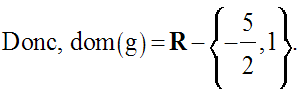
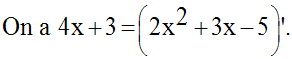
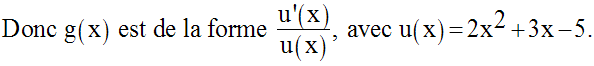
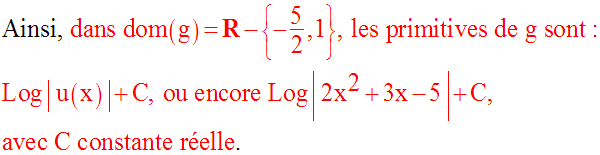
Exercice
Dans un repère orthonormal, on considère la fonction numérique f définie par :
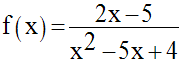
Détermine le domaine de définition E de f.
Etudie f et dresse son tableau de variation. Trace sa courbe représentative (C).
Calcule l’aire du domaine D
limité par la courbe (C), les droites d’équations respectives
x = 1 et x = 4 et l’axe des abscisses.

Soit a un réel strictement positif.
Les fonctions numériques telles que :
sont dérivables sur l’intervalle ] 0 , + ∞ [.
On a donc :
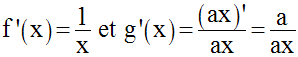
Comme a est différent de zéro, on peut simplifier par a ; on obtient :
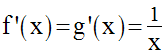
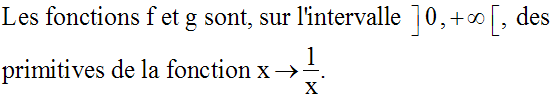
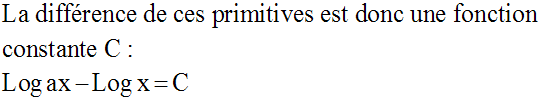
Déterminons C en donnant à x la valeur 1.
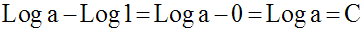
D’où :
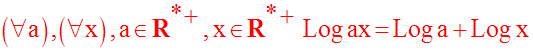
Remarque
Si l’on sait que le produit des réels a et b est strictement positif, on pourra écrire :
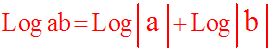
Par récurrence, on en déduit :
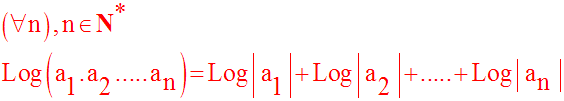
et en posant ai = a, [a > 0 ou (a < 0 avec n pair)], pour tout i élément de {1, 2, …, n}:
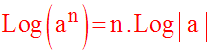
Sous forme condensée :
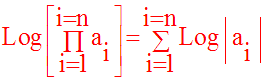
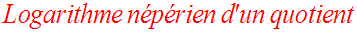
Soient deux réels strictement positifs quelconques a et b.
Il existe au moins un réel strictement positif r et un seul tel que :
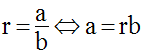
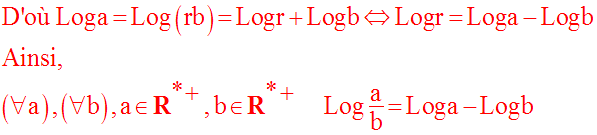

On peut facilement démontrer la relation :
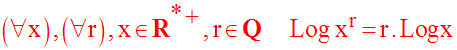
Application :
Soit x un réel quelconque
strictement positif, p un entier relatif
quelconque et q un entier
naturel non nul quelconque ; on a :
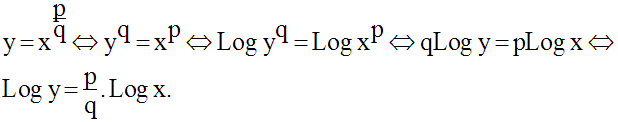
Donc :
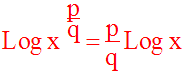
I-c Dérivée logarithmique
Définition
Soit u une fonction numérique,
dérivable sur un intervalle réel I et ne s’annulant pas
sur cet intervalle.
On nomme dérivée logarithmique de u, sur I, le rapport :
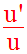
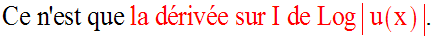
Dérivée logarithmique d’un produit
Soient u et v deux fonctions numériques, dérivables et ne s’annulant pas sur un intervalle réel I.
Le produit :
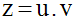
est dérivable et ne s’annule pas sur I.

La propriété s’étend aisément et par récurrence à un produit quelconque de n facteurs, n > 2.
La dérivée
logarithmique d’un produit de facteurs est la somme des dérivées logarithmiques
des facteurs.
Dérivée logarithmique d’un quotient
Soient u et v deux fonctions numériques, dérivables et ne s’annulant pas sur un intervalle réel I.
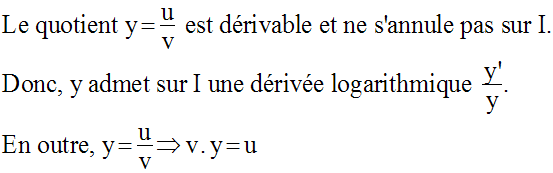
Il s’ensuit que :
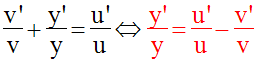
La dérivée
logarithmique d’un quotient est la différence des dérivées logarithmiques
de ses deux termes.
Dérivée logarithmique d'une puissance

I-d Limites
Limite de la fonction logarithme népérien lorsque x tend vers + ∞
L’étude du signe de la dérivée
sur [1 , + ∞[ a montré que la fonction logarithme népérien
est croissante sur cet intervalle.
Supposons qu’elle soit majorée sur cet intervalle.
Elle admettrait donc, lorsque x tend vers + ∞, une limite réelle unique, finie, i, telle que :
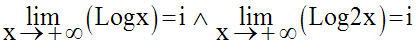
Or, on sait que :
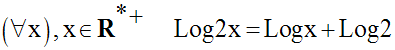
Il s’ensuivrait donc l’égalité des réels :
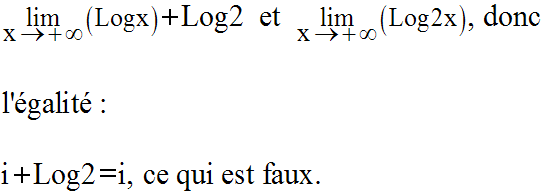
Conclusion :
La fonction logarithme népérien, croissante sur [1 , + ∞[, ne peut être majorée sur cet intervalle.
Donc, lorsque x tend vers + ∞, la fonction logarithme népérien tend également vers + ∞.
On écrit :
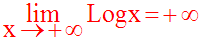
Limite de la fonction logarithme népérien lorsque x tend vers
0 + (x tend vers zéro par
valeurs supérieures)
Soit x un réel strictement positif quelconque et soit son inverse X.
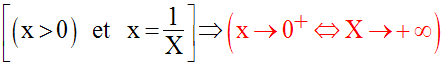
On a :
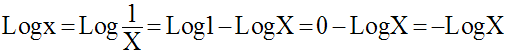
On sait que :
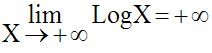
Donc :
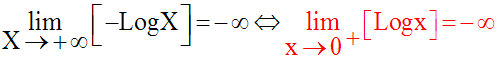
Limites de deux fonctions numériques particulières
Calculons la limite de la fonction numérique f définie par :
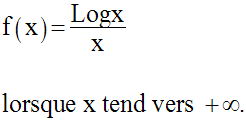
Lorsque x tend vers + ∞, l’expression de f se présente sous la forme indéterminée :
Levons cette indétermination.

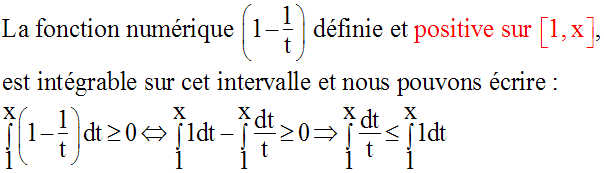
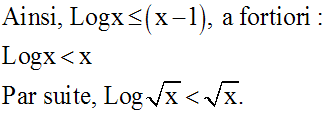
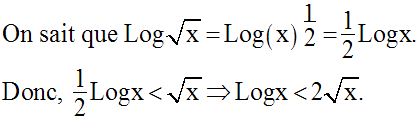
Il s’ensuit que, pour x >1 :
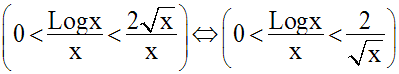
Or, on sait que :
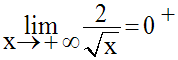
Donc :
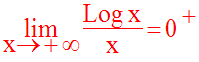
Calculons la limite de la fonction numérique g définie par :
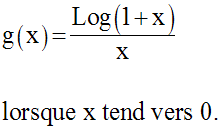

En revenant à la notation en x :
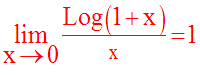
On peut généraliser ce
résultat important en remplaçant x par
une fonction numérique
quelconque tendant vers 0 avec x :
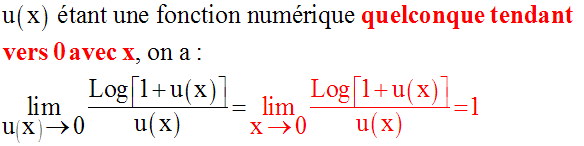
I-e Le nombre e
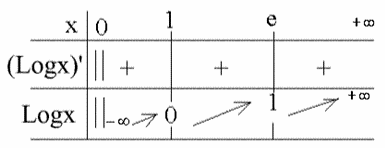
La fonction logarithme népérien est définie, continue, monotone croissante sur R* +.
Elle a pour limite + ∞ lorsque x tend vers + ∞ et pour limite – ∞ pour x tendant vers 0+.
Par suite : l’équation Log x = 1 admet une solution unique.
On note e cette solution. On a donc Log e = 1.
Une valeur approchée de e est 2,718282.
I-f Représentation graphique de la fonction logarithme népérien
Jusqu’à présent, on a déterminé
le domaine de définition ; on a étudié la
monotonie,
les limites en 0+ et en + ∞ de cette
fonction.
Par ailleurs, on peut facilement montrer qu’elle est continue sur son domaine de définition.
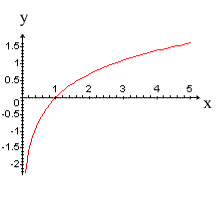
De ces résultats se dégagent donc le tableau de variation de cette fonction, puis sa courbe représentative dans un repère orthonormal .
Sa limite lorsque x tend vers 0+
étant – ∞, sa courbe représentative admet comme asymptote
verticale l’axe des ordonnées.
Par ailleurs, on a :
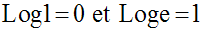
Au point d’abscisse x = 1 de la courbe, la tangente à cette dernière est la droite d’équation :
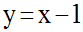
Au point d’abscisse x = e de la courbe, la tangente à cette dernière est la droite d’équation :
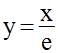
Cette tangente passe donc par l’origine du repère.
Tableau de variation :
Représentation graphique :
II- Fonction exponentielle de base e
II-a Définition et généralités
On a vu précédemment que la
fonction logarithme népérien est définie, continue,
monotone croissante sur R*+.
Il est facile d’en déduire que cette fonction est donc une bijection de R*+ sur R.
La fonction logarithme népérien
admet donc une fonction réciproque, définie sur
R et
dont l’ensemble des valeurs est R*+.
On nomme
fonction exponentielle de base e la fonction
réciproque de la fonction
logarithme népérien.
Notons provisoirement la fonction exponentielle de base e par « exp » .

Elle se lit « exponentielle de x »
On a donc l’équivalence logique suivante :
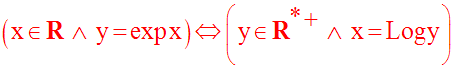
Les propriétés qui suivent
résultent de la bijection
qui a permis de définir la fonction
exponentielle de base e.
a)
La fonction exponentielle de base e est une bijection de R sur R*+.
Il s’ensuit que pour tout réel x, il existe un réel unique, exp x, strictement positif.
b)
La fonction exponentielle de base e est continue et strictement croissante sur R.
c)
Puisque Log 1 = 0, exp 0 = 1.
Puisque Log e = 1, exp 1 = e.
d)
On sait que l’application
composée d’une bijection et de sa réciproque est l’application
identique d’une partie de R sur elle-même :
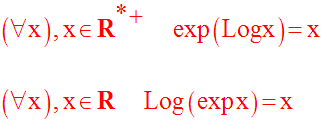
e)
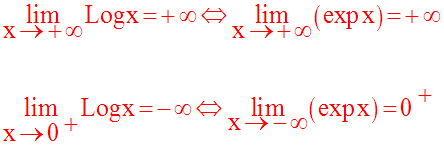
Toutes ces propriétés nous permettent donc de dresser le tableau de variation de la fonction exponentielle de base e et de construire son graphe dans un repère orthonormal.
Exercice
Dresse le tableau de variation de la fonction exponentielle de base e.
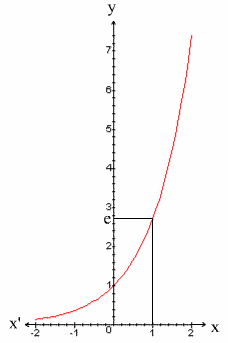
Représentation graphique
On a l’implication suivante :

De plus se graphe est au-dessus de cette asymptote.
Puisque Logx et expx sont
réciproques, leurs graphes sont
symétriques par rapport
à la première bissectrice du repère.
Ces propriétés permettent donc
de construire facilement le graphe de la fonction
exponentielle de base e, à partir de celui de la fonction logarithme népérien.
II-b Propriétés
Propriété fondamentale
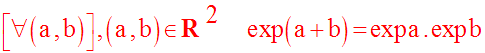
Démonstration
Soient deux réels quelconques a et b et posons c = a + b.
Désignons par α, β et γ les réels uniques, strictement positifs, tels que :
a = Log α, b = Log β, c = Log γ.
C’est-à-dire :
α = exp a, β = exp b, γ = exp c = exp (a + b).
Compte tenu de ces notations, on a :
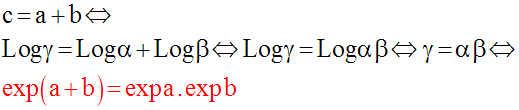
Autres propriétés
On a déjà vu que exp 0 = 1.
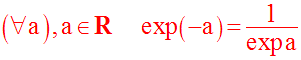
Démonstration
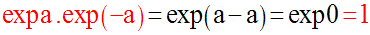
II-c Notation ex
Pour le logarithme népérien
d’une puissance rationnelle d’un réel strictement positif
α, on a établi :
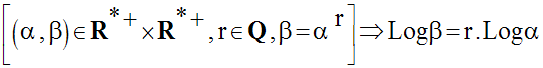
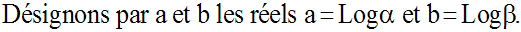
Par définition de la fonction exponentielle de base e, on a :
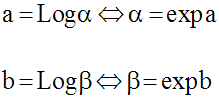
D’où :
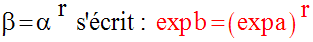
En outre :
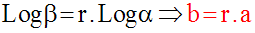
Donc :

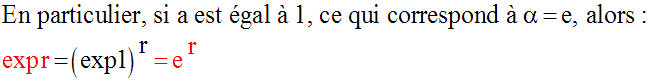
Conclusion :
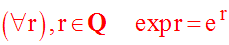
Nous allons étendre cette conclusion à R, pour le seul nombre e.
Par convention et par définition, on a :
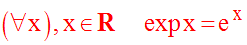
La fonction exponentielle de base e est donc
définie par :
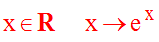
Avec cette nouvelle notation, les propriétés précédemment établies s’expriment comme suit :
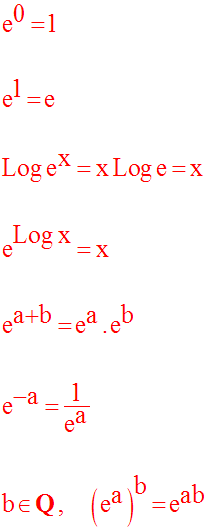
II-d Fonction dérivée de ex
La fonction exponentielle de
base e étant la fonction réciproque de la fonction logarithme
népérien, est dérivable sur R.
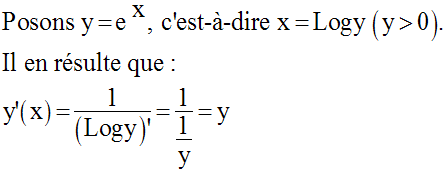
Finalement :
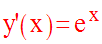
La fonction exponentielle de base e est égale à sa fonction dérivée.
Conséquence :
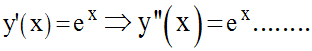
Donc :

La fonction exponentielle de base e est égale à sa dérivée d’ordre n (ou nième).
II-e Recherche de primitives
Sur R, les fonctions
primitives de la fonction exponentielle de base e sont les fonctions
numériques f définies par :
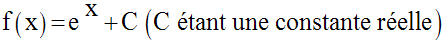
On écrit donc :
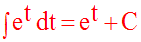
Soit u une fonction numérique, dérivable sur un intervalle réel I.
La fonction g, définie par :
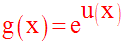
admet pour fonction dérivée sur I la fonction g’ telle que :
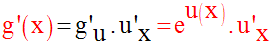
Par conséquent :
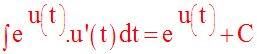
Exemple
Calculons une primitive de la fonction numérique suivante :
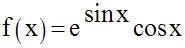
Solution
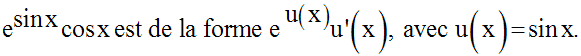
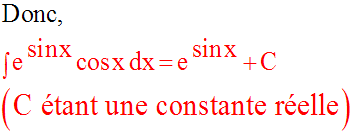
Exercices
1)
Calcule des primitives des fonctions numériques suivantes :
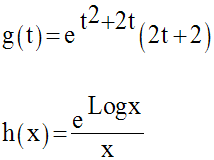
2)
En utilisant une intégration par parties, calcule :
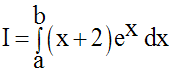
II-f Recherche de limites
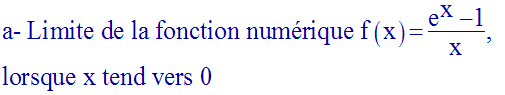
Pour x tendant vers 0, l’expression de f prend la forme indéterminée suivante :
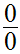
Levons cette indétermination.
Le nombre dérivé de la fonction exponentielle de base e au point 0 est, par définition :
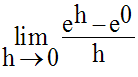
Or, ce nombre dérivé est 1 ; donc on a :
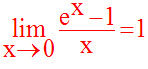
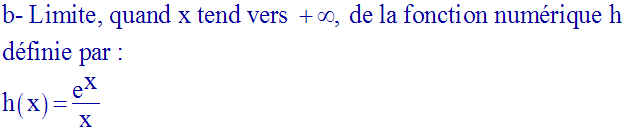
Lorsque x tend vers + ∞ l’expression de h prend la forme indéterminée :
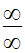
Levons cette indétermination.
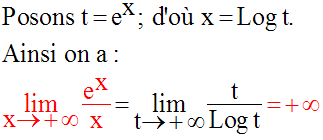
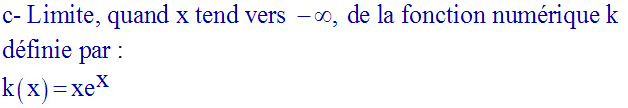
Lorsque x tend vers – ∞, l’expression de k prend la forme indéterminée :
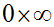
Levons cette indétermination.
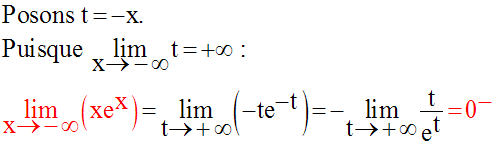
Exercices résolus
Fonction logarithme népérien
1)
Détermine
les limites quand la variable réelle indépendante tend vers + ∞ des fonctions
numériques suivantes :
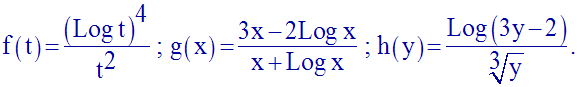
Solution
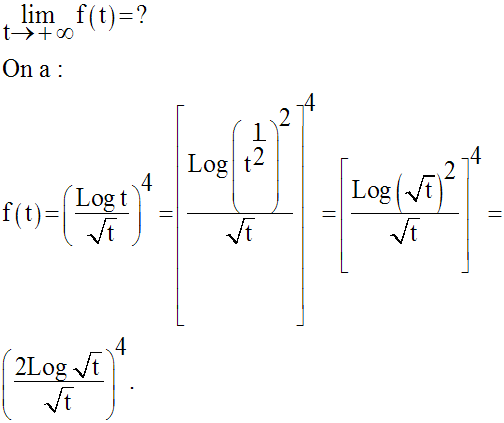
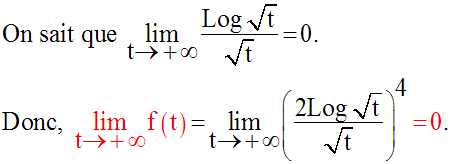

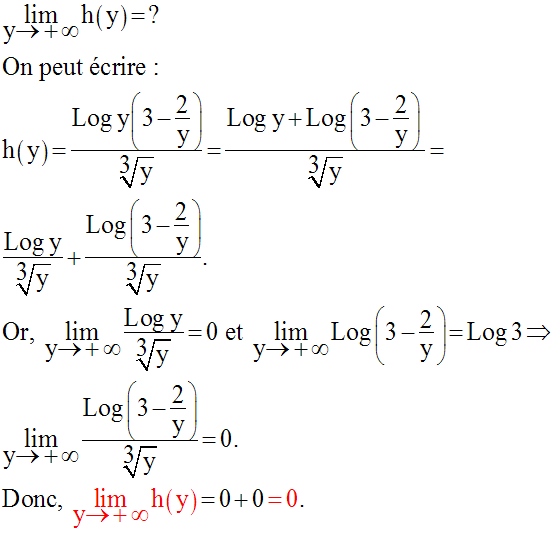
2)
Détermine les limites, quand x tend vers 0, des fonctions numériques suivantes :
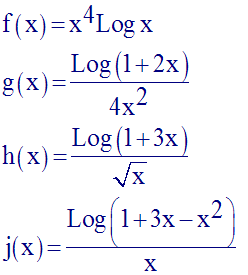
Solution
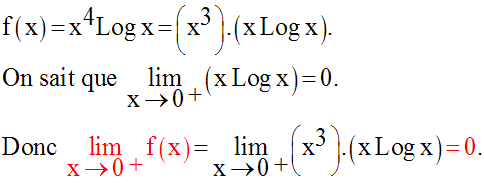
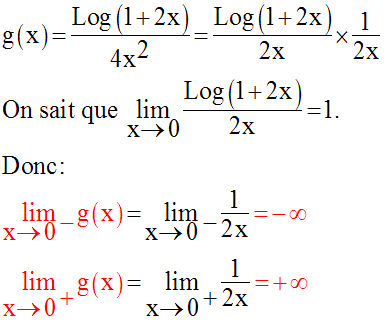
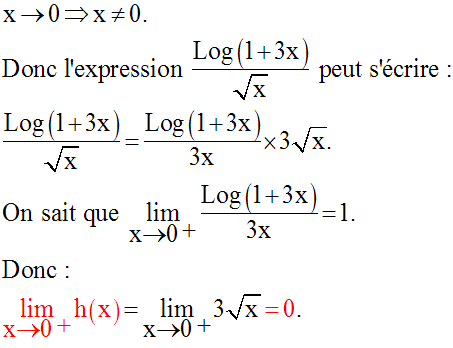
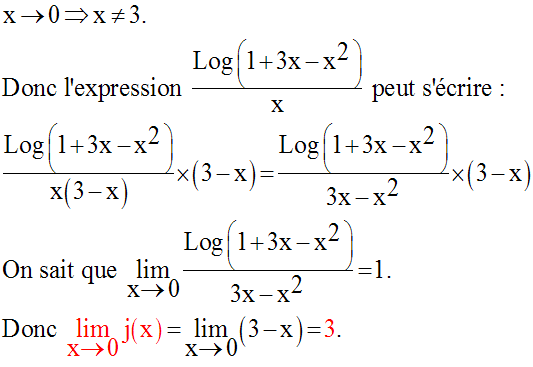
3)
Détermine la limite de la fonction numérique f définie par :

lorsque x tend vers 0 par valeurs supérieures.
Solution
Pour x tendant vers 0, l’expression prend la forme indéterminée 0 × ∞.
Levons cette indétermination en écrivant :
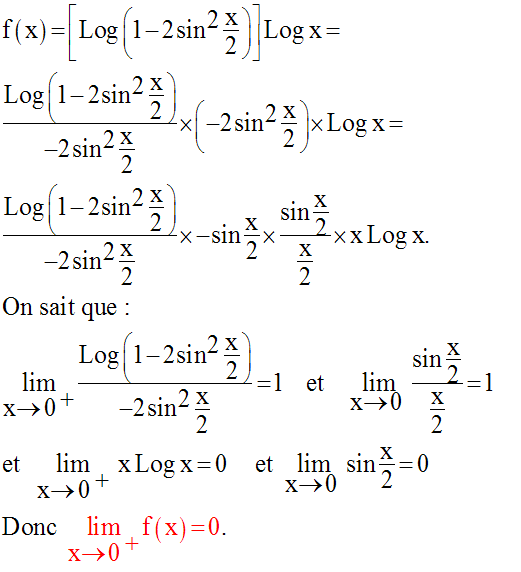
4)
Détermine les limites, quand x tend vers 1, des fonctions numériques suivantes :
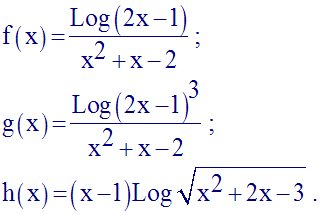
Solution
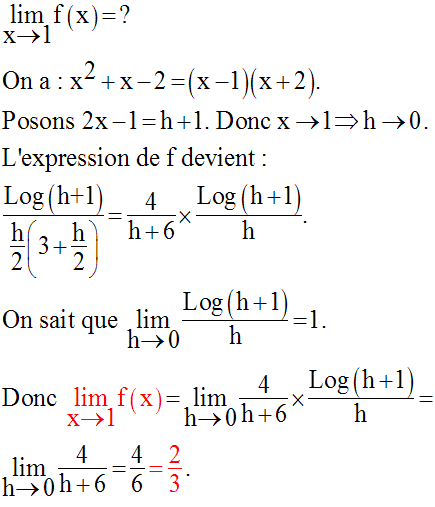
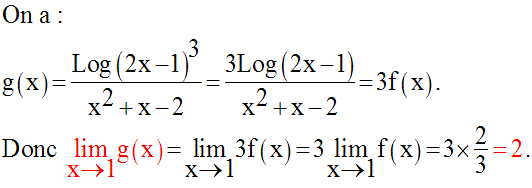

5)
Calcule l’intégrale définie :
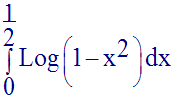
Solution
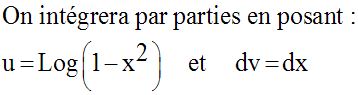
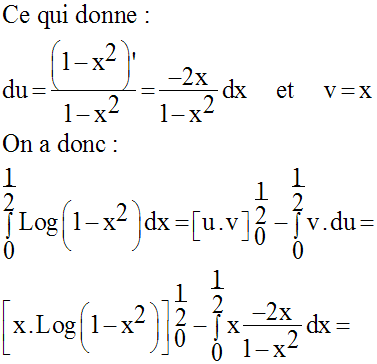
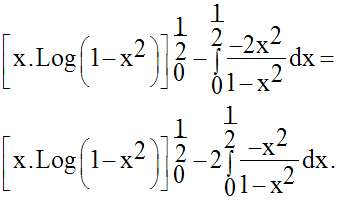
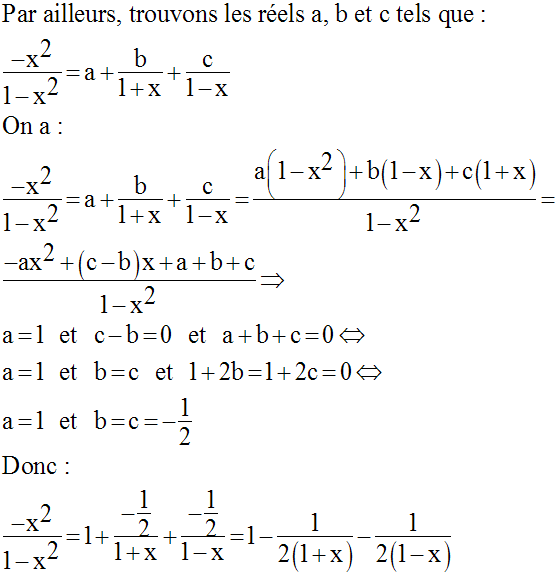
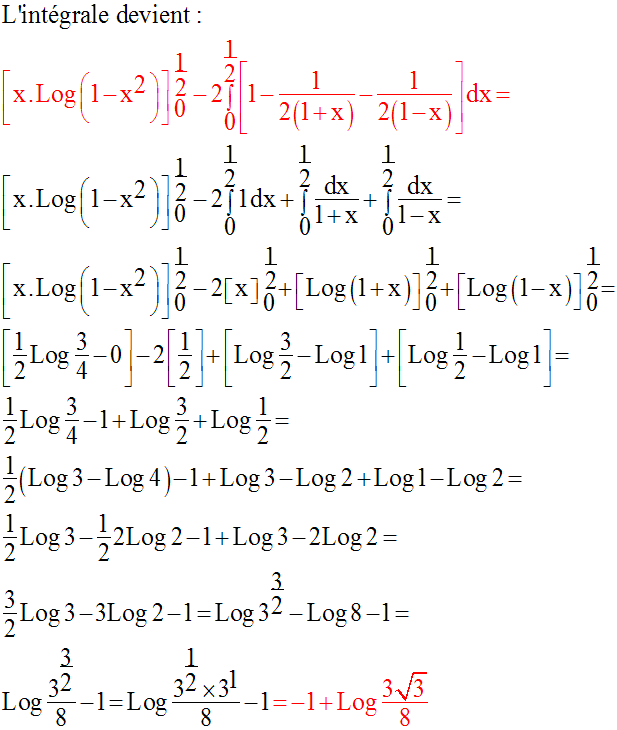
6)
Calcule l’intégrale indéfinie :
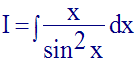
Solution
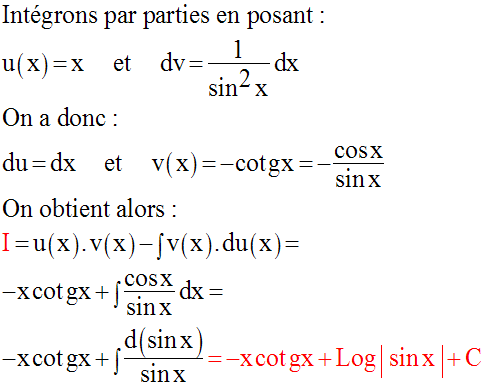
7)
Calcule l’intégrale indéfinie :
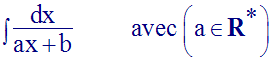
Solution
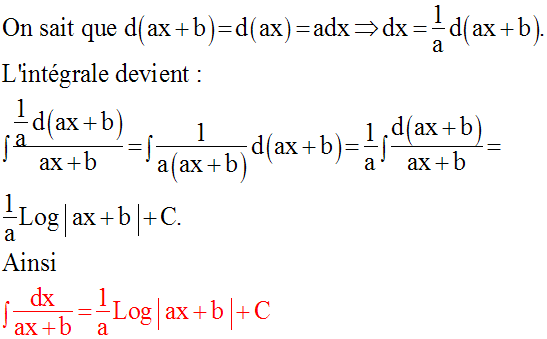
8)
Résous dans R l’équation suivante :
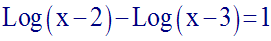
Solution
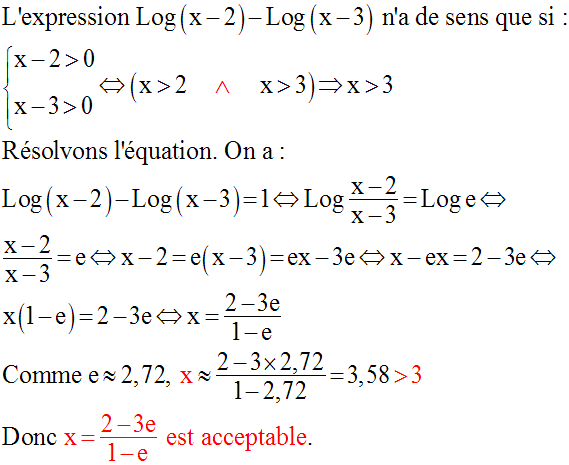
9)
Résous dans R l’équation :
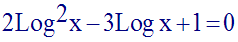
Solution

10)
Résous dans R l’équation :
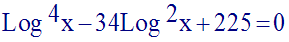
Solution
Notons d’abord que l’expression
du premier membre n’a de sens que si le réel x est
strictement positif ; donc il faut que x soit strictement positif.
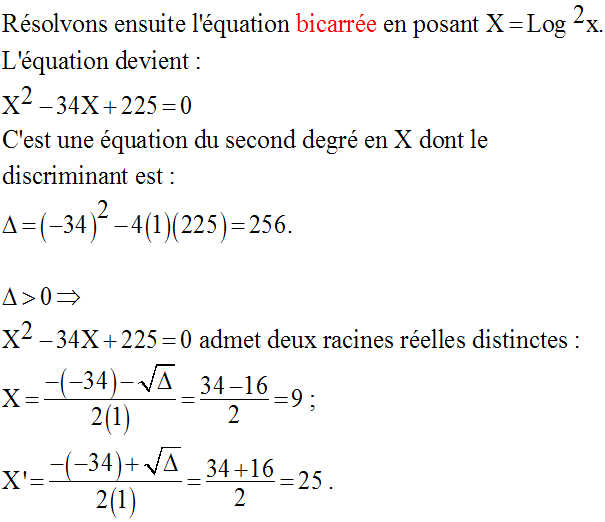
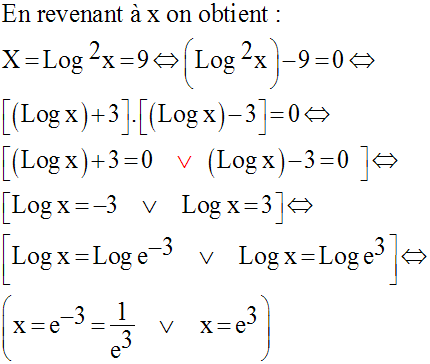
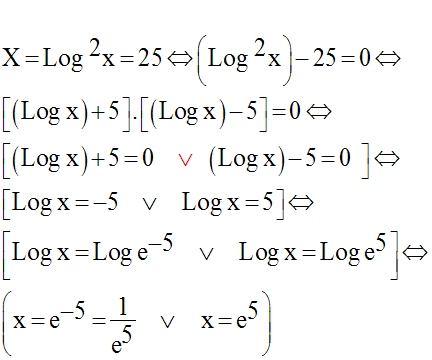

11)
Résous dans R2 le système :
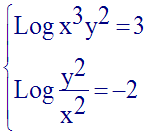
Solution

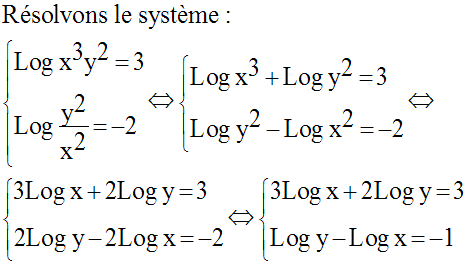
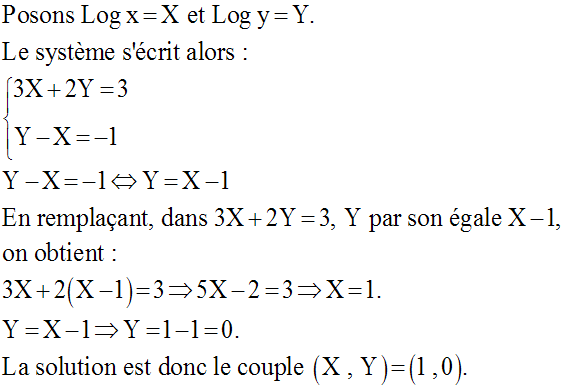

12)

Solution
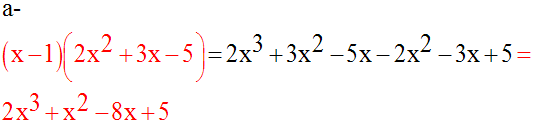
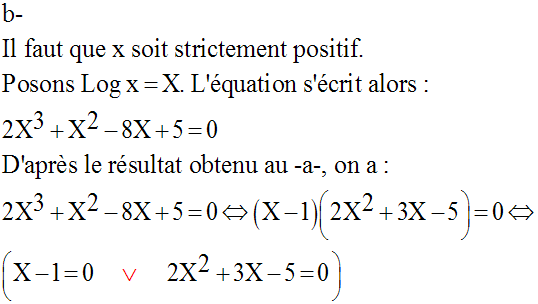
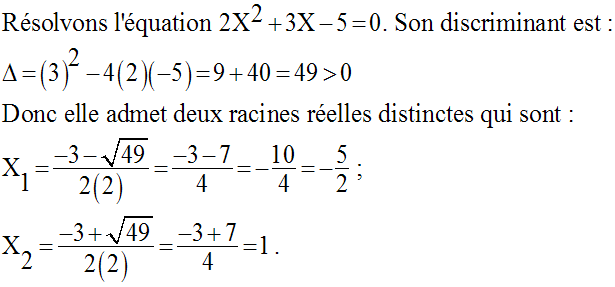
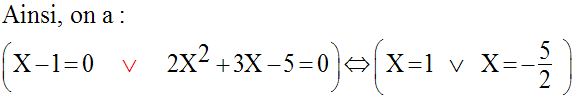

13)
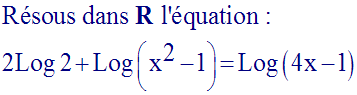
Solution
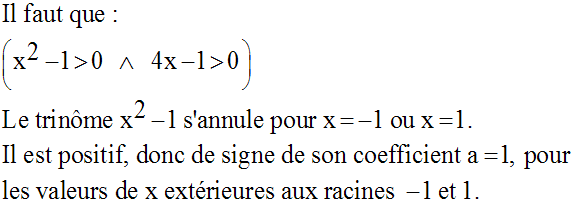
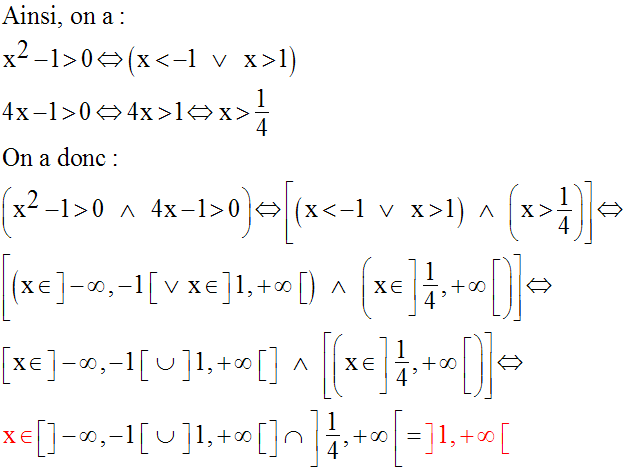
Résolvons l’équation :

14)
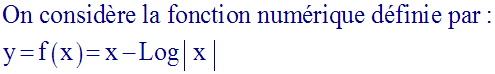

Solution
a-
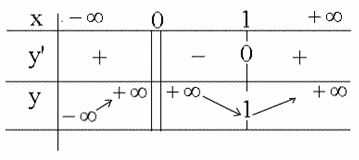
Le domaine de définition de f est R*.
f est continue sur son domaine de définition.
La dérivée de f est :
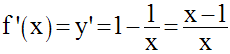
Elle est nulle pour x = 1, strictement positive pour x < 0 ou
x > 1 et strictement négative pour 0 < x < 1.

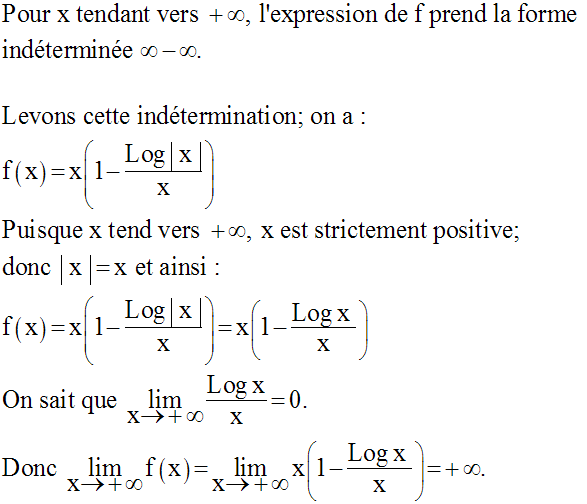
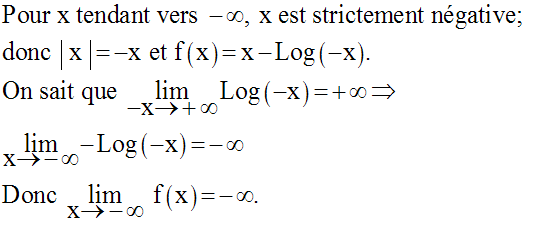
D’où le tableau de variation de f :
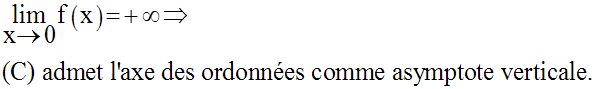
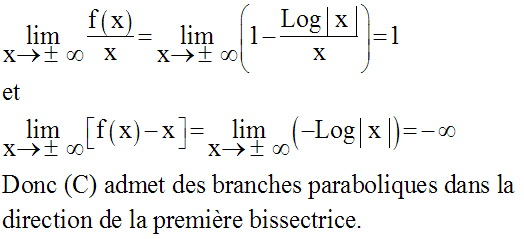
D’où la construction de (C) :
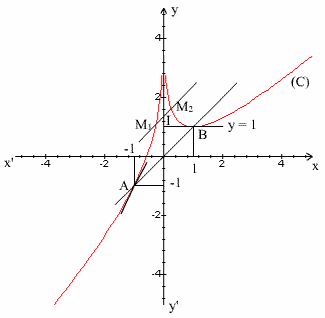
b-
Les abscisses des points
d’intersection M1 et M2 de (C) et de la droite d’équation
y = x + m doivent vérifier l’équation aux abscisses :
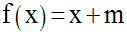
On a donc :
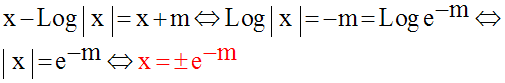
Il y a donc, pour
toute valeur du paramètre réel m, deux points d’intersection M1 et M2
de (C) et de la droite d’équation y = x + m d’abscisses respectives :
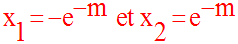
De plus, on a, pour tout m :
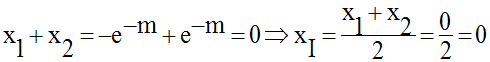
L’ensemble des positions du milieu I de [M1M2] est l’axe des ordonnées.
Pour m nul, on a :
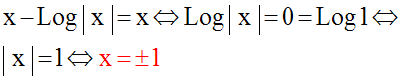
Les abscisses des points
d’intersection A et B de (C) avec la première bissectrice sont
respectivement – 1 et 1.
Comme ces points appartiennent à la première bissectrice, on a :
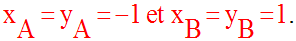
La tangente en B à (C)
est parallèle à l’axe des abscisses.
La tangente en A à (C) a pour pente 2.
Enfin ces deux tangentes se coupent sur l’axe des
ordonnées.
15)
Résous dans R l’inéquation :
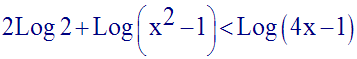
Solution
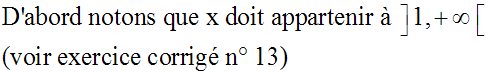
Résolvons l’inéquation :
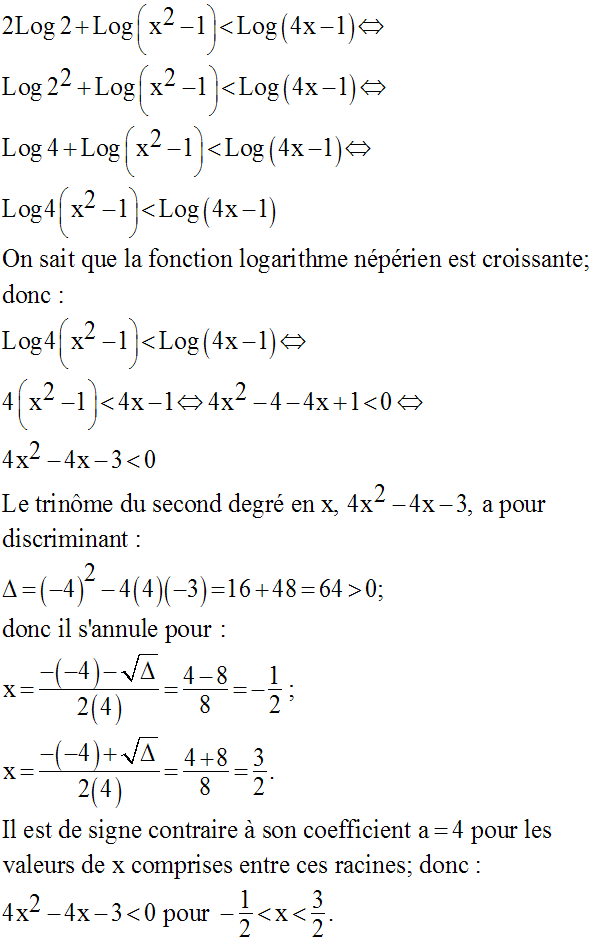
Conclusion
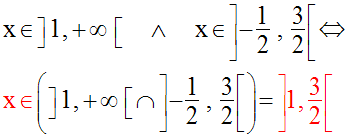
Fonction exponentielle de base e
1)
Dans R, discute, suivant les valeurs du paramètre réel m, le nombre des racines de l’équation :
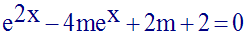
Résous cette équation dans le cas où m = 1.
Solution
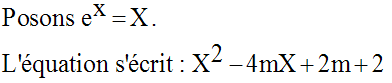

Le discriminant Δ de l’équation est :
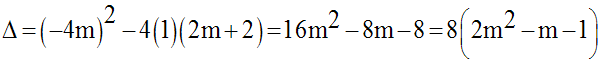
On sait que le nombre des
racines de l’équation donnée dépend du signe de ce discriminant
et à la condition que toute racine soit strictement positive.
Donc trois cas à étudier : Δ < 0 ; Δ = 0 ; Δ > 0

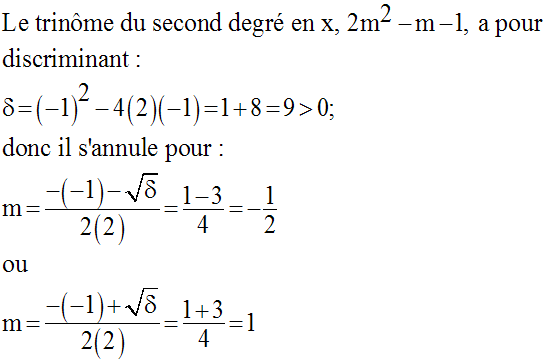

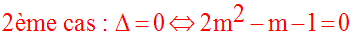


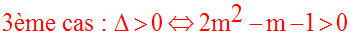

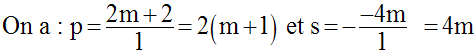
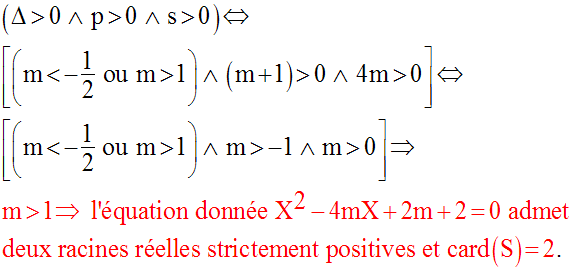
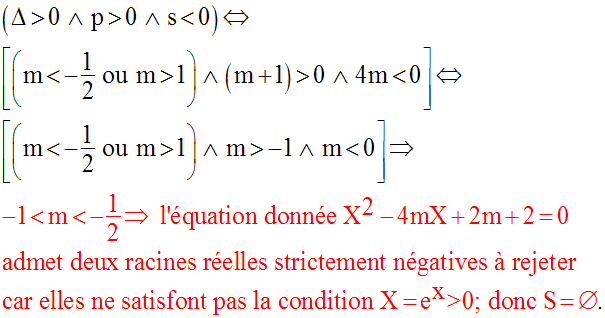

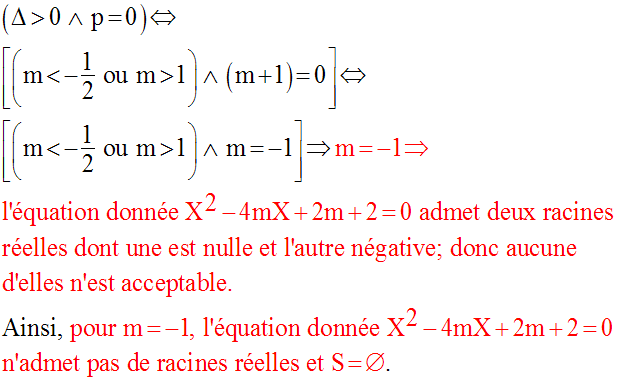
On a vu que pour m = 1, l’équation donnée admet pour racine réelle X = 2.
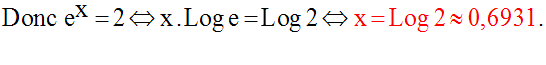
2)

Solution
Pour x tendant vers 0, l’expression de cette fonction numérique prend la forme indéterminée :
Levons cette indétermination.
On sait que x tendant vers 0, x
et x3 sont donc différents de 0 ; on peut alors multiplier
les deux membres de la fraction définissant f par x3 ; il vient :
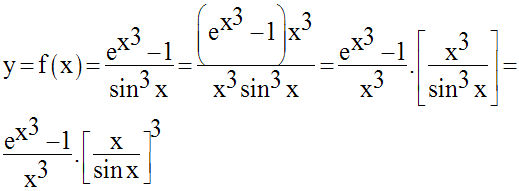
On sait que (voir plus haut : II-f Recherche de limites) :
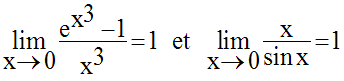
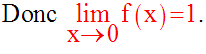
3)
Détermine la limite, quand x tend vers 0, de la fonction numérique :
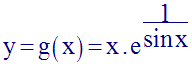
Solution
L’exposant de e est fonction de
sin x ; donc son signe dépend de la manière par laquelle
x tend vers 0.
Deux cas sont à envisager :

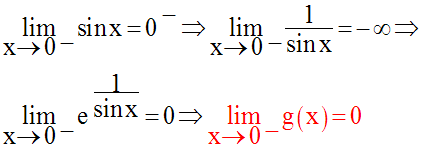
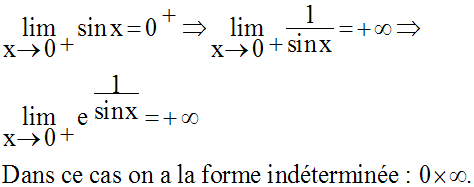

4)

Solution

5)
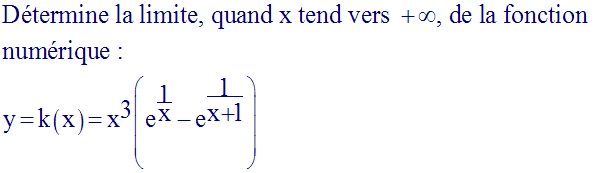
Solution

On sait que :

6)

Solution
Calculons les deux premières dérivées ; on a :

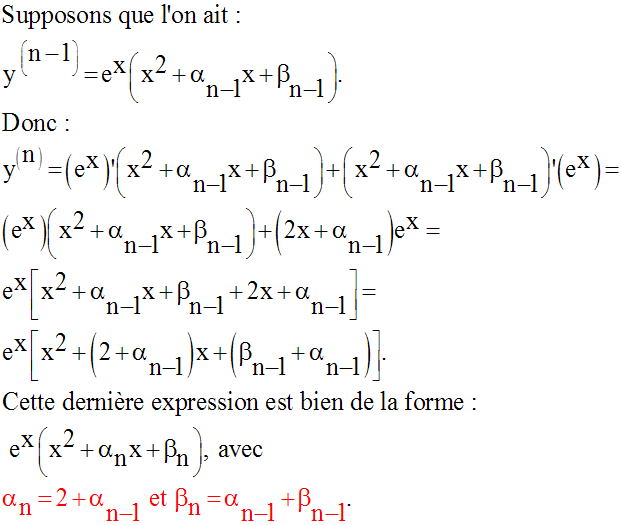
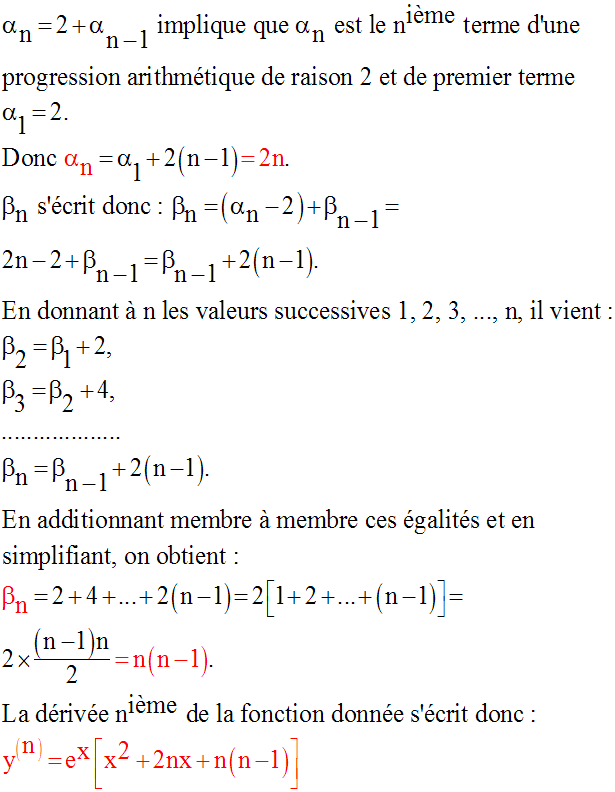
7)
Calcule les intégrales indéfinies suivantes :
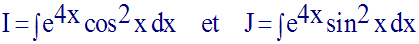
Solution
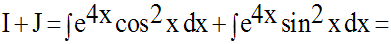
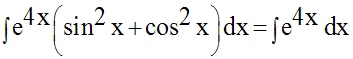
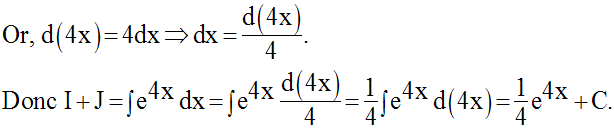
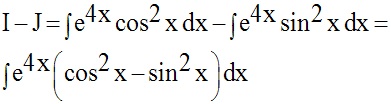
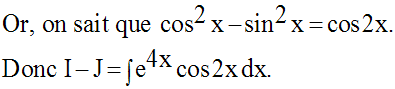
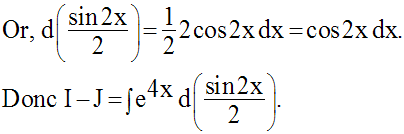
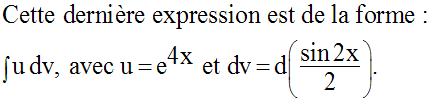
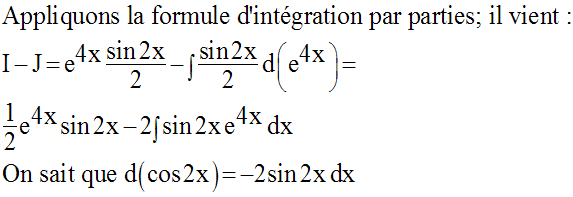
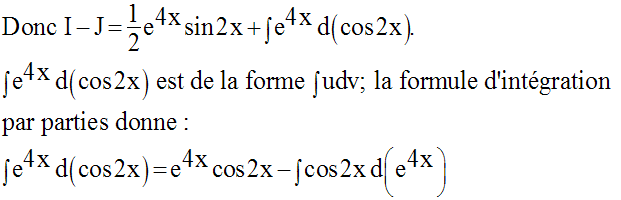
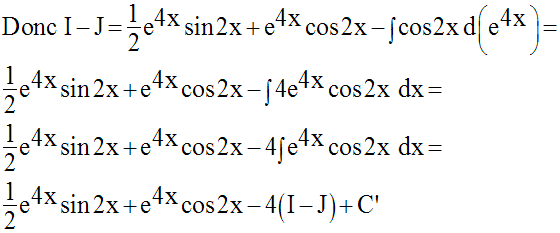
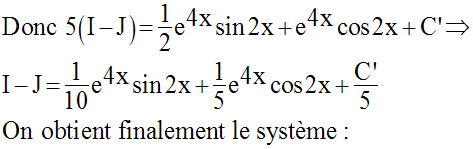
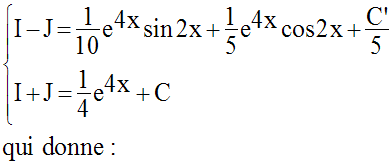
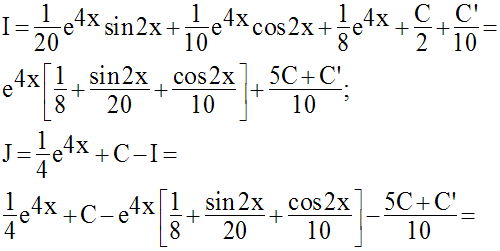
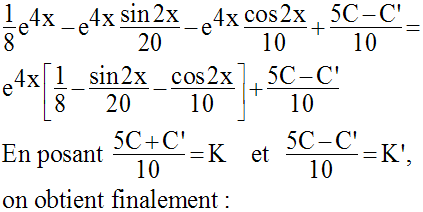
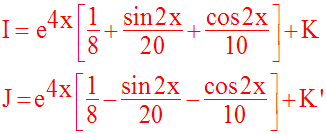
8)
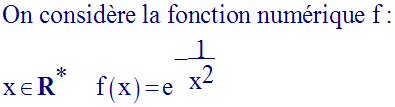
a-
Quelle valeur faut-il donner à f (0) pour que cette fonction numérique soit continue sur R ?
b-
On prend
pour f (0) la valeur obtenue précédemment.
Montre que, dans ces conditions, f est dérivable pour x = 0.
Cette dérivée est-elle continue au point 0 ?
Solution
a-
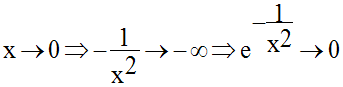
Ainsi, f est continue en x = 0 si l’on prend f (0) = 0.
Finalement la fonction numérique f est définie comme suit :
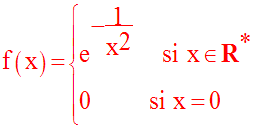
f est ainsi définie et continue sur R.
b-
Pour montrer que f est dérivable en 0, il suffit de s’assurer que l’expression :
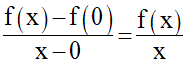
admet une limite réelle finie lorsque x tend vers 0.
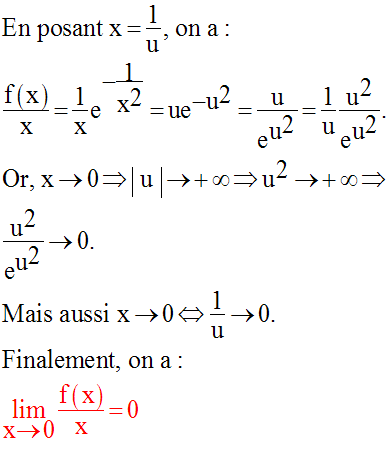
f est donc dérivable en 0 et sa dérivée au point 0 a pour valeur f ’(0) = 0.
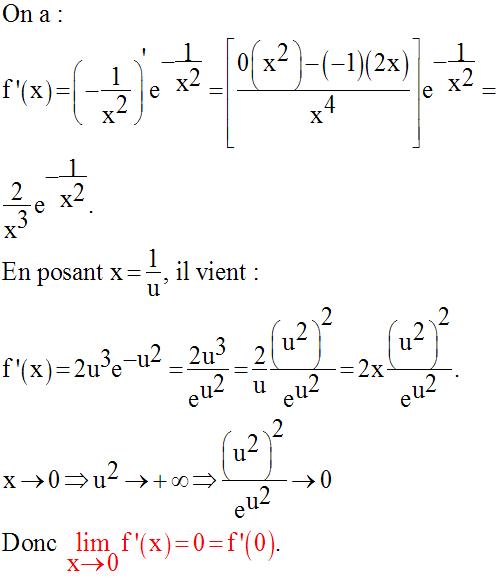
La fonction dérivée de f est donc continue en 0.
9)
Montre à l’aide d’une brève étude de la fonction numérique f définie par :
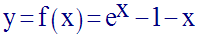
que l’on a :
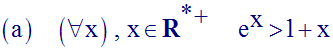
En déduis que l’on a également :
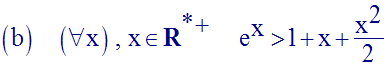
et, plus généralement, pour tout entier positif n,
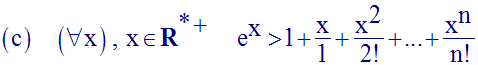
En déduis que :
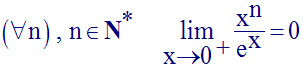
Solution
f est définie et continue sur R.
Sa dérivée est :
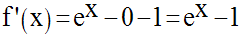
Cette dérivée s’annule pour x = 0 et est strictement positive pour tout réel x strictement positif.
Donc f est strictement croissante sur R+.
Mais comme f (0) = 0, alors f est strictement positive sur R* + ; ainsi :
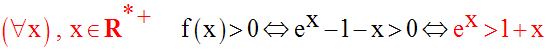
Considérons la fonction numérique g définie par :
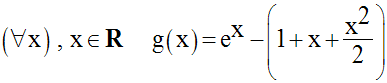
g est définie et continue sur R.
Sa dérivée est :
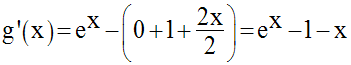
Cette dérivée s’annule pour x =
0 et, d’après ce qui précède, est strictement positive
pour tout réel x strictement positif.
Donc g est strictement croissante sur R+.
Mais comme g (0) = 0, alors g est strictement positive sur R* + ; ainsi :
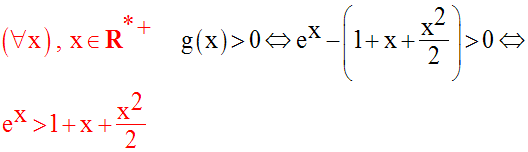
Raisonnons par récurrence sur n, entier positif, et supposons que l’on a :
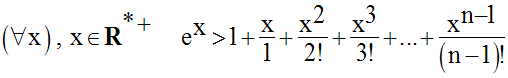
Soit la fonction numérique u définie par :
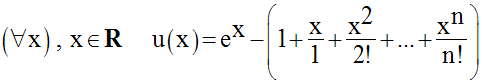
u est définie et continue sur R.
Sa dérivée est :
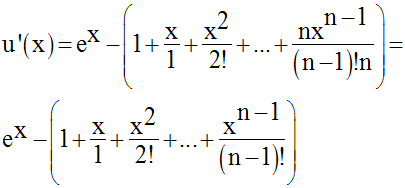
Compte tenu de l’hypothèse ,
cette dérivée, qui s’annule pour x = 0, est strictement
positive pour tout réel x strictement positif.
Donc u est strictement croissante sur R+.
Mais comme u (0) = 0, alors u est strictement positive sur R* + ; ainsi :
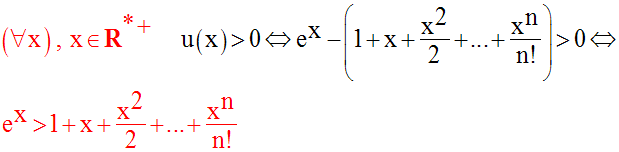
On a :
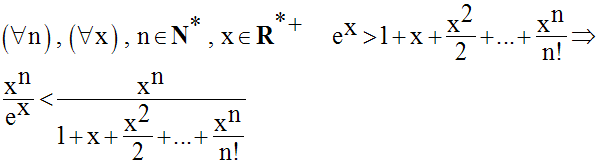
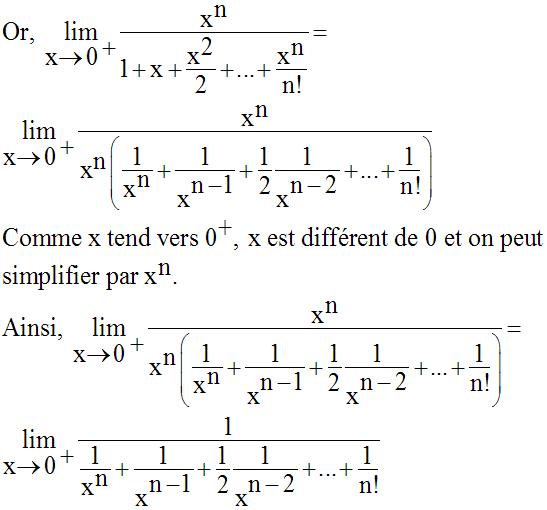

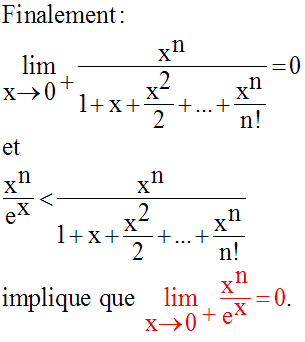
10)

Solution
a-
On a :
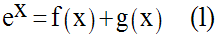
Comme f est paire et g, impaire, en substituant dans cette relation x par –x, on obtient :
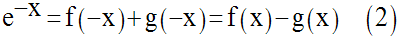
Additionnons et soustrayons membre à membre les relation (1) et (2) ; il vient :
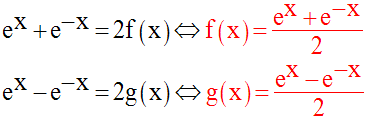
b-
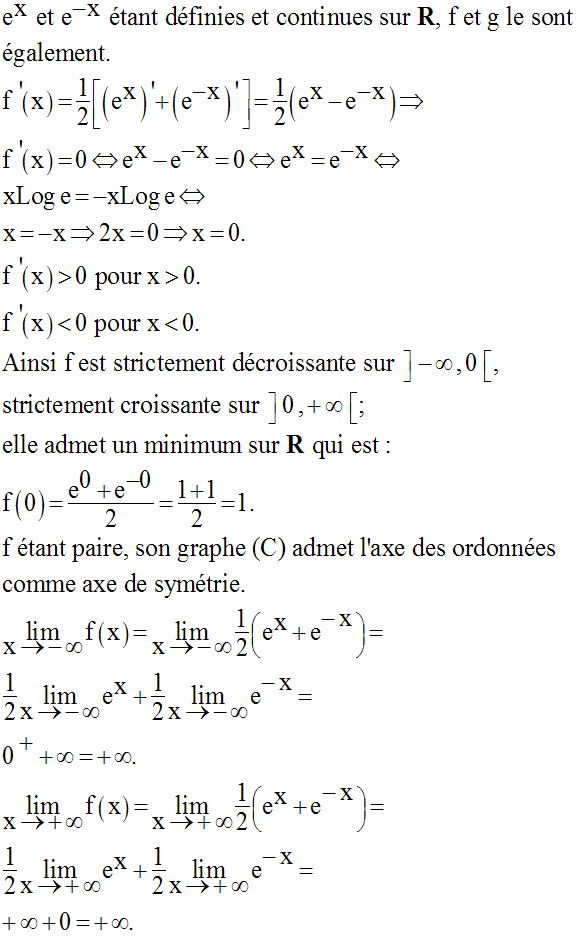
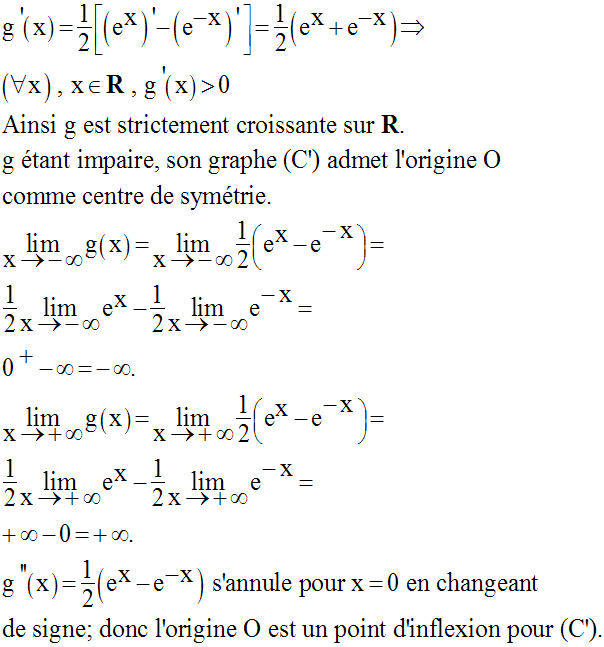
Les variations de f et g sont résumées dans le même tableau qui suit :
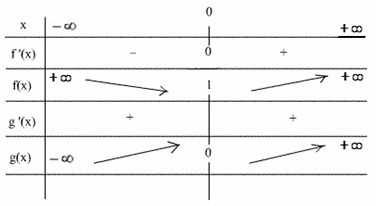
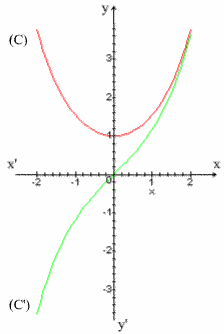
Construction de (C) et de (C’) :
On a :
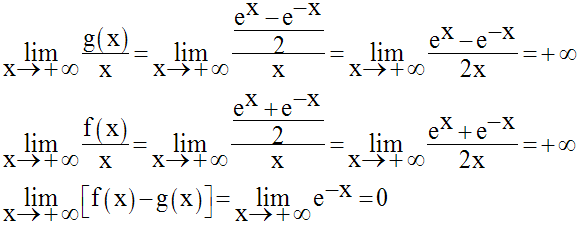
Ceci implique que (C) et (C’)
ont des branches paraboliques dans la direction de l’axe
des ordonnées et sont asymptotes l’une à l’autre pour les
valeurs infinies positives de x.
c-
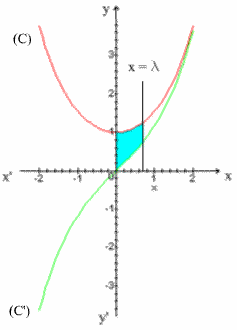
l’aire S(λ) du domaine considéré (en bleu sur la figure) est égale à :
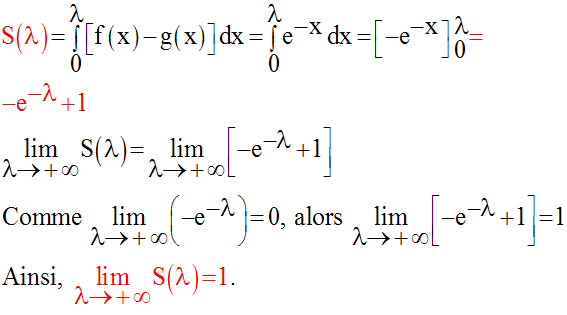
11)
Calcule l’intégrale indéfinie :
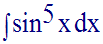
Solution
Rappelons les formules d’Euler :
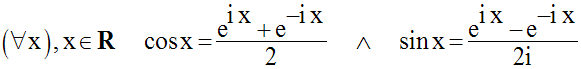
Ainsi, on a :
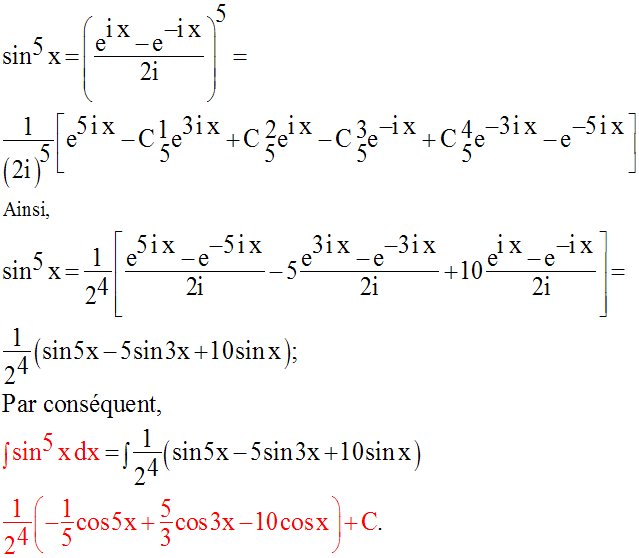
Exercices non résolus
Fonction logarithme népérien
1)
Résous dans R les équations suivantes :
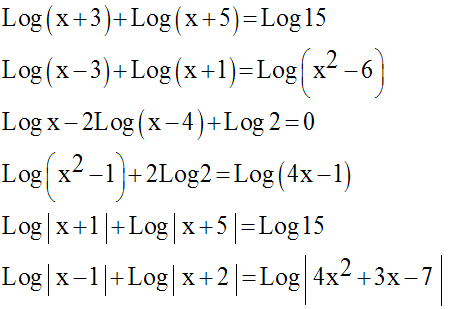
Directives :
Avant de
commencer à résoudre une équation, il faudra trouver son domaine de définition,
sachant que pour les valeurs réelles données à la variable x et rendant une
quantité, sous Log, largement négative, sont à
rejeter.
2)
Résous dans R2 les systèmes suivants :
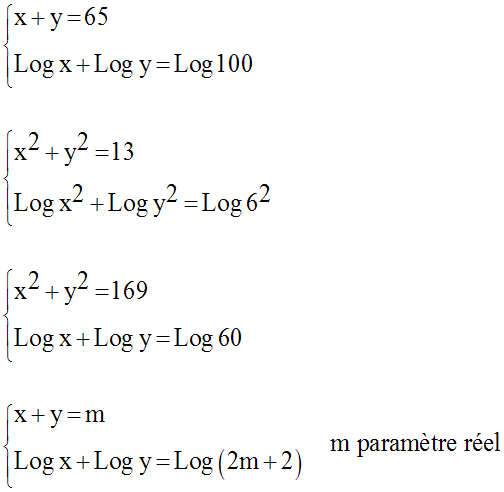
Directives :
Avant de commencer à résoudre
une équation, il faudra trouver son domaine de définition,
sachant que pour les valeurs réelles données à la variable x et rendant une
quantité, sous Log, largement négative, sont à
rejeter.
3)
Calcule les fonctions dérivées des fonctions numériques suivantes :
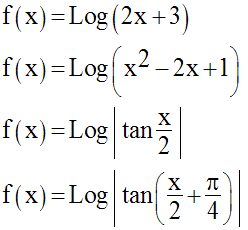
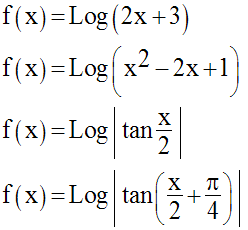
Directives :
Préalablement au calcul de la dérivée, il faudra déterminer le domaine de définition de la fonction numérique donnée.
4)
En utilisant la dérivée logarithmique, calcule les fonctions dérivées des fonctions numériques suivantes :
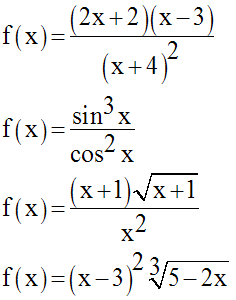
Directives :
Préalablement au calcul de la dérivée, il faudra déterminer le domaine de
définition de la fonction numérique donnée.
5)
Calcule les fonctions primitives des fonctions numériques suivantes :
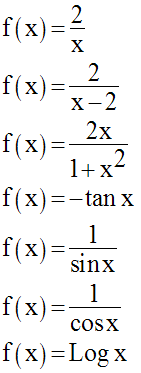
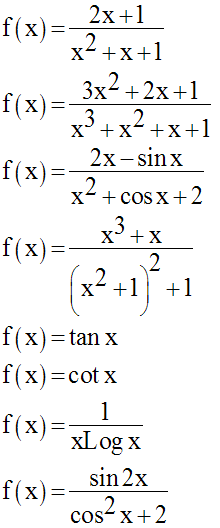
6)
En utilisant l’intégration par parties, calcule les primitives des fonctions numériques suivantes :
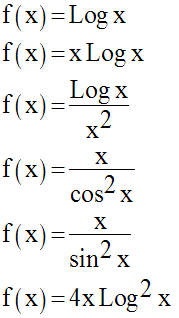
7)
Trouve la limite de la fonction numérique f lorsque x tend vers + ∞ :
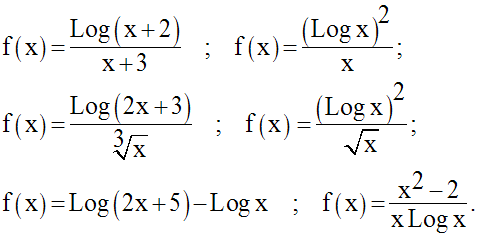
8)
Résous dans R l’inéquation suivante :
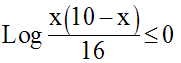
9)
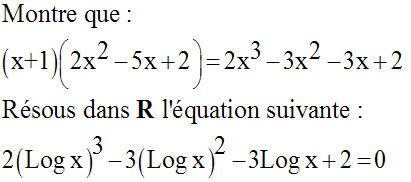
10)

11)

12)

13)
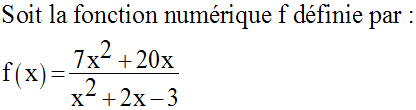
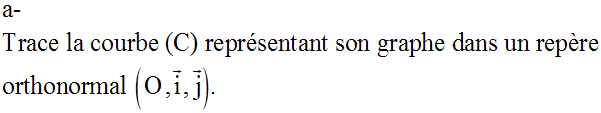
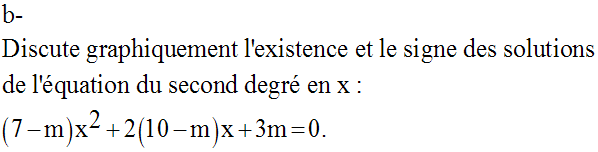


14)



Fonctions exponentielles de base e
1)
On donne les deux fonctions numériques :
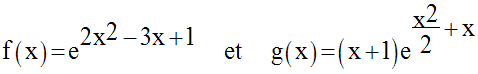
Calcule :
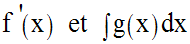
2)
Résous dans R les équations suivantes :
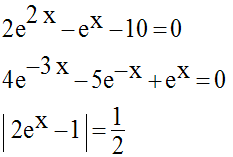
3)
On donne la fonction numérique :
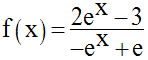
Trouve son domaine de définition et calcule l’expression de sa dérivée.
4)
Discute graphiquement, suivant les valeurs du paramètre réel m, le nombre de racines de l’équation :
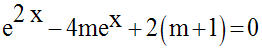
(on prendra un repère orthonormal)
5)
Etudie les variations et construis le graphe de la fonction numérique f définie par :
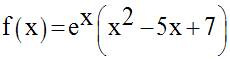
6)
Calcule les deux intégrales indéfinies :
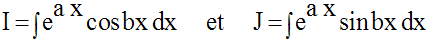
7)

8)
On considère la fonction numérique f définie par :
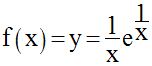
a-
Détermine la limite de f dans chacun des cas suivants :
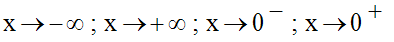
b-
Etudie les variations de f et
construis, dans un repère orthonormal, sa courbe représentative (C).
On précisera la tangente au point O, origine du repère.
c-
Soit (D) le domaine limité par
le demi axe [Ox’ des abscisses négatives et l’arc de (C) qui
correspond à x largement négative.
Calcule le volume, V, engendré par (D) tournant autour de
[Ox’.