LES FONCTIONS LOGARITHME  ET EXPONENTIELLE
DE BASE a (a réel strictement positif)

I- Fonction logarithme de base a (a réel strictement positif et différent de 1)

I-a Définition

Soit a un réel strictement positif et différent de 1 quelconque.

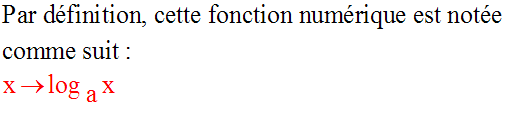
On remarque bien que, contrairement à la fonction logarithme népérien,
cette fois le symbole « log » est en « l minuscule » et porte en indice le réel
strictement positif a.

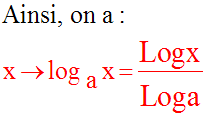
I-b Etude et propriétés

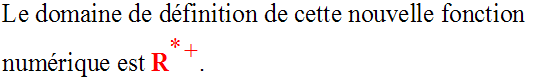
Ainsi on a :

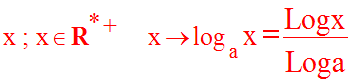
Cette nouvelle fonction est une bijection de R^{* +} sur R.

Pour a = e, on retrouve le cas particulier de la fonction logarithme népérien ;
en effet :

Si a = 10, alors la fonction logarithme à base 10 est appelée fonction logarithme
décimal.

On la note :

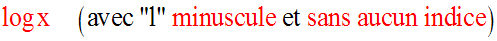
Remarque importante

Au baccalauréat, à l’épreuve de Mathématiques, et au départ de la résolution d’un
exercice ou d’un problème, confondre log (avec l minuscule) et Log (avec L majuscule)
est une erreur fatale aboutissant à l’échec à cette épreuve.

On peut trouver l’égalité qui permet de passer d’un logarithme de base a (a strictement positif
et différent de 1) quelconque à un logarithme de base b (b strictement positif, différent de 1
et de a), quelconque.

En particulier, pour a = e et b = 10,

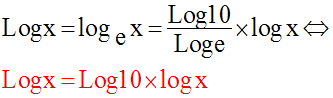
C’est cette dernière relation qui permet de convertir un logarithme népérien en logarithme
décimal et vice versa.

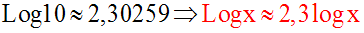
La fonction logarithme népérien Logx étant continue et dérivable sur R^{* +} , la fonction
logarithme de base a :

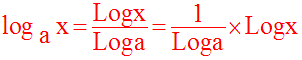
est également continue et dérivable sur son domaine de définition.

Comme x est toujours strictement positif, le signe de la dérivée dépend de celui de Loga.

Etude des limites de la fonction logarithme de base a, a réel strictement positif
et différent de 1

Deux cas à envisager :

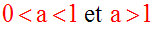
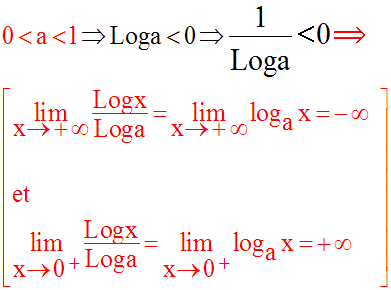
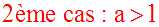
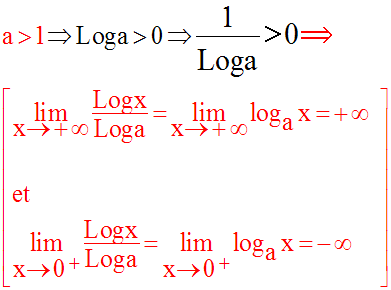
Particularités du graphe de la fonction logarithme de base a, avec a réel strictement positif, différent de 1 et de e

L’étude de la limite en zéro montre que ce graphe admet pour asymptote verticale l’axe des ordonnées.

Dans la suite, le repère sera supposé orhonormal.

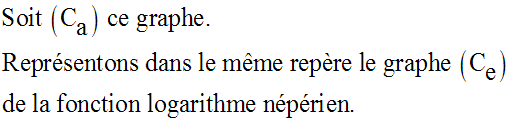
Soit D une droite quelconque parallèle à l’axe ses ordonnées, rencontrant (C_a), (C_e) et
l’axe des abscisses respectivement aux points A, E et H.

On a :

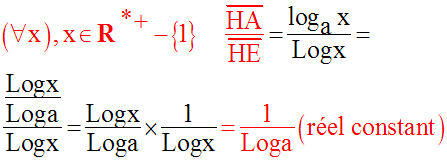
Ainsi, le graphe de la fonction logarithme de base a, a strictement positif différent de 1
et de e, se déduit de celui de la fonction logarithme népérien par une affinité orthogonale
d’axe celui des abscisses, de direction celle de l’axe des ordonnées et de rapport :

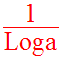
Enfin, l’équation en x :

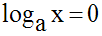
admet une seule racine x égale à 1.

Tous les graphes des fonctions logarithmes de base a passent par le point de l’axe des abscisses, d’abscisse 1.

L’étude des variations de la fonction logarithme de base a, du signe de sa dérivée, de ses
limites en zéro et à l’infini, ainsi que les particularités du graphe vues précédemment,
permettent de tracer ce dernier avec facilité.

II- Fonction exponentielle de base a (a réel strictement positif et différent de 1)

II-a Définition

Soit a réel strictement positif et différent de 1, quelconque.

On a vu que la fonction logarithme de base a est définie, continue et strictement
monotone sur son domaine de définition. On a vu également qu’elle est une bijection
de R^{* +} sur R.

Par conséquent, elle admet une fonction réciproque, définie sur R et prenant ses
valeurs dans R^{* +}.

Cette fonction réciproque se nomme fonction exponentielle de base a.

Provisoirement, on la notera :

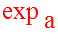
Ainsi, on a l’équivalence logique suivante :

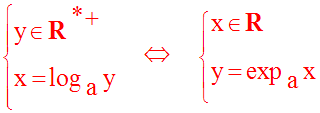
II-b Etude et propriétés

Les propriétés qui suivent résultent de la bijection log_a de R^{* +} sur R.

La fonction exp_a est une bijection de R sur R^{* +}.

Il en résulte que pour tout réel x, il existe au moins un réel, exp_a x, et un seul,
strictement positif.

La fonction exponentielle de base a est continue et strictement monotone sur R.

Si a > 1, alors elle est strictement croissante.

Si 0 < a < 1, alors elle est strictement décroissante.

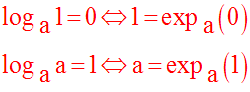
En composant la bijection log_a avec sa réciproque exp_a on obtient l’application
identique Id d’une partie de R sur elle-même :

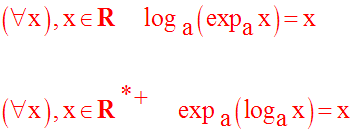
Autre expression de la fonction exponentielle de base a

On a par définition :

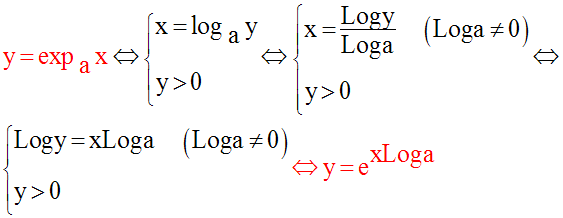
Toute exponentielle de base a peut s’exprimer par une exponentielle de base e.

C’est une propriété très importante puisqu’elle permet, dans tout problème faisant
intervenir une exponentielle de base a, de traiter cette dernière à l’aide d’une
exponentielle de base e.

Propriété fondamentale

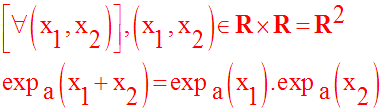
Démonstration

D’après ce qui précède, on a :

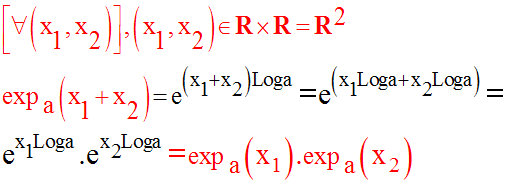
Autres propriétés

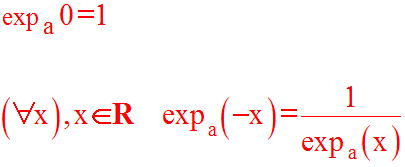
Cette dernière propriété est facile à établir en utilisant encore l’égalité :

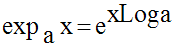
Nouvelle notation de la fonction exponentielle de base a

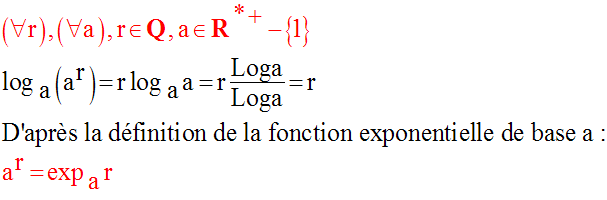
Cette égalité étant vraie pour tout r rationnel, on l’étend à l’ensemble R des réels
en écrivant, par définition :

Ainsi, on a la fonction exponentielle de base a, définie comme suit :

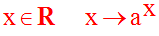
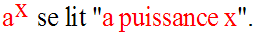
On a également l’égalité importante :

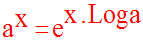
En utilisant cette nouvelle notation, on peut écrire :

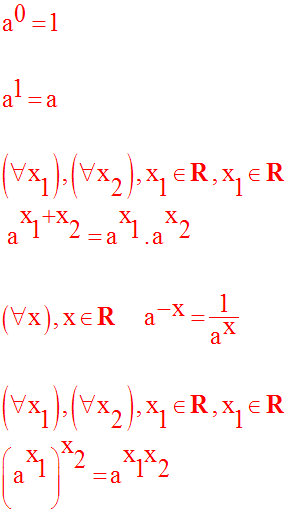
Démontrons la dernière égalité.

On a :

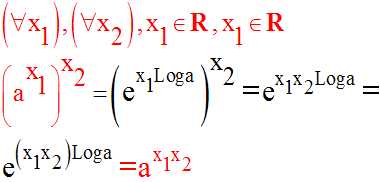
Etude de la fonction exponentielle de base a

Plus haut, on a vu que cette fonction est définie pour tout réel x, continue et strictement
monotone sur R.

L’étude des limites se fait en envisageant les deux cas :

a > 1 et 0 < a < 1

Cette étude permet de conclure que le graphe de la fonction exponentielle de base a
admet, quel que soit le repère, pour asymptote horizontale, l’axe des abscisses.

Fonction dérivée de la fonction exponentielle de base a

On pose :

La dérivée ne s’annule pour aucun réel x.

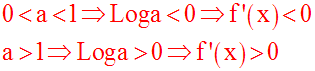
Ainsi f est strictement croissante pour a strictement supérieur à 1 et strictement
décroissante pour a strictement inférieur à 1.

Enfin, pour la valeur de x égale à 0, son image est a⁰ = 1.

L’étude des variations de la fonction exponentielle de base a, du signe de sa dérivée,
de ses limites aux infinis, permettent de tracer ce dernier avec facilité.

On suppose que le repère est orthonormal.

La fonction exponentielle de base a étant la fonction réciproque de la fonction
logarithme de base a, leurs graphes sont symétriques par rapport à la première
bissectrice du repère.

II-c Recherche de fonctions primitives

Soit la fonction numérique f définie comme suit :

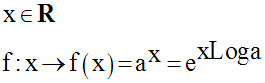
f admet pour fonction dérivée :

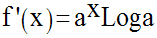
Par conséquent, la fonction numérique g, définie par :

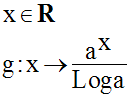
admet pour fonction dérivée g’, telle que :

Les fonctions primitives de la fonction exponentielle de base a sont donc F telles que :

On peut également écrire :

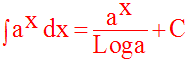
III- Fonction numérique de la forme u(x)^v(x)

u et v sont deux fonctions numériques quelconques.

On pose :

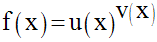
On admettra l’égalité suivante :

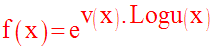
Cette égalité étant admise, on doit ensuite trouver le domaine de définition, dom(f).

f n’est définie que si u(x) est strictement positive.

Ainsi,

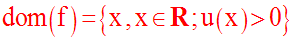
Fonction dérivée de f

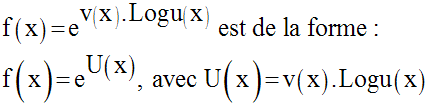
Or, on sait que :

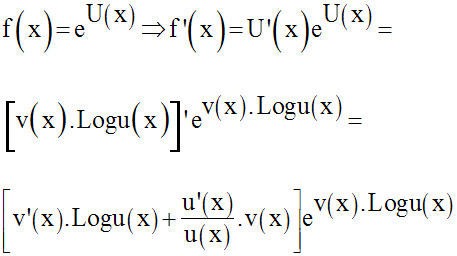
On obtient finalement, avec x quelconque appartenant à dom(f) :

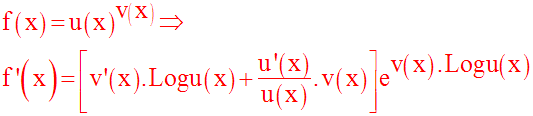
L’étude du signe de cette dérivée permettra de déduire les variations de f.

Par ailleurs, les limites de f seront étudiées en utilisant l’écriture :

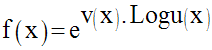
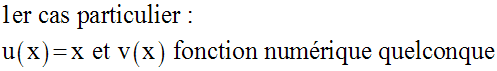
f s’écrit donc :

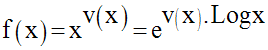
Son domaine de définition est donc :

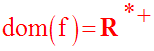
Sa fonction dérivée est :

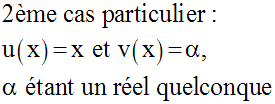
f s’écrit donc :

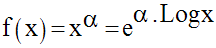
Son domaine de définition est donc :

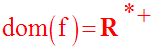
Sa fonction dérivée est :

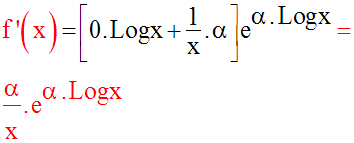
Exercices

1)

Résous dans R les équations suivantes :

Solution

La première équation comporte des logarithmes décimaux (logarithmes de base 10).

On doit d’abord exclure les réels x pour lesquels l’équation n’a pas de sens.

Il faut que :

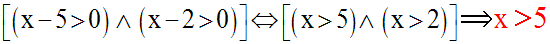
Résolution de l’équation

On a :

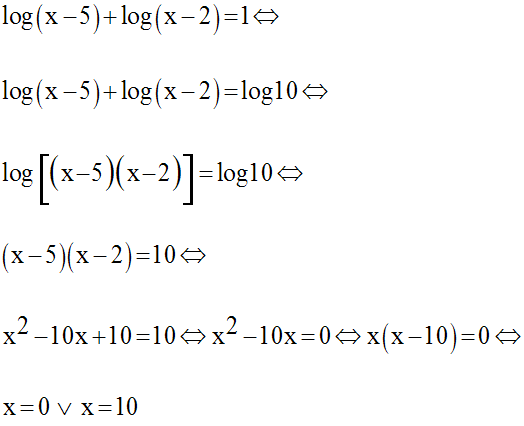
Comme x devra être strictement supérieur à 5, la valeur 0 devra être rejetée.

L’équation donnée admet donc une seule racine réelle égale à 10.

Les conditions portant sur la seconde équation sont :

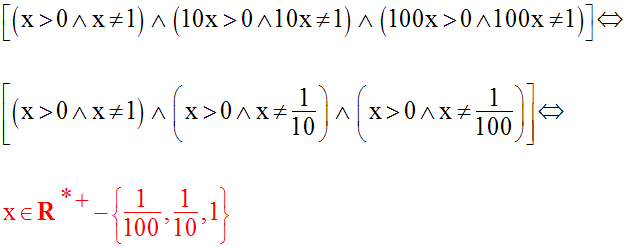
Pour la résoudre, il faut savoir que :

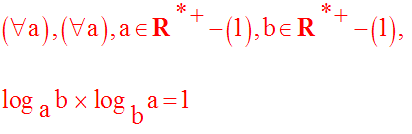
Démonstration

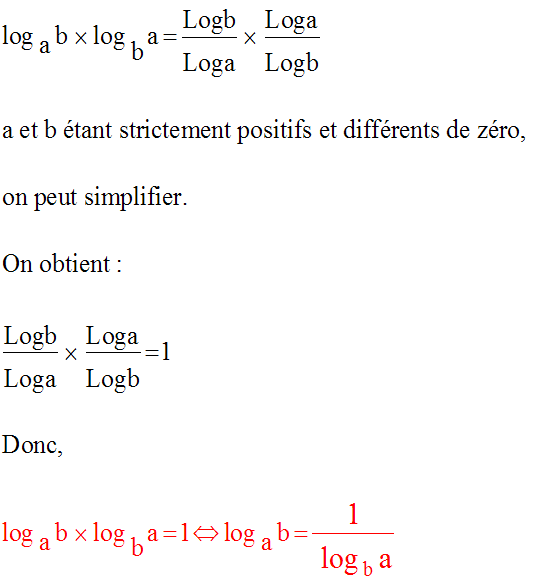
On applique cette formule à chacun des termes du premier membre de l’équation ;
on obtient :

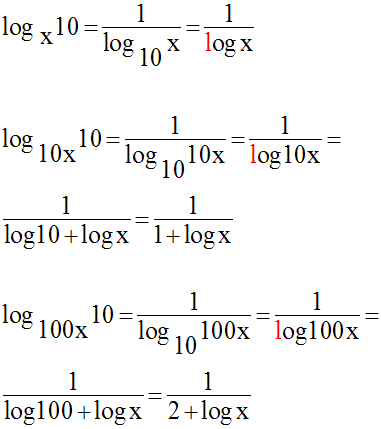
La seconde équation est donc logiquement équivalente à :

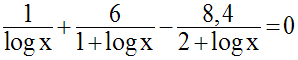
On pose logx = X ; l’équation s’écrit alors :

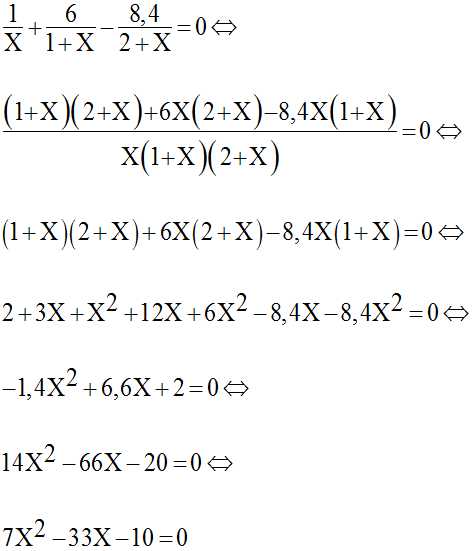
On obtient ainsi une équation du second degré en X.

Son discriminant est :

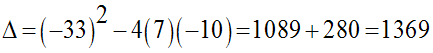
Les racines sont donc :

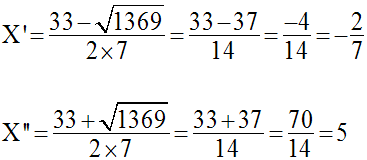
Revenant à logx, on obtient :

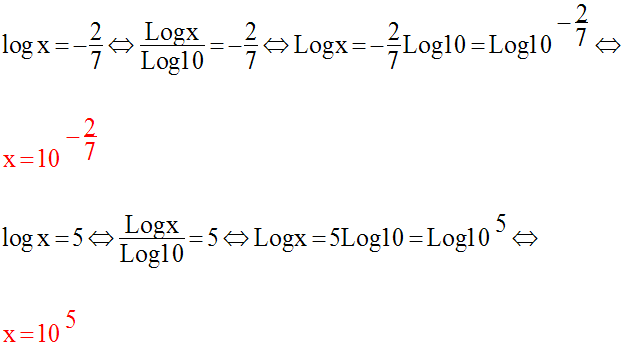
Les deux valeurs trouvées répondent aux conditions posées, donc elles sont acceptables.

2)

Résous dans R les équations suivantes :
 

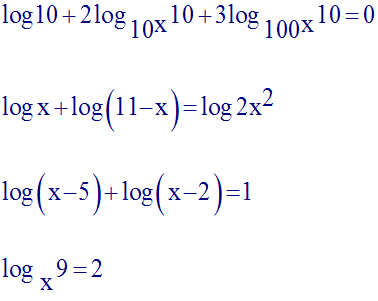
Solution

Pour la première équation, on a :

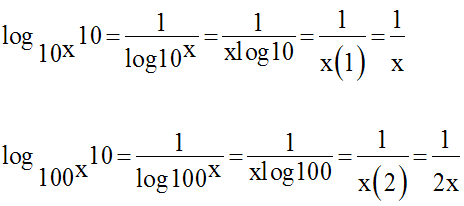
L’équation est donc logiquement équivalente à :

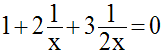
Il faut que x soit un réel différent de zéro.

On résout cette équation ; on a :

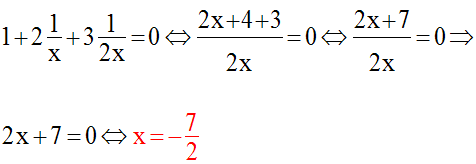
La seconde équation n’a de sens que si l’on a :

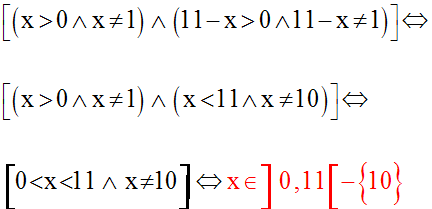
Cette condition posée, on la résout :

Je te laisse résoudre la troisième équation.

La quatrième équation est logiquement équivalente à :

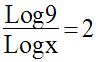
Elle n’a de sens que si x est strictement positif et différent de 1.

Cette condition étant posée, on la résout ; on a :

3)

Résous dans R² le système suivant :

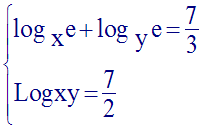
Solution

Le système n’a de sens que si :

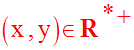
La condition sur x et y posée, on a :

En posant Logx = X et Logy = Y, on obtient le système logiquement équivalent :

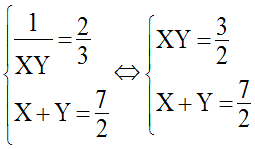
Les solutions de ce système sont celles de l’équation du second degré en X dont
la somme des racines et leur produit sont respectivement :

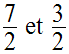
Donc, on résout l’équation suivante :

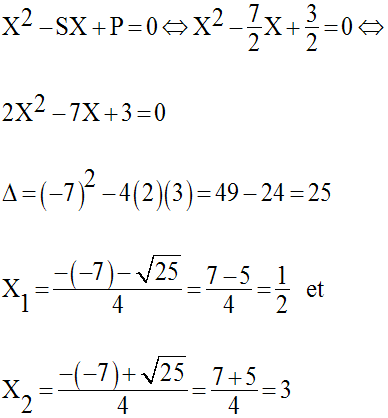
D’où le système :

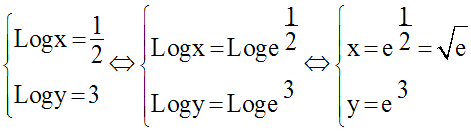
Comme x et y peuvent se permuter dans le système donné, ce dernier admet
donc deux solutions :

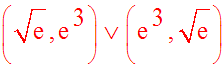
4)

a, b et c désignant trois réels strictement positifs et différents de 1, évalue :

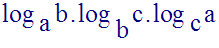
Solution

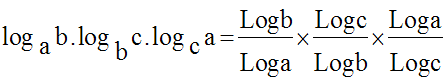
Comme a, b et c sont différents de 1, par conséquent leurs logarithmes
différents de zéro, on peut simplifier et on obtient :

5)

Dans le système de logarithmes décimaux (base 10), soit x un réel strictement
positif quelconque.

On appelle cologarithme de x et on écrit :

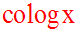
le logarithme décimal de l’inverse de x.

Ainsi, on a :

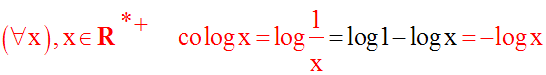
Résous dans R l’équation :

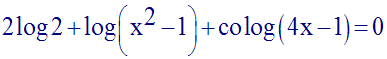
Solution

Le réel x devra d’abord vérifier le système de conditions :

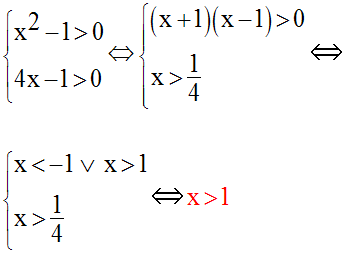
Cette condition posée, on résout l’équation ; on a :

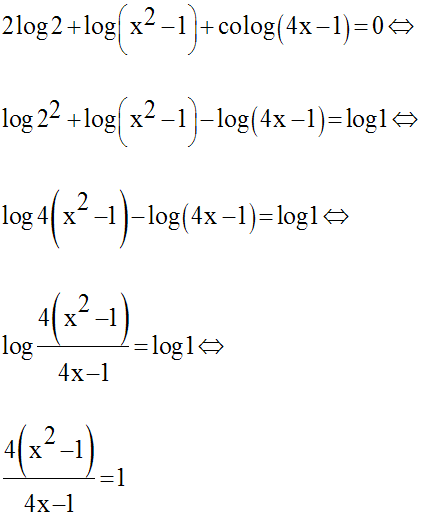
Comme x est strictement supérieur à 1, le dénominateur du premier membre
de cette dernière équation est différent de zéro ; donc on peut écrire :

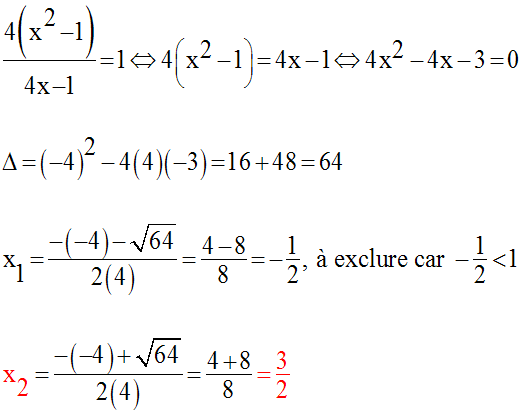
L’équation donnée admet dans R une seule racine égale à 1,5.

6)

Résous dans R l’équation :

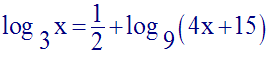
Je te laisse la résoudre ; elle mène vesr la résolution d’une équation du
second degré en x.

Tu trouveras deux racines dont une est à exclure car elle ne vérifie pas
la condition que doit vérifier x.

L’autre sera la solution de l’équation donnée et est égale à 15.

7)

Résous dans R l’inéquation :

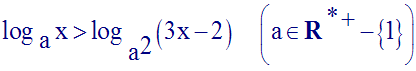
Solution

x devra d’abord vérifier la condition :

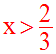
Par ailleurs, on a :

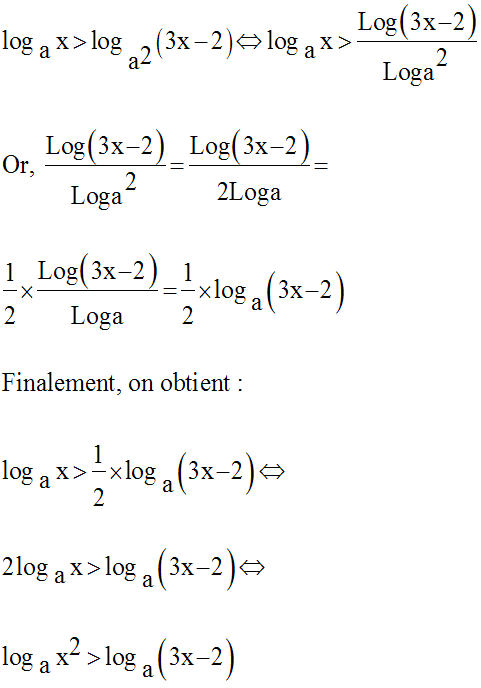
Deux cas sont à envisager :

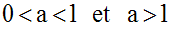
1^er cas : 0 < a < 1

La fonction log_a est alors strictement décroissante sur son domaine R^{* +}.

Par conséquent, on a :

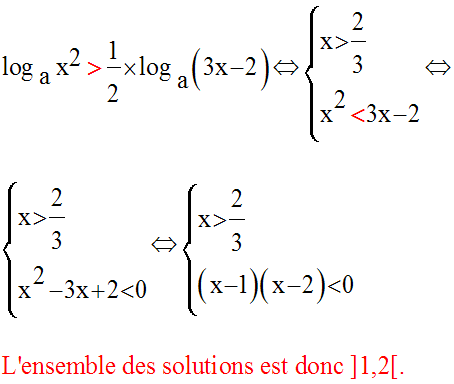
2^ème cas : a > 1

La fonction log_a est alors strictement croissante sur son domaine R^{* +}.

Par conséquent, on a :

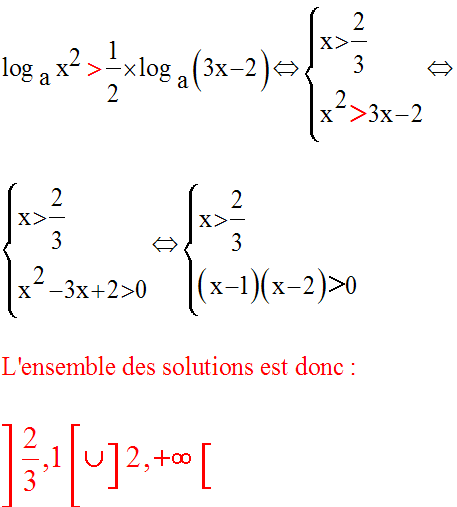
8)

Résous dans R l’inéquation :

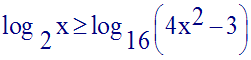
Solution

x devra d’abord vérifier la condition :

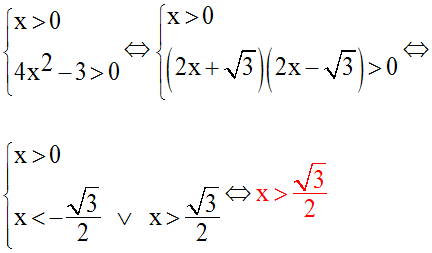
Par ailleurs on a :

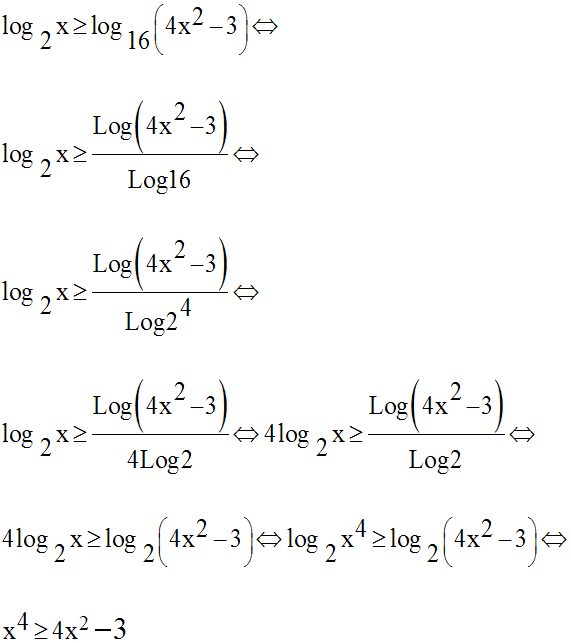
Ainsi, on a à résoudre le système :

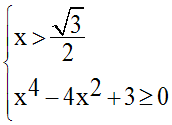
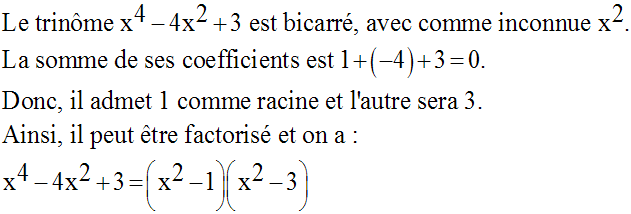
Notre système est donc équivalent à :

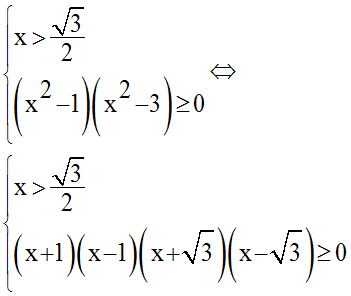
Le tableau des signes de la seconde inéquation donne :

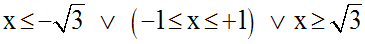
La représentation des conditions sur un axe orienté donne :

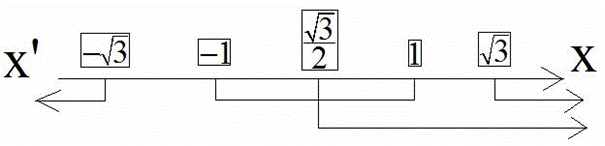
Elle montre que l’inéquation donnée admet comme ensemble de solutions :

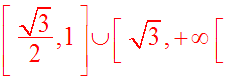
9)

Démontre que, pour tout réel x strictement positif et différent de 1, on a :

Solution

Pour chaque terme de cette somme, on applique la relation :

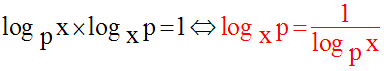
Ainsi, on a :

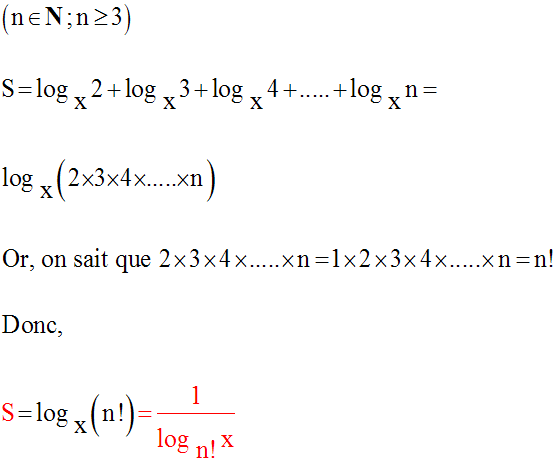
10)

Résous dans R l’équation :

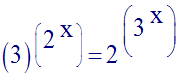
On utilisera les logarithmes décimaux

Solution

On a :

11)

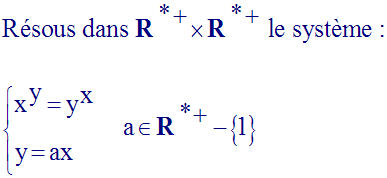
Solution

Compte tenu de la seconde équation, la première s’écrit :

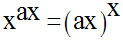
En prenant les logarithmes népériens des deux membres, on obtient :

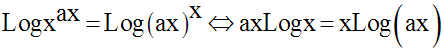
Comme x est strictement positif, on peut simplifier ; on obtient :

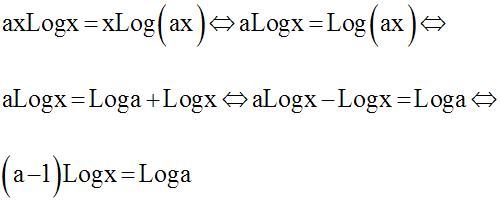
Comme a est différent de 1, on peut écrire :

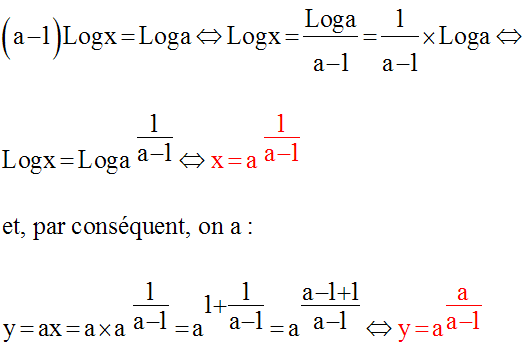
12)

Résous dans R l’équation :

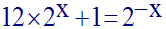
Solution

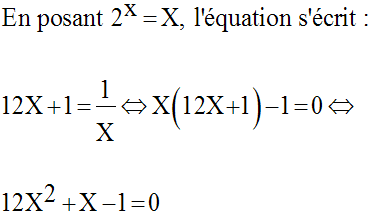
On obtient ainsi une équation du second degré en X.

Son discriminant est :

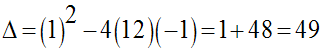
Ses racines sont donc :

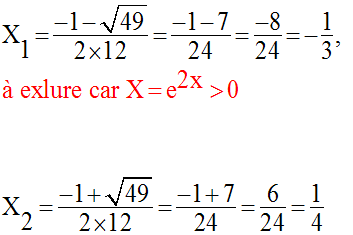
Ainsi, on obtient :

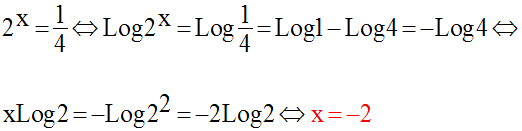
13)

Résous dans R l’équation :

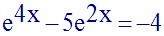
Solution

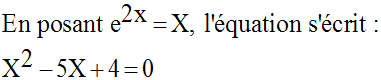
On reconnaît une équation du second degré en X et dont la somme des
coefficients est nulle.

Donc, une de ses racines est 1 et l’autre est 4.

On obtient ainsi :

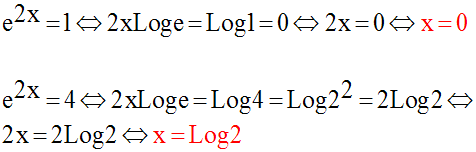
14)

On donne la fonction numérique f définie comme suit :

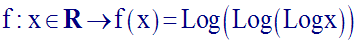
Trouve son domaine de définition.

Solution

Logx n’est pas définie pour x réel largement négatif.

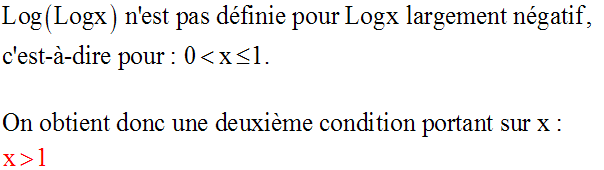
Finalement, on obtient :

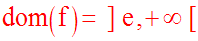
15)

Détermine la limite, quand x tend vers 0, de la fonction numérique f
définie comme suit :

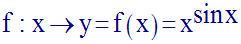
Solution

On doit d’abord trouver le domaine de définition, dom(f), de f.

On a la suite d’équivalences logiques suivantes :

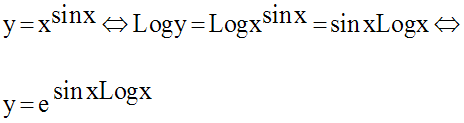
La dernière expression de y montre donc que x doit être strictement positif
car Logx n’est pas définie pour x largement négatif.

Ainsi, on obtient :

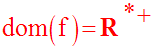
Pour x égal à 0, la fonction prend la forme indéterminée :

Levons cette indétermination par passage aux logarithmes népériens ;
on obtient :

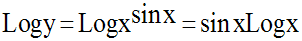
Comme x est différent de 0, on peut écrire :

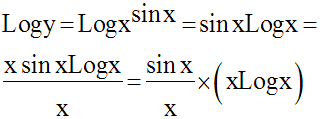
Or, on sait que :

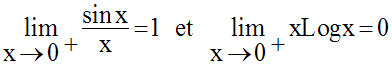
Donc, on obtient :

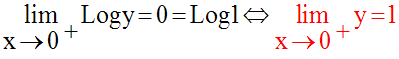
16)

Solution

On doit d’abord trouver le domaine de définition, dom(g), de g.

On a la suite d’équivalences logiques suivantes :

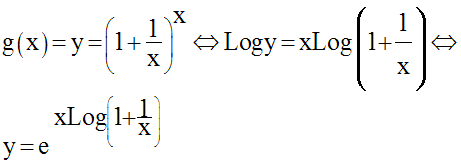
Ainsi,

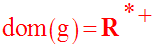
On a :

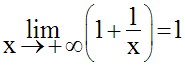
Donc y se présente sous la forme indéterminée :

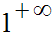
Levons cette indétermination par passage aux logarithmes népériens ;
on obtient :

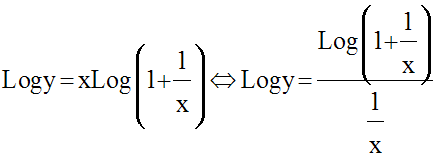
On sait que :

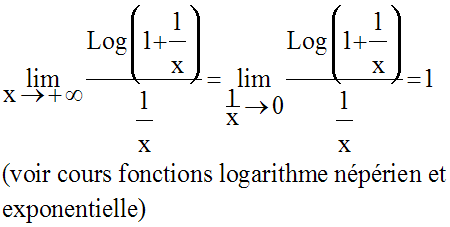
Donc,

17)

Solution

Par passage aux logarithmes népériens, on obtient :

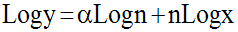
Or, n tendant vers l’infini, est différent de 0 ; on peut donc écrire :

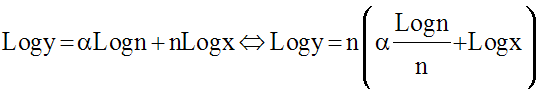
On sait que :

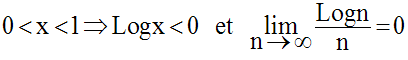
Il en résulte que :

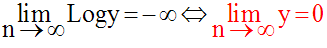
18)

Trouve les limites suivantes :

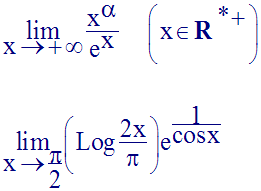
Je te laisse trouver la première limite ; la réponse est :

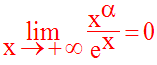
Solution pour la seconde limite

Deux cas sont à envisager :

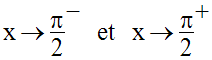
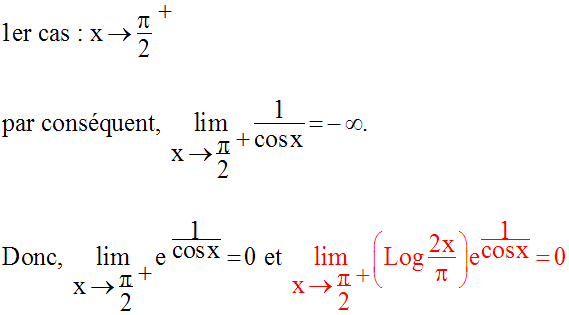
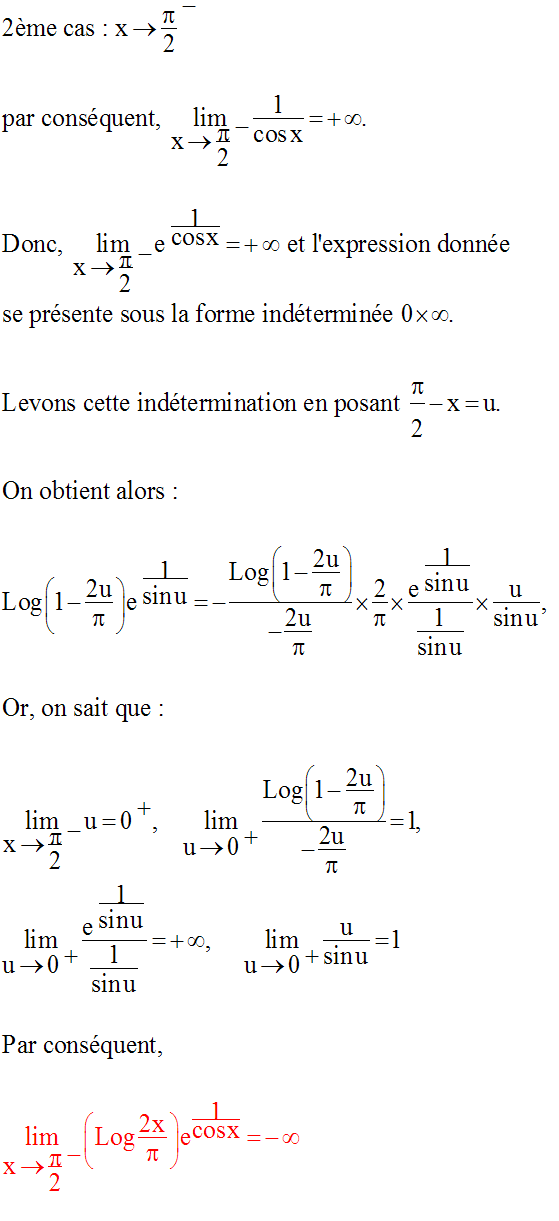
19)

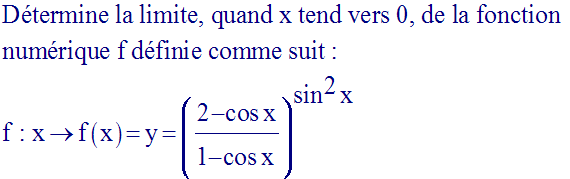
Solution

On a :

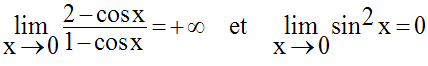
y se présente donc sous la forme indéterminée :

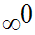
Levons cette indétermination par passage aux logarithmes népériens ;
on écrit :

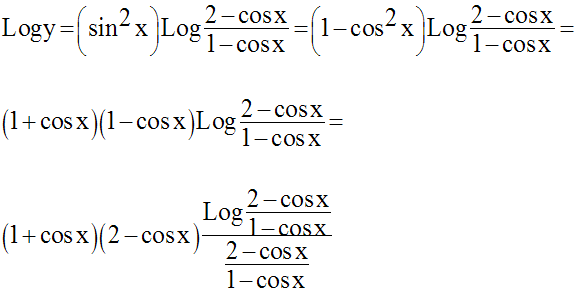
Or, on sait que :

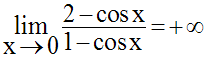
Donc,

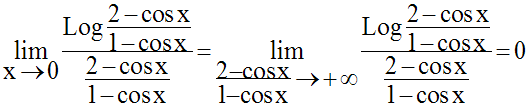
Par ailleurs, on a :

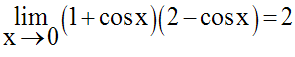
Donc, finalement :

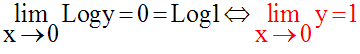
20)

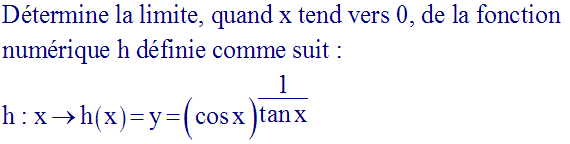
Solution

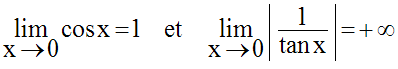
y se présente donc sous la forme indéterminée :

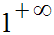
Levons cette indétermination par passage aux logarithmes népériens ;
on écrit :

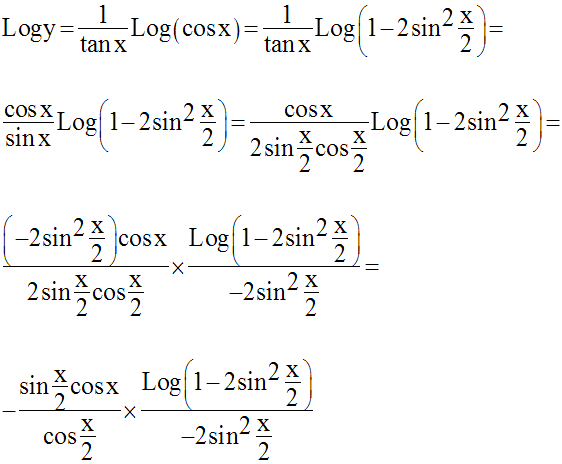
Or, on sait que :

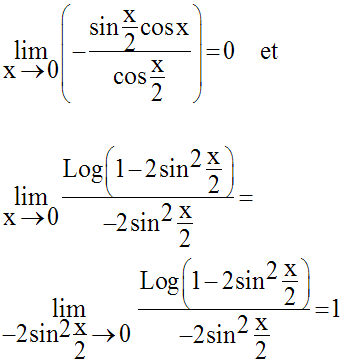
Donc, finalement :

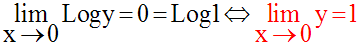
21)

a désignant une constante réelle, on considère les applications f_a de l’ensemble
des réels dans lui-même, définies par :

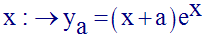
1°

Calcule la fonction dérivée de f_a. En déduis les dérivées successives et les
primitives de cette fonction.

2°

Etudie et représente graphiquement, dans un repère orthonormal, la fonction
f₀ définie par :

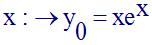
Montre que la courbe représentative (C₀) admet un point d’inflexion et écris
l’équation de la tangente d’inflexion.
Calcule l’aire géométrique A du domaine fermé limité par (C₀), sa tangente
d’inflexion et l’axe des abscisses.

3°

On désigne par (C_a) le graphe de f_a dans un repère donné.
Détermine si a décrit R,

-        l’ensemble (E₁) des points des courbes (C_a) où la tangente est parallèle
à l’axe des abscisses ;

-        l’ensemble (E₂) des points d’inflexion des courbes (C_a).

Solution

1°

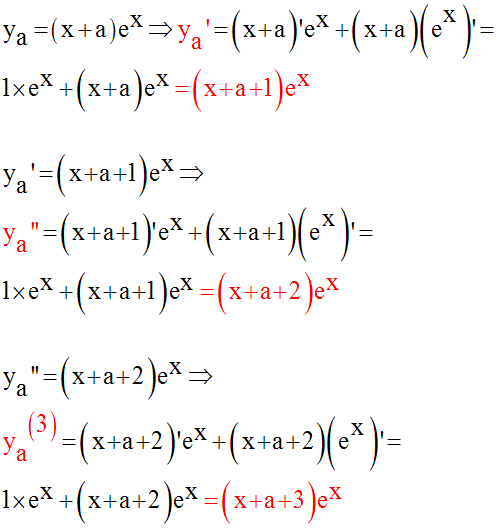
Supposons que cette relation est vraie pour le rang (n – 1) ;
nous avons donc :

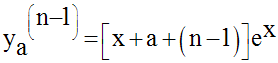
Démontrons qu’elle est vraie pour le rang n.

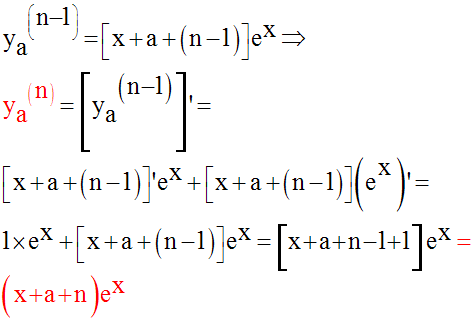
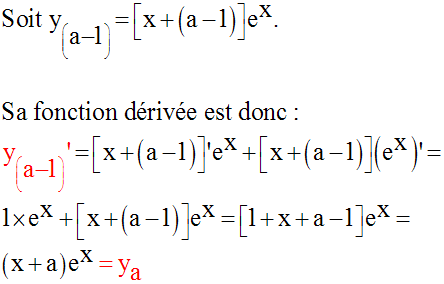
Ainsi, nous avons :

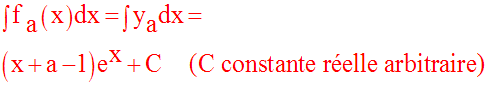
2°

Elle est dérivable sur R.

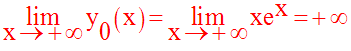
Par ailleurs, nous avons :

Calculons les deux premières dérivées de f₀.

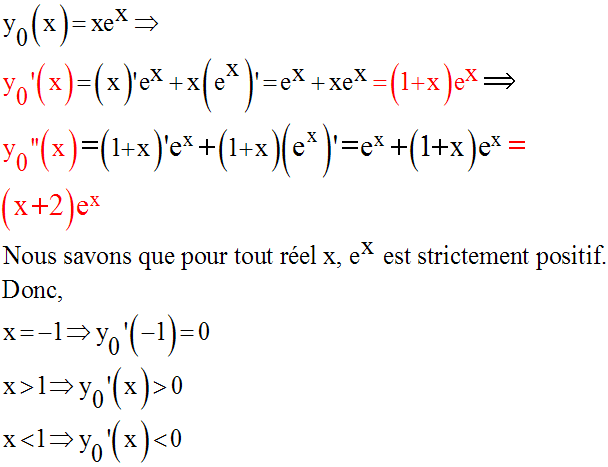
Comme elle est également continue sur R, elle admet donc dans R un
minimum absolu égal à :

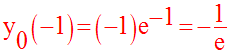
Par ailleurs,

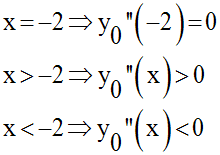
La dérivée seconde s’annulant au point noté I de (C₀) d’abscisse – 2
en changeant de signe, ce point est un point d’inflexion pour (C₀).

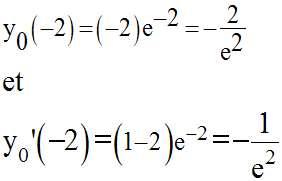
La droite passant par I et tangente à (C₀) a donc pour équation :

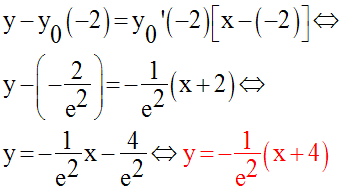
Les variations de f₀ sont résumées dans le tableau suivant :

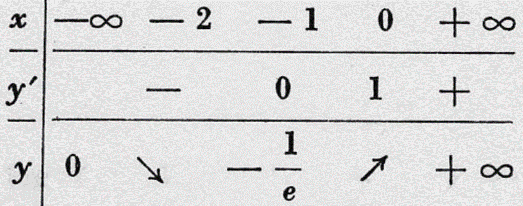
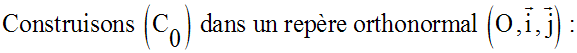
La tangente, en I, à (C₀) rencontre l’axe des abscisse au point M d’abscisse
x_M et d’ordonnée 0.

Donc,

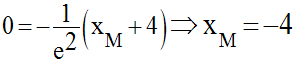
Le domaine fermé est donc (MIOM), la portion (IO) appartenant à (C₀).

Son aire géométrique est la somme des aires suivantes :

-        Aire géométrique du triangle rectangle (MIi), i étant le projeté orthogonal
de I sur l’axe des abscisse

-        Aire géométrique du domaine (IOiI)

L’aire géométrique du triangle (MIi) est égale à :

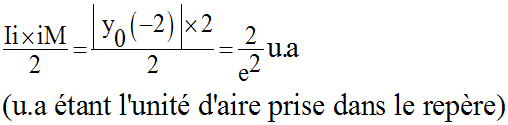
L’aire géométrique du domaine (IOiI) est égale à :

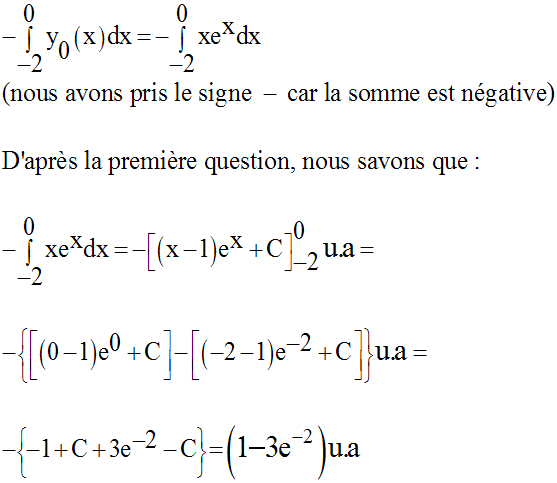
Par conséquent,

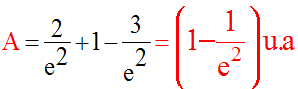
3°

Nous avons :

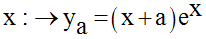
Toute tangente à (C_a) au point M(x , y) appartenant à  (C_a) a pour
coefficient directeur (ou pente) :

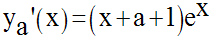
Pour que cette tangente soit parallèle à l’axe des abscisses,
il faut et il suffit que :

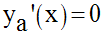
(E₁) est donc l’ensemble des points M(x , y) tels que :

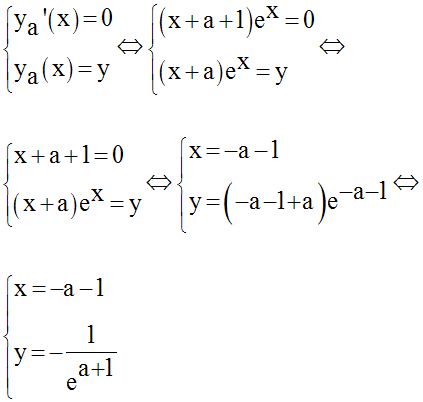
En éliminant a, nous trouvons l’équation de (E₁) :

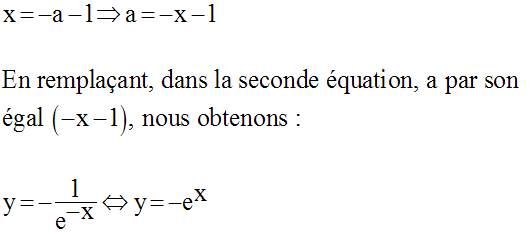
L’équation de (E₁) est donc :

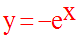
(E₂) est l’ensemble des points d’inflexion I(x , y) ; donc les cordonnées
de I doivent vérifier le système :

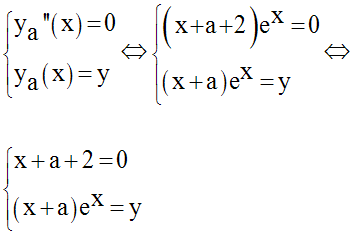
En éliminant a, nous trouvons l’équation de (E₂) :

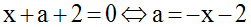
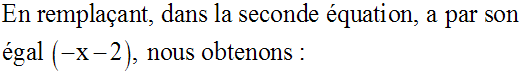
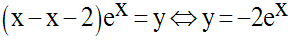
L’équation de (E₂) est donc :

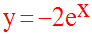
22)

1°

Etudie les variations de la fonction numérique définie comme suit :

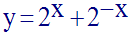
On nomme (C) son graphe dans un repère orthonormal.

2°

Soit (D) le domaine limité par l’axe des abscisses, l’axe des ordonnées,
(C) et la droite d’équation :

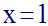
Construis (C) et calcule l’aire, S, du domaine (D).

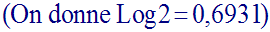
Solution

Elle est dérivable sur R.

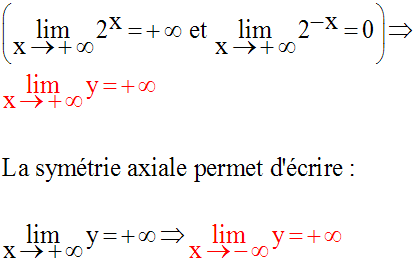
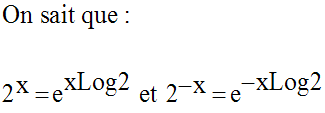
La fonction dérivée est donc :

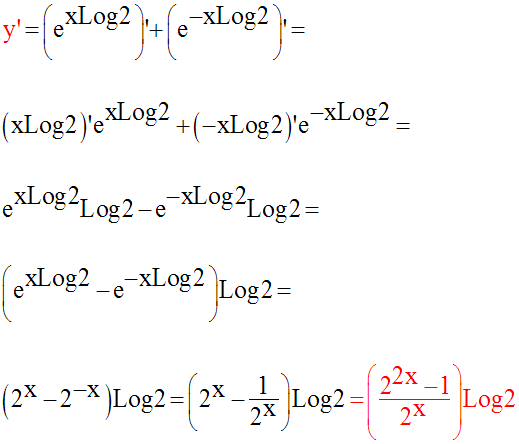
Pour x nulle, y est égale à 2.

Enfin, comme on a :

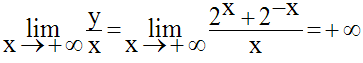
y admet une branche parabolique dans la direction des ordonnées positives.

Les variations de y sur R⁺ sont résumées dans le tableau suivant :

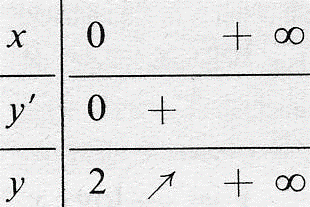
La symétrie axiale permet de compléter l’étude en écrivant :

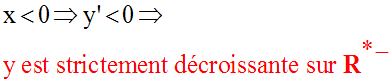
y admet une branche parabolique dans la direction des ordonnées positives.

y étant continue sur R, strictement décroissante sur R^{* –}, strictement
croissante sur R^{* +}, égale à 2 pour la valeur de x annulant sa dérivée, admet
un minimum absolu égal à 2.

2°

On construit le graphe (C) de y dans un repère orthonormal et on
hachure le domaine (D) pour lequel on doit calculer l’aire S.

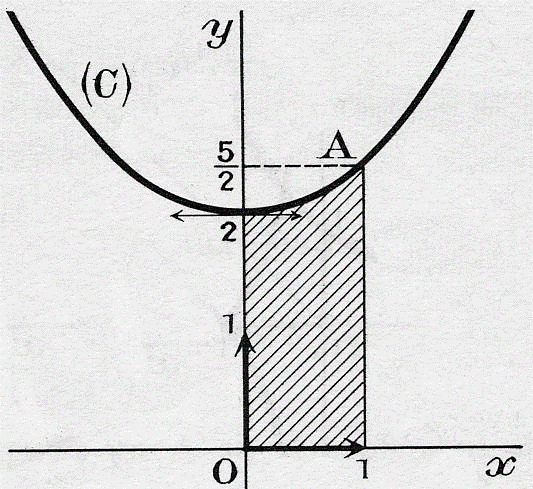
Ainsi, on a :

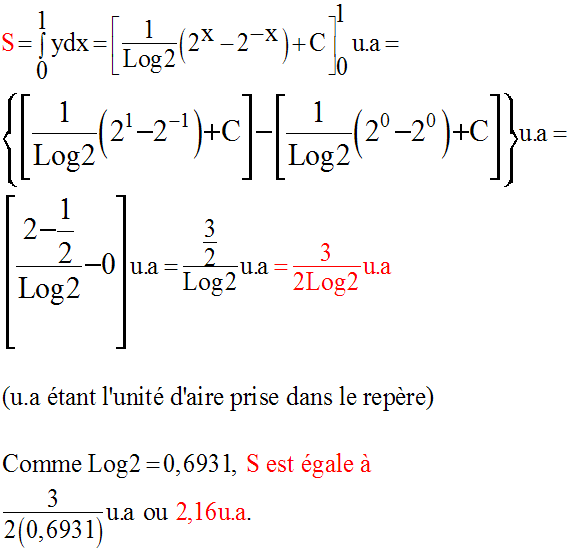
23)

Le plan orienté étant rapporté à un repère orthonormal direct (Ox , Oy), on
considère les courbes (C₁) et (C₂) représentant graphiquement les deux
fonctions numériques :

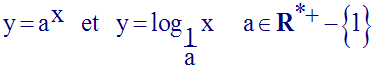
Sans étudier ces fonctions numériques et sans construire leurs courbes
représentatives, trouve la transformation géométrique simple qui transforme
(C₁) en (C₂).

Trouve la relation indépendante de a qui existe entre les coordonnées du
point commun à (C₁) et à (C₂).

Solution

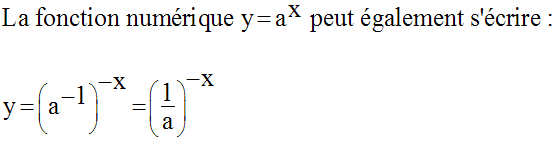
Le passage aux logarithmes népériens donne :

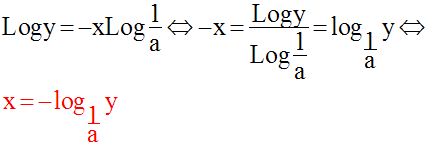
C’est l’équation de la fonction réciproque de la fonction numérique :

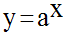
On sait que le graphe (C’) de cette fonction réciproque est symétrique de
(C₁) par rapport à la première bissectrice.

Si on représente (C’) dans le même repère que celui de (C₁), on prendra
alors, pour équation de (C’) l’équation :

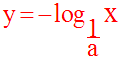
Cette équation montre que (C’) est symétrique de (C₂) dans la symétrie
axiale d’axe (x’Ox).

Ainsi, on passe de (C₁) à (C₂) par le produit de deux symétries axiales :

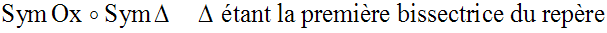
Or, on sait que le produit de deux symétries axiales dont les axes sont concourants
est égal à une rotation de centre, le point d’intersection des axes et d’angle,
l’angle que forment ces deux axes.

Par conséquent, on obtient :

Finalement, on passe de (C₁) à (C₂) par la rotation de centre O, l’origine du
repère, et d’angle de rotation dont la mesure est – 90°.

On sait que les coordonnées d’un point commun à (C₁) et (C₂)
vérifient le système :

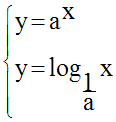
Le passage aux logarithmes népériens donne :

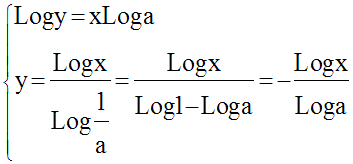
L’élimination de Loga, différent de zéro, entre les deux équations
du système donne :

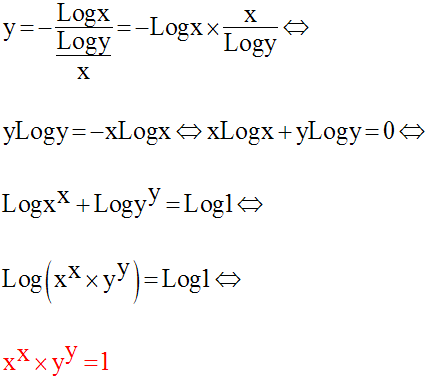
Cette relation montre que l’ensemble des points communs à (C₁) et (C₂)
appartient au premier quadrant du repère et admet comme axe de symétrie,
la première bissectrice.

24)

Dans un repère orhonormal, on donne deux courbes (C) et (P) d’équations
respectives :

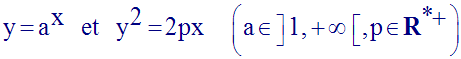
1°

Trouve la relation (R) à laquelle doivent satisfaire a et p pour que les courbes
(C) et (P) soient tangentes.

2°

Les réels a et p variant de telle manière que la relation (R) soit satisfaite,
détermine l’ensemble des positions du point de contact, A, de ces
deux courbes.

3°

Démontre que le point, S, où la tangente commune en A aux deux courbes
coupe l’axe des ordonnées, reste fixe lorsque a et p varient comme il est
dit ci-dessus.

Je te laisse résoudre cet exercice avec les recommandations suivantes :

1°

Il faudra poser un système d’équations exprimant qu’au point commun aux
deux courbes, les coordonnées de ce point vérifient leurs équations respectives
et les valeurs prises par les dérivées respectives sont égales.

Le système que tu trouveras et qui te permettra de trouver (R) est :

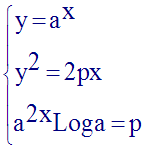
La relation (R) est :

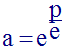
2°

(R) étant satisfaite, les coordonnées de A sont :

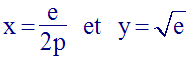
L’ensemble des points A est toute la demi-droite ]Bu) située dans le demi-plan
des abscisses positives, B étant l’intersection de la droite issue de A et parallèle
à l’axe des abscisses.

3°

Tu dois trouver l’équation de la droite tangente commune aux deux courbes,
en A, puis ensuite les coordonnées de son intersection, S,  avec l’axe des
ordonnées.

Tu trouveras :

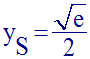
Cette ordonnée étant un réel constant, S est donc fixe.

retour au sommaire