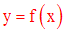
LA FONCTION NUMERIQUE - GENERALITES

 

 

 

1- Définitions

Soient E et F deux ensembles quelconques.

Une relation f de E vers F est dite fonction de E dans F si et seulement si tout élément appartenant à E possède par f au plus une image appartenant à F.

E et F seront respectivement nommés source et but de f.

x étant un élément de la source E et possédant par f une image y élément du but F, on écrira :

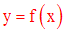
qui se lit « y est égale à l’image de x par f ».

On dira également que y possède par f un antécédent égal à x et appartenant à la source E.

Donc, il peut exister dans E des éléments n’ayant pas d’image par f.

L’ensemble des éléments de E possédant une image par f dans F est nommé domaine de définition de f et se note : dom(f).

L’ensemble des éléments de F possédant des antécédents par f dans E est nommé image de E par f et se note : Im(f) ou f(E).

D’après ces définitions, si f est une fonction de E dans F alors f est une application de dom(f) dans F.

Exemple :

 

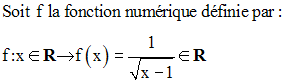
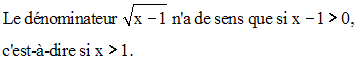
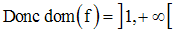
Remarque

Lorsqu’on nous demande d’étudier une fonction numérique, il faut toujours commencer par trouver son domaine de définition.

Exercice

Trouve le domaine de définition de chacune des fonctions numériques qui suivent :

 

 

 

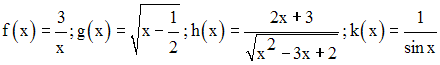
Composée de deux fonctions

On donne deux fonctions f et g définies respectivement par leurs données :

(E, F, Gf ) et (F, G, Gg )

On a donc f une fonction de E dans F et g une fonction de F dans G.

Soient Dom(f), le domaine de définition de f et Dom(g) celui de g.

On sait que :

Soit Im(f) l’ensemble des éléments de F possédant des antécédents dans E.

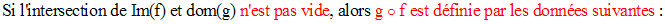
Sa source est E

Son but est G

Son domaine de définition est défini comme suit :

 

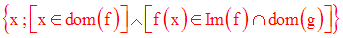
Exemples

 

1-

On donne deux fonctions f et g définies comme suit :
 


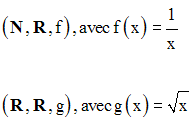
On a :

dom(f) = N*  et  dom(g) = R+  

Im(f) est donc égal à Q* +.


Par conséquent, on a :



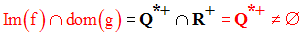
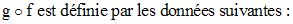
Sa source est N

Son but est R

Son domaine de définition défini comme suit :



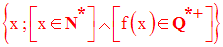
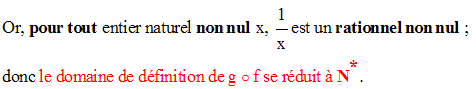
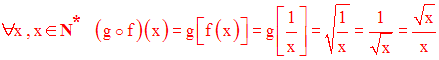
2-

On donne deux fonctions h et i définies comme suit :
 

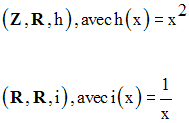
On a :

dom(h) = Z  et  dom(i) = R*  

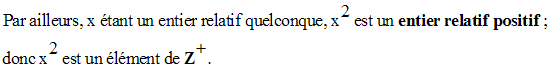
Im(h) est donc égal à Z+.

Par conséquent, on a :

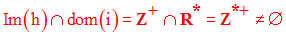
(i o h) est définie par les données suivantes :

Sa source est Z

Son but est R

Son domaine de définition défini comme suit :


 

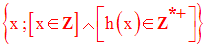
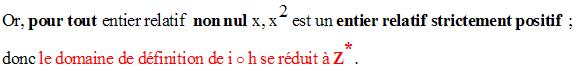
3-

On donne deux fonctions numériques f et g définies comme suit :

f(x) = 6x – 4

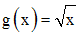
On a :

dom(f) = R  et  dom(g) = R+  

Par ailleurs, on a :

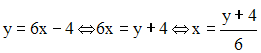
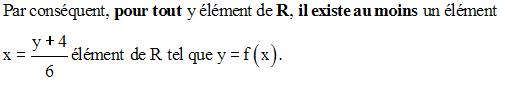
f est donc surjective et on a Im(f) = R.

Par conséquent, on a :

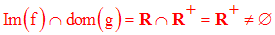
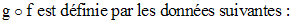
Sa source est R

Son but est R

Son domaine de définition défini comme suit :

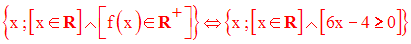
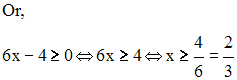
Par conséquent,

 

 

 

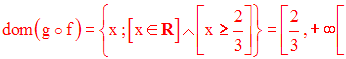
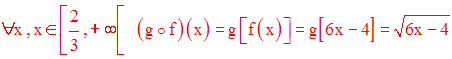
Dans tout ce qui suit, on supposera E = F = R et R muni de la distance d définie par :

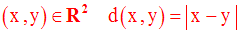
L’ensemble des intervalles ouverts de R qui découle de ces hypothèses est une topologie de R associée à d.

Dans ces conditions, f est dite fonction numérique ou fonction réelle d’une variable réelle.

 




 

2- Limites et continuité

Soient I un intervalle de R et f une fonction numérique de I dans R.

Soit un élément réel a tel que :

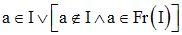
Soit A la partie de R définie comme suit :

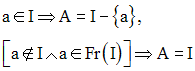
Tout voisinage Va de a rencontre A ; donc a est adhérent à A et on a :

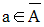
On écrira :

 

 

On dira que f(x) a une limite k quand x appartenant à A tend vers a si, pour tout voisinage Vk de k dans R, il existe un voisinage Va de a dans R tel que :

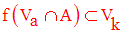
On note donc :

 

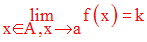
Cette écriture est logiquement équivalente à la suivante :

 

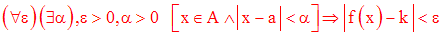
Exercice

Démontre la propriété suivante :

Si la limite existe, alors elle est unique.

Extension de la notion de limite

Soit A un réel strictement positif quelconque.
 








 


 

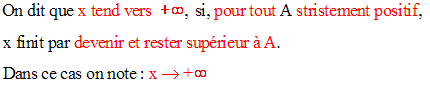
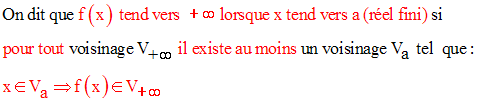
Cette définition est logiquement équivalente à la suivante :


 

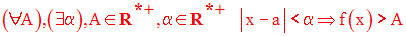
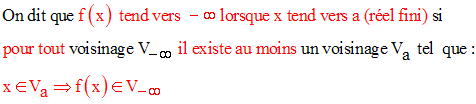
Cette définition est logiquement équivalente à la suivante :


 

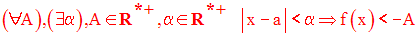
Cette définition est logiquement équivalente à la suivante :

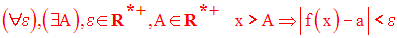
ou


 

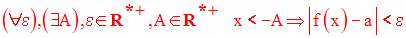
On pourra définir de la même manière l’expression suivante :

en prêtant attention aux différents signes que peut prendre l’infini.

 

Opérations sur les limites

 

Soient les fonctions numériques f i avec i = 0, 1, 2, 3, …, n entier naturel.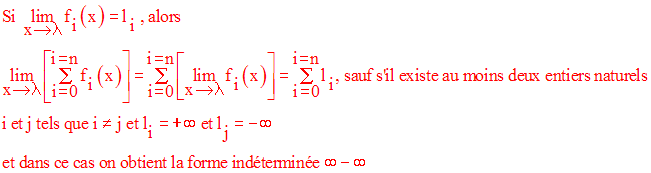



 

 

Soient des réels A i avec i = 0, 1, 2, …, n entier naturel.

Leur produit A0 . A1 . A2 . A3 ….. An se note :





 

 

 

 

 

 

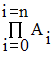
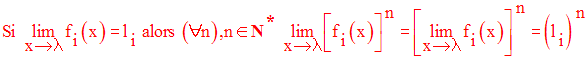
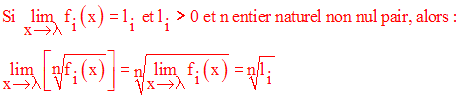
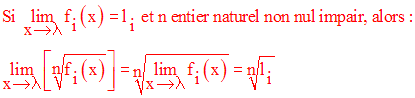
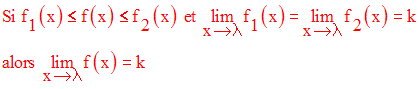
Chacune des assertions qui précèdent immédiatement est facilement démontrable, en utilisant la définition de la limite d’une fonction en un point réel.

 

Notons enfin l’importance de la dernière assertion qui est souvent utilisée dans des exercices ou problèmes.

Exemples :

 

 

 

 

 

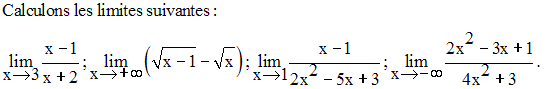
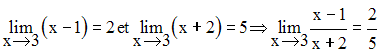
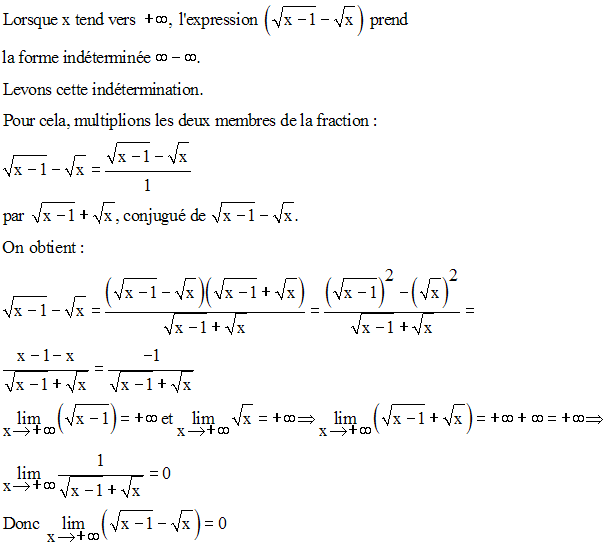
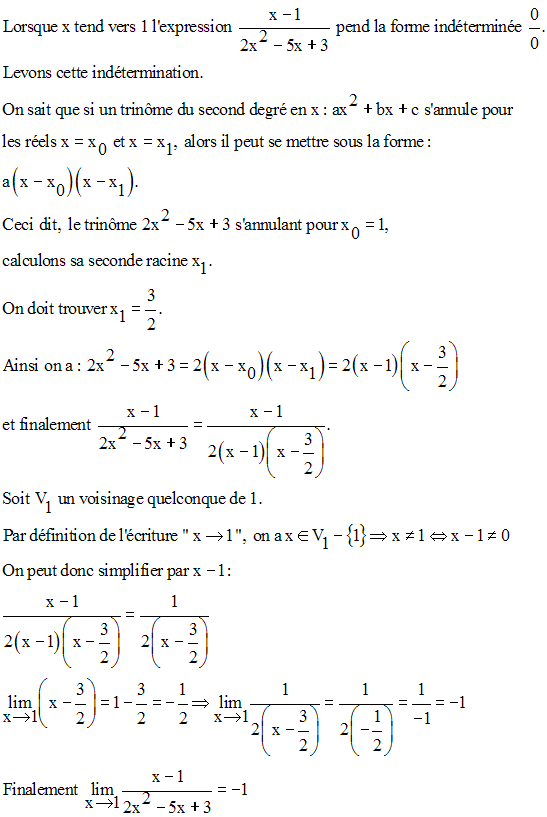
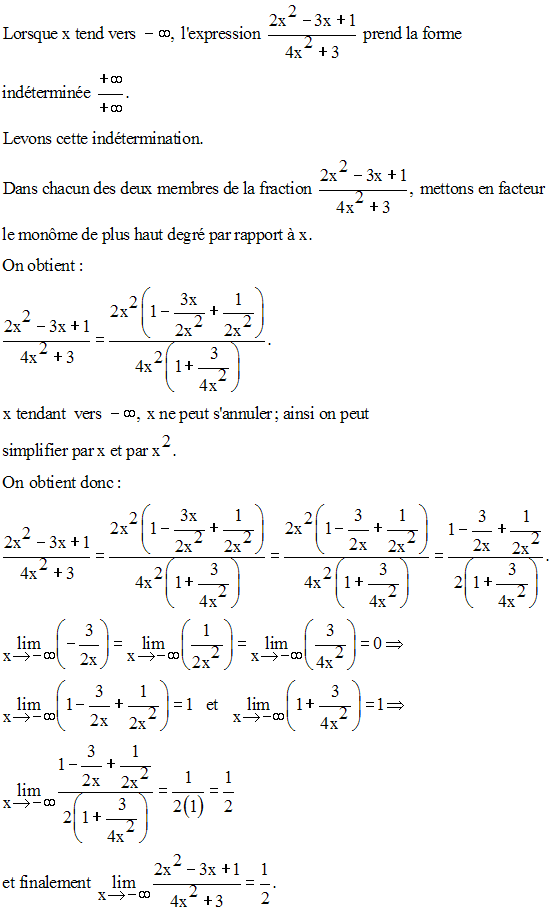
Exercices

1)

Montre l’assertion suivante :

 

Soient les fonctions numériques f i avec i = 0, 1, 2, 3, …, n entier naturel.

 

 

2)

Trouve les limites suivantes :

 

 

 

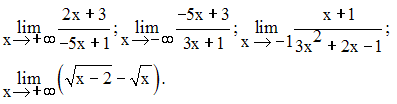
Limite à gauche et limite à droite ; continuité à gauche et continuité à droite

Soit I un intervalle ouvert de R et J un intervalle quelconque inclus dans I.

Fr(J) est un ensemble pair dont les éléments sont les deux extrémités de J, à gauche et à droite.

Posons Frg (J) l’extrémité à gauche et Frd (J) celle de droite.

Soit a un élément appartenant à R.

Si l’on a :

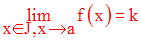
alors on dira que f(x) tend vers k quand x élément de I tend vers a à droite.

On note dans ce cas :

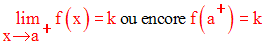
Cette définition est logiquement équivalente à :

 

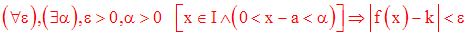
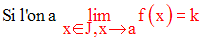
alors on dira que f(x) tend vers k quand x élément de I tend vers a à gauche.

On note dans ce cas :

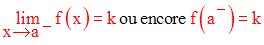
Cette définition est logiquement équivalente à :

 

 


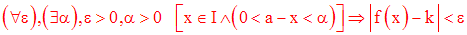
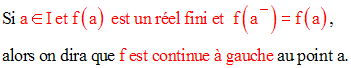
Continuité

 

Exemples :

1)

 

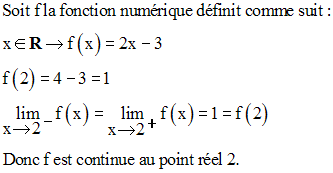
2)

 

3)

Soit la fonction numérique, notée E(x), qui à tout réel x applique le plus grand entier relatif largement inférieur à x.

Par exemple :

 

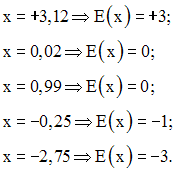
E(x) est appelé fonction en escalier du fait que sa courbe représentative dans un repère quelconque ressemble à un escalier.

Etudions la continuité de E(x) au point 0.

E(0) existe et est finie ; elle est égale à 0.

 

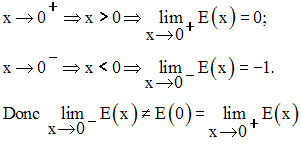
Conclusion :

La fonction E(x) est continue à droite au point 0. Elle n’est pas continue au point 0, puisque la continuité à gauche en ce point n’est pas vérifiée.

On pourra vérifier que cette fonction n’est continue en aucun point x élément de Z.


Exercices

1)

 


2)

 

 

Remarques

1)

Pour montrer que f est continue au point a il suffit de montrer que :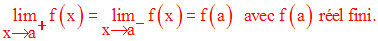

 

2)

f n’est pas continue au point réel fini a si une au moins des conditions suivantes est vérifiée :

f n’est pas définie au point a ; c’est-à-dire a n’appartient pas à dom(f) ;

 

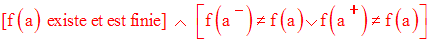
3)

 

Exemple :

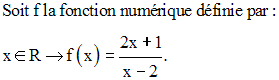
Le dénominateur ne peut être nul ; donc dom (f) = R – {2}.

 

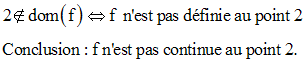
Etudions la limite de f au point 2.

 

De la même manière on pourra établir que :

 

 

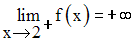
Prolongement par continuité d’une fonction numérique

Soit f une fonction numérique définie partout dans un intervalle réel I sauf au point a.

 

Exemple :

Soit f la fonction numérique définie comme suit :

 

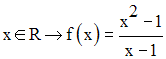
Le dénominateur ne pouvant être nul, x ne peut donc être égale à 1 et

dom (f) = R – {1}.

f n’étant pas définie au point 1, elle n’est pas continue en ce point.

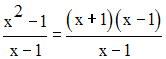
Comme x est différent de 1, (x – 1) est différent de 0 et on peut simplifier

par (x – 1) ; on obtient :

 

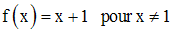
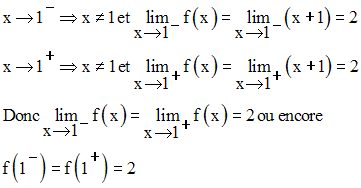
On peut donc prolonger f par continuité au point 1.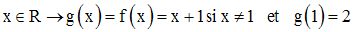

Il suffit de considérer la fonction numérique g définie dans R comme suit :

Ainsi on a bien :

 

 

Continuité sur un intervalle

f est dite continue sur un intervalle ouvert ]a , b[ de R si et seulement si f est continue
en tout point de ]a , b[.

f est dite continue sur un intervalle fermé [a , b] de R si et seulement si :

f est continue en tout point de ]a , b[,

f est continue à droite au point a,

f est continue à gauche au point b.

 

Opérations sur les fonctions continues sur le même intervalle



Soient f ; g deux fonctions continues sur un même intervalle I de R.

f + g et f . g sont également continues sur I.



 

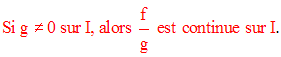
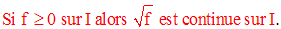
Soit h une fonction numérique continue sur l’intervalle J tel que :

 

 

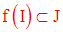
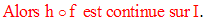
Théorèmes fondamentaux pour les fonctions numériques continues

Soit f une fonction numérique quelconque dont le domaine de définition est

dom (f).

On a vu que Im(f) est l’ensemble des réels possédant un antécédent dans

dom (f).



Si Im(f) possède dans R un plus petit majorant M, alors M est la borne supérieure de Im(f).

Par définition, M sera dite borne supérieure de f et sera notée :

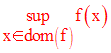
On dira dans ce cas que f est majorée sur son domaine de définition.

 

Si Im(f) possède dans R un plus grand minorant m, alors m est la borne inférieure de Im(f).

Par définition, m sera dite borne inférieure de f et sera notée :

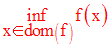
On dira dans ce cas que f est minorée sur son domaine de définition.



Si f est simultanément majorée et minorée sur son domaine de définition, alors on dira qu’elle est bornée sur son domaine de définition.

 

1)

Toute fonction numérique f continue sur un intervalle fermé I de R est bornée sur I.



2)

Soit f une fonction numérique continue sur un intervalle fermé I de R, donc bornée.

Les bornes inférieure et supérieure de f appartiennent à Im(f) = f (I) :

 

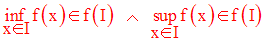
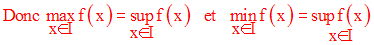
Démonstration

Il est évident que l’on a :

 

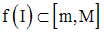
Montrons que m et M sont des éléments appartenant à f (I).

On fait uniquement la démonstration pour M, sachant qu’elle est la même pour m.

C’est une démonstration dite par l’absurde, c’est-à-dire on suppose que la propriété est fausse et
on démontre que cela mène à une contradiction avec les données de notre énoncé de départ.

 


Exercices

 

1)

Trouve les limites suivantes :


 

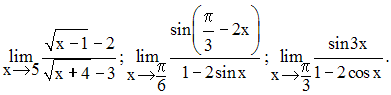
2)

Détermine les constantes réelles a et b pour que la fonction numérique f définie par :




 

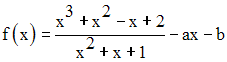
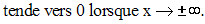
3)

On donne la fonction numérique f définie par :

Trouve son domaine de définition D et étudie la continuité de f sur D.
 

4)

On donne les fonctions numériques g et h définies par :

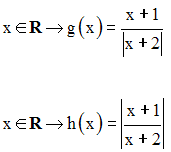
Trouve leurs domaines de définition et étudie leur continuité sur leurs domaines respectifs.

 

3- Fonctions monotones

Soit f une fonction numérique quelconque et soit I un intervalle quelconque de R.


 

f est dite croissante sur I si, quels que soient x, x’ de I



 

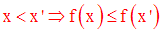
f est dite strictement croissante sur I si, quels que soient x, x’ de I



 

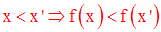
f est dite décroissante sur I si, quels que soient x, x’ de I

 

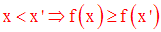
f est dite strictement décroissante sur I si, quels que soient x, x’ de I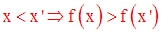



De ces définitions, on peut obtenir les conclusions suivantes :


 

Une fonction numérique croissante ou décroissante sur un intervalle réel, est dite monotone sur cet intervalle.

Elle est dite strictement monotone si elle est strictement croissante ou strictement décroissante.

 


Exercice

On donne la fonction numérique f définie par :

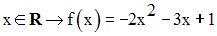
Etudie sa continuité sur son domaine de définition.

Montre qu’elle est strictement monotone sur chacun des intervalles :

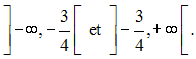
En déduis l’ensemble A des ses majorants et a = sup(f).

a appartient-elle à Im (f) ? Que peux-tu en conclure ?


Généralisation

On donne la fonction numérique f définie par :

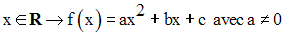
Montre qu’elle est continue sur R.

Selon le signe de a, étudie sa monotonie sur chacun des intervalles :

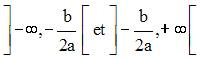
Que peux-tu conclure pour la quantité :

 

 

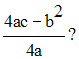
Monotonie et limites

Soit a un réel fini quelconque.

 


Monotonie et continuité

On admettra sans démonstration les théorèmes qui suivent.

Pour toute fonction f continue et strictement monotone sur un intervalle I de R, f -1 est une fonction dite réciproque de f,
continue, strictement monotone et de même monotonie que f, sur l’intervalle f (I).

De cette propriété découle la notion d’homéomorphisme en Topologie.


Définition

Une application f d’un intervalle réel I dans un intervalle réel J est appelée homéomorphisme si et seulement si :

f est une bijection de I sur J ;

f et l’application réciproque f -1 (qui est d’ailleurs une bijection de J sur I) sont toutes deux continues sur leurs intervalles
respectifs.

Alors f -1 est aussi un homéomorphisme.


Ainsi, f étant continue et strictement monotone sur un intervalle réel I, est bijective ; de plus, sa réciproque f -1 est
continue, strictement monotone et de même monotonie, sur f (I).
Par conséquent f et f -1 sont des homéomorphismes.

Si f est une fonction numérique continue et injective sur un intervalle I de R, alors f est strictement monotone sur I.

Donc f est un homéomorphisme de I sur f (I).


De cela découle que tout homéomorphisme d’un intervalle réel I sur un intervalle réel J est strictement monotone sur I.


Exercice

Soit la fonction numérique f définie par :

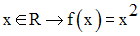
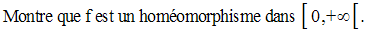
Trace la courbe C représentative de f dans un repère orthonormal.

Définis la réciproque f -1 de f et trace sa courbe C’ dans ce repère.

Montre que pour tout point M de C, sa symétrique M’ par rapport à (d), (d) la première bissectrice du repère,
appartient à C’ et que, pour tout point N de C’, sa symétrique N’ par rapport à (d) appartient à C.

C et C’ sont donc symétriques par rapport à (d).

Généralisation

Soit f un homéomorphisme d’un intervalle réel I sur un intervalle réel J.

Les courbes représentatives C de f et C’ de f -1 dans un même repère orthonormal sont symétriques par rapport à
la première bissectrice de ce repère.

 

4- Qualifications d’une fonction numérique


Soit f une fonction numérique quelconque.



On dit que f est constante si et seulement si :


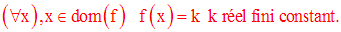
On dit que f est paire si et seulement si :


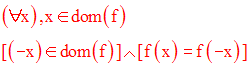
On dit que f est impaire si et seulement si :


 


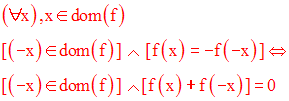
On dit que f est périodique de période t (t réel constant) si et seulement si :

 


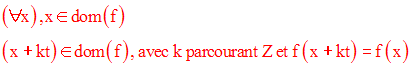
Exercice

On donne les fonctions numériques f et g définies par :

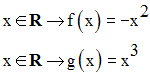
Etudie leur parité.

Cf et Cg sont leurs courbes représentatives dans un repère orthonormal.

Comment se positionne Cf par rapport à l’axe des ordonnées ?

Comment se positionne Cg par rapport à l’origine du repère ?

 

Généralisation

La courbe représentative d’une fonction numérique paire dans un repère orthonormal est symétrique
par rapport à l’axe des ordonnées.

La courbe représentative d’une fonction impaire dans un repère quelconque est symétrique
par rapport à l’origine du repère.

 

5- Etude des suites numériques


Rappelons qu’une suite numérique est une application de N ou de N* dans R.

On la note généralement :

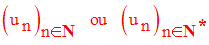
Son terme général est u n .


Dans tout ce qui suit, on notera par I, N ou N *

I étant une partie de R et une suite numérique étant une application d’une partie de R dans R, alors toute suite
numérique est une fonction numérique particulière.

Ainsi, les notions de majorants, minorants, de fonctions numériques majorées ou minorées ou bornées,
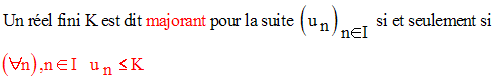
de fonctions numériques monotones, s’appliquent à une suite numérique.

 



On dira alors que la suite est majorée par K.

 



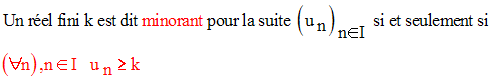
On dira alors que la suite est minorée par k.
 

 

Si une suite numérique est simultanément majorée et minorée, alors on dira qu’elle est bornée.


 

Soit une suite numérique majorée et posons M l’ensemble de ses majorants.

Si M possède un élément minimum A, alors A est dit borne supérieure de la suite et on écrit :

 

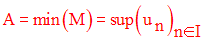
Soit une suite numérique minorée et posons N l’ensemble de ses minorants.

Si N possède un élément maximum B, alors B est dit borne inférieure de la suite et on écrit :



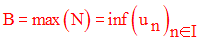
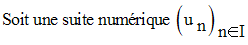
Elle sera dite croissante si et seulement si :

Elle sera dite strictement croissante si et seulement si :

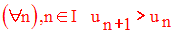
Elle sera dite décroissante si et seulement si :



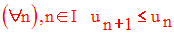
Elle sera dite strictement décroissante si et seulement si :

 


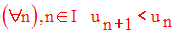
Elle sera dite monotone si elle est croissante ou décroissante ; strictement monotone si sa monotonie est stricte.

 

Limite d’une suite numérique

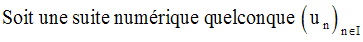
On dit que cette suite admet une limite a réelle et finie lorsque :

 


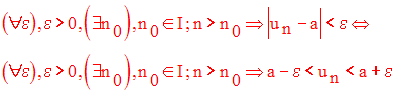
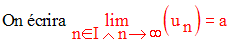
Toute suite numérique admettant une limite réelle finie est dite suite convergente.


Toute suite numérique convergente est bornée.

 

Démonstration

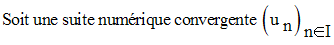
Posons a réel fini la valeur de cette limite :

Exemple :

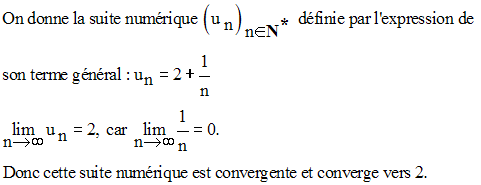
Elle est donc bornée. En effet, on a :


 

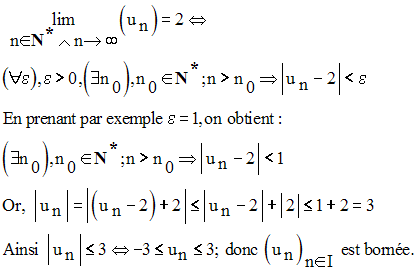
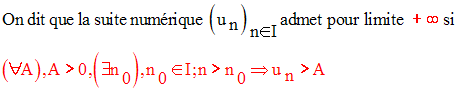
On écrit :


 

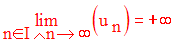
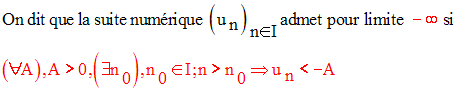
On écrit :

 

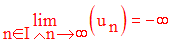
Toute suite numérique admettant une limite réelle infinie ou n’admettant pas de limites réelles finies
est dite suite divergente.

 

Exemples :


 

 

Suite oscillante

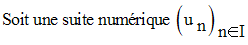
Elle est dite oscillante si, lorsque n tend vers l’infini, elle n’est pas convergente et elle ne tend
pas vers ± ∞.


Exemples :

 

Remarque :

Une suite oscillante n’étant pas convergente, est divergente.



 

Suite stationnaire

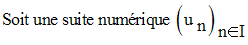
Elle est dite stationnaire, si à partir d’un certain rang n 0 , tous ses termes restent égaux à un réel fini et constant.

Exemples :

La suite numérique définie par son terme général :

 

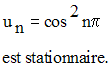
La suite numérique définie comme suit :

 

 

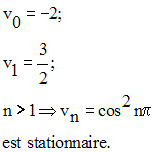
Théorèmes sur les suites convergentes
 

La somme d’un nombre fini de suites numériques convergentes est une suite numérique convergente ; sa limite est
la somme des limites de ces suites.
 

Le produit d’un nombre fini de suites numériques convergentes est une suite numérique convergente ; sa limite est
le produit des limites de ces suites.
 



 

 

 

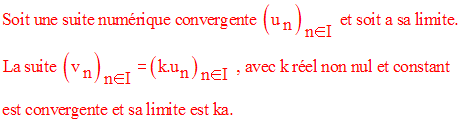
Théorème fondamental des suites monotones

Une suite numérique croissante et majorée est convergente.

Une suite numérique décroissante et minorée est convergente.

Conclusion : une suite numérique monotone et bornée est convergente.

 

Démontrons qu’une suite numérique croissante et majorée est convergente.

 

La seconde partie de ce théorème se démontre de la même façon.

 

 

Suite adjacentes

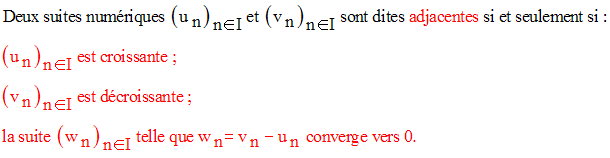
Exemple :

Les suites suivantes définies par leurs termes généraux :

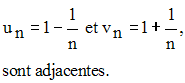
En effet on a :

 


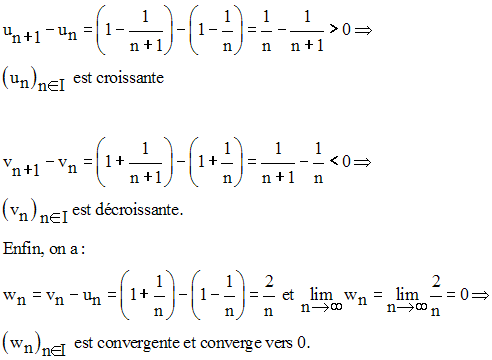
Théorème des suites adjacentes

Deux suites numériques adjacentes sont convergentes et leurs limites sont égales.

Démonstration

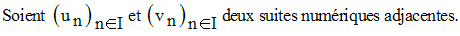
Démontrons d’abord que :

 

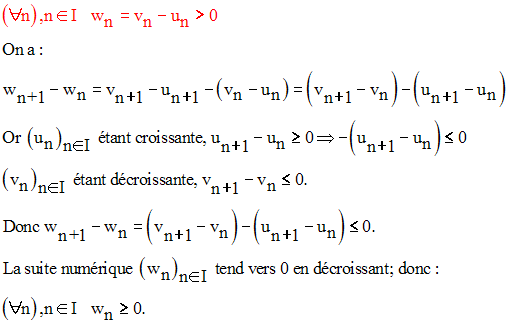
Démontrons ensuite que :


Ainsi, on a :

 

 

Suite numérique et fonction numérique
 

1)
 

Soit f une fonction numérique définie sur un intervalle réel J.

Soit ( u n ) une suite numérique d’éléments de J qui converge vers un réel a appartenant à J.

 

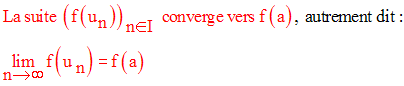
Exercice

Utilise le théorème qui précède immédiatement pour montrer par l’absurde que la fonction numérique f définie
comme suit n’est pas continue au point réel 0 :


 

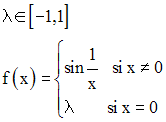
2)

Soit f une fonction numérique quelconque.



 

3)

Soit f une fonction numérique continue sur un intervalle fermé I de R.

Soient a, b deux réels appartenant à I tels que :

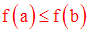
C’est le théorème dit « des valeurs intermédiaires »

Démonstration

Soient deux éléments a et b de I tels que a < b.

Supposons f (a) < f (b) et soit un point quelconque y0 tel que :

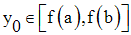
Soit m le milieu de l’intervalle fermé [a , b].

Notons a1 = a et b1 = m si f (m) ≥ y0

Notons a1 = m et b1 = b si f (m) < y0

Ainsi, on a toujours :

f (a1) ≤ y0 ≤ f (b1)

En réitérant ce procédé de construction, et par récurrence, on obtient une suite d’intervalles fermés emboîtés suivante :

 

 

 

 

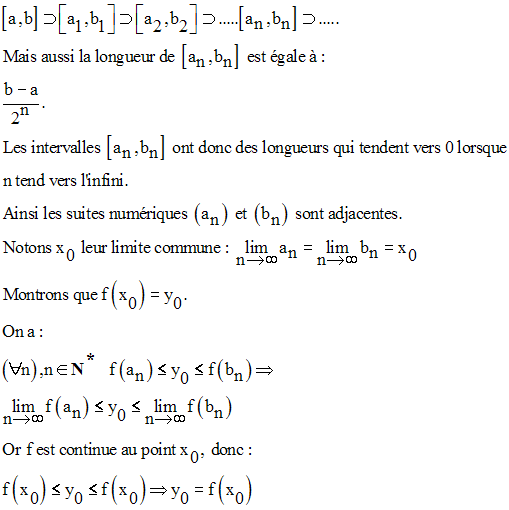
Exercices de récapitulation

 

1)

On donne la fonction numérique f définie par :

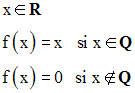
Trace sa courbe représentative C dans un repère orthonormal.

Est-elle continue en tout point réel ?

 

2)

Montre que la fonction numérique dite « racine carrée » est continue sur R+.

 

3)

On donne deux fonctions numériques f et g définies par :



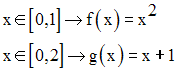
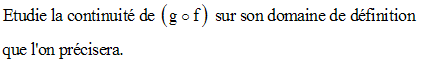
4)

 

5)

En utilisant la notion de composition de fonctions, montre que la fonction numérique f définie comme suit est continue sur R :

 

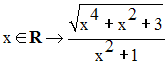
6)

On donne la suite numérique définie comme suit :

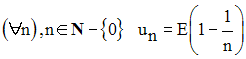
Montre qu’elle est stationnaire.




7)

Soit f une fonction numérique continue sur un intervalle réel I.

On dit qu’un point a de I est invariant par f ou est un point fixe pour f si

f (a) = a.

Montre que si l’on a :

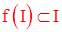
alors f admet au moins un point fixe dans I.

(Pour cela, on prendra la fonction numérique g(x) = f(x) – x et on lui appliquera le théorème des valeurs intermédiaires
après avoir montré qu’elle vérifie les conditions de ce théorème)


8)

Montre, sans calculer les racines, que l’équation :

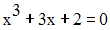
admet au moins une racine réelle.

(Pour cela on utilisera le théorème des valeurs intermédiaires)



9)

On donne la fonction numérique g définie comme suit :

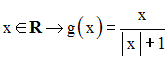
Quel est son domaine de définition ?

Montre qu’elle est impaire.

Montre qu’elle est strictement croissante sur R+ ainsi que sur R.

Calcule :

 


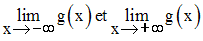
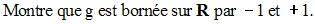
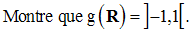
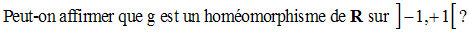
10)

Soit la fonction numérique f définie par :

 


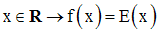
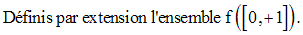
11)

Soit i la fonction numérique définie sur R par :

 



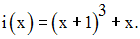
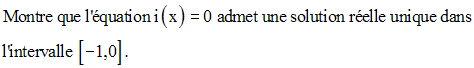
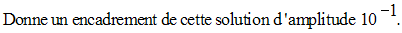
12)

Calcule les limites suivantes :

 

 

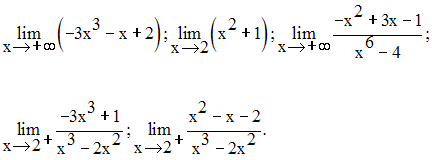
13)

Asymptotes

 Soit une fonction numérique f dont la courbe représentative dans un repère quelconque est Cf .















 

 

14)

Méthode générale pour étudier une fonction numérique f (x)

On détermine son domaine de définition ;

On étudie ses limites particulières sur ce domaine. En particulier, si ce domaine contient des intervalles possédant
des extrémités ± ∞ , on calculera ses limites lorsque x tend vers ± ∞ ;

On étudie sa continuité sur ce domaine et tout particulièrement on précisera tous ses points de discontinuité,
en calculant ses limites en ces points ;

On trouvera ses éventuelles asymptotes ;

On précisera sa qualité, le cas échéant : fonction paire ou impaire, fonction périodique (dans ce cas on calculera sa période) ;

On étudiera ses monotonies ; ceci nous permettra de déduire ses variations lorsque x parcourt le domaine de définition et
d’établir le tableau des variations de la fonction ;

Dans un repère, généralement orthonormal, on tracera sa courbe représentative, en précisant si elle possède des axes de
symétrie ou des centre de symétrie ; on tracera également, le cas échéant, ses asymptotes.

 

Etudie les fonctions numériques suivantes :

 



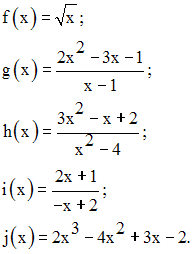
15)

Théorèmes de comparaisons

Les phrases suivantes, malgré leur imprécision au regard du langage formel des mathématiques,
ont une signification très importante.

« une fonction plus grande qu’une fonction qui tend vers + ∞ , tend vers + ∞ »

« une fonction plus petite qu’une fonction qui tend vers - ∞ , tend vers - ∞ »


Voyons ce que cela signifie dans un langage mathématique.
 












 


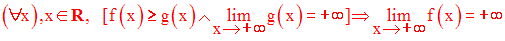
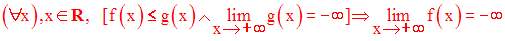
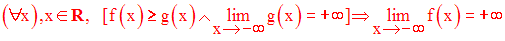
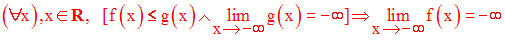
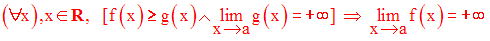
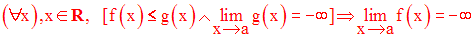
Exemple :


 

 

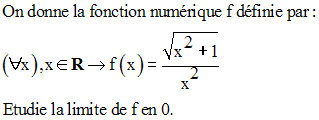
16)

Encadrement

Soient trois fonction numériques f, g, h admettant des limites en a, a réel fini.

Soit un voisinage quelconque V de a.

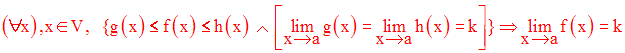
Ce théorème est connu sous le nom de « théorème des gendarmes »

Il s’applique également dans le cas où x tend vers ± ∞.

Exemple :


Exercice

 


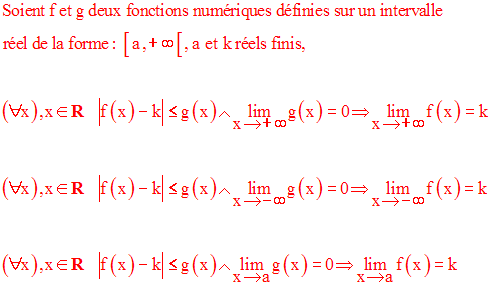
Exercice

 

 

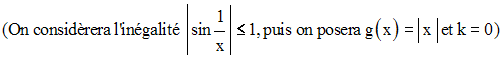
17)

Théorème de compatibilité avec l’ordre

 

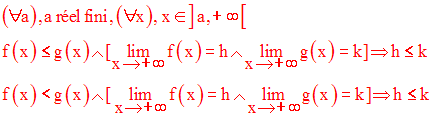
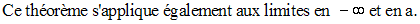
Exercice

Trouve deux fonctions numériques pour lesquelles ce théorème s’applique.

 

 

18)

Limite d’une fonction composée

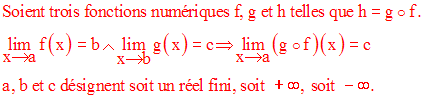
Exercice

 

 

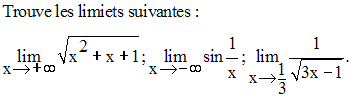
19)

On donne la fonction numérique définie par :

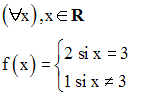
Montre que f n’est pas continue au point réel 3.

 

 


20)

Une progression arithmétique de raison r différent de 0 et une progression géométrique de raison q différent de 1
sont des suites numériques particulières.

A quels intervalles réels doivent appartenir r et q pour que ces progressions soient convergentes ? divergentes ?

 



21)

 

 

 

22)


 

 

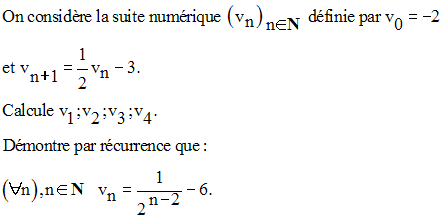
23)


 

 

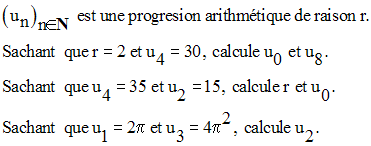
24)

 

 

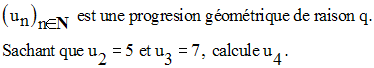
25)

 

 

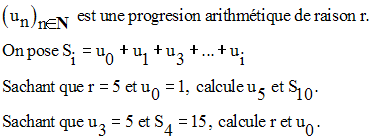
26)

 

 

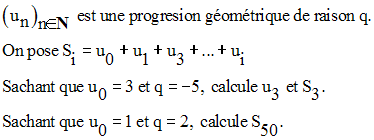
27)

 

 

28)

Deux entiers naturels a et b ont pour ppmc égal à 24 et pour pgdc égal à 4.

Trouve ces deux nombres.

 

29)

En utilisant le théorème de Bezout, montre que deux entiers naturels différents de 0 et successifs (adjacents) sont
premiers entre eux.

 

30)

 

 

31)


 

 

32)

Dans un repère orthonormal, étudie graphiquement l’existence des racines réelles de l’équation :

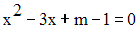
selon les valeurs du paramètre réel m.

 


 

33)

Etudie la fonction numérique f définie par :

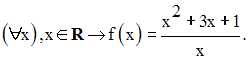
Résoudre graphiquement dans R l’équation :

m étant un paramètre parcourant R.

(On prendra comme repère un repère orthonormal)




 

34)

 


 

35)


 

 

36)

Calcule les limites suivantes :


 

 

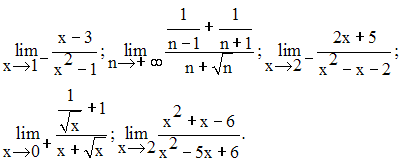
37)

En utilisant la notion de fonction composée, calcule la quantité :


 

 

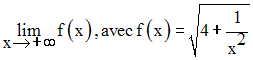
38)


 

 

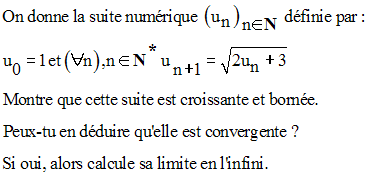
39)

On donne deux suites numériques définies comme suit :

 

 

 

retour au sommaire