INTEGRABILITE D’UNE FONCTION NUMERIQUE

FONCTIONS PRIMITIVES

1- Préliminaire

DANS TOUT CE QUI SUIT, L’INTEGRABILITE D’UNE FONCTION NUMERIQUE
EST DEFINIE AU SENS DE RIEMANN

 Deux parties A, B non vides de R sont dites adjacentes lorsqu’elles vérifient les deux conditions suivantes :

Propriété

Tout élément x de A est strictement inférieur à tout élément y de B ; donc A minore B et on a :

Tout élément y de B est strictement supérieur à tout élément x de A ; donc B majore A et on a :

Par conséquent, on a :

Or,

Donc finalement :

Mais Sup (A) et Inf (B) sont deux réels fixes ; leur différence est encore un réel fixe.

Posons donc Sup (A) – Inf (B) = k.

Montrons que k est nul.

Pour cela, nous allons d’abord montrer que k ne peut être strictement positif.

Supposons donc Sup (A) – Inf (B) = k > 0

Il existerait donc un réel k strictement positif tel que Sup (A) – Inf (B) = k ; ceci est en contradiction
avec le résultat démontré ci-dessus :

Donc k ne peut être strictement positif.

Montrons ensuite que k ne peut être strictement négatif.

Supposons donc Sup (A) – Inf (B) = k < 0

Ainsi il existerait un réel strictement positif – k  tel que pour tous éléments x et y
appartenant respectivement à A et B :

y – x ≥ – k

Ce résultat contredit la définition de l’adjacence de A et B qui énonce que :

Par conséquent, k ne peut être strictement négatif.

Conclusion

Si deux parties non vides de R sont adjacentes, alors elles possèdent une borne commune.

2- Intégrale d’une fonction en escalier

Soit une suite finie croissante de points réels :

On donne la fonction numérique f en escalier définie par :

Propriétés

a- On obtient la même somme S pour une fonction en escalier g, obtenue en changeant la valeur
de f en l’un de ses points, c.

Soit :

Démonstration

Si c est un des éléments de la suite ( x _i ), cette modification n’a aucune influence sur S.

Si c appartient à l’un des intervalles ] x _{i - 1}  , x _i [.

Dans la nouvelle somme S’, le terme h _i (x _i  – x _{i – 1}  ) de S est remplacé par :

Donc S’ = S.

b- Ainsi, on obtient la même somme S pour une fonction en escalier g, obtenue en changeant la valeur
de f en un nombre fini de points réels de [a , b].

Ces deux propriétés permettent alors d’énoncer la définition suivante :

Soit f une fonction en escalier, définie sur un intervalle [a , b], et soit une suite croissante de réels ( x _i ) :
a = x ₀ ; x ₁ ; x ₂ ; x ₃ ; … ; x _i ; x _{i + 1} ; … ; x _n = b, telle que f ait une valeur constante, h_i , sur tout
intervalle ] x _{i - 1} , x _i  [.

On nomme intégrale, au sens de Riemann, de la fonction f, sur [a , b], le réel S, indépendant
de la suite ( x _i ) considérée :

Une telle intégrale est représentée par le symbole :

qui se lit « somme de a à b de f(x) dx ».

Exemple

On a représenté f dans un repère orthonormal (Cf. figure ci-dessus) et sur l'intervalle [ – 2 , 1,3 ].

3- Intégrale d’une fonction numérique

Encadrement d’une fonction numérique par des fonctions en escaliers

Soit f une fonction numérique définie sur un intervalle borné [a , b], avec a < b.

On se propose d’encadrer f par les fonctions en escalier sur [a , b], g et h telles que g minorant f
et h majorant f.

Donc g et h seront des fonctions en escalier sur [a , b] telles que pour tout x élément de [a , b] :

g(x) ≤ f(x) ≤ h(x).

Pour que g et h existent il est nécessaire que la fonction f soit bornée sur [a , b].

Soient donc M = Sup(f) et m = Inf(f).

On a donc :

m ≤ f(x) ≤ M

Considérons une partition de [a , b] dont les éléments (Cf. figure ci-dessus) sont :

f étant définie et bornée , elle admet sur chacun des intervalles I_k , une borne inférieure m_k
et une borne supérieure M _k .

Alors, la fonction en escalier g définie sur [a , b] par :

est une fonction minorant f.

La fonction en escalier h définie sur [a , b] par :

est une fonction majorant f.

Ainsi, quelle que soit la partition de [a , b], il existe des fonctions en escalier telles que g minorant
f et des fonctions en escalier telles que  h majorant f.

Exemple

Soit la fonction numérique f définie par f(x) = x² sur [0 , 3].

On a donc f(0) = 0 ; f(1) = 1 ; f(2) = 4 et f(3) = 9.

Les fonctions en escalier g et h, définies ci-dessous, sont respectivement une fonction minorant
f et une fonction majorant f, sur [0 , 3] :

Intégration d’une fonction numérique sur un intervalle borné.

Soit f une fonction numérique définie et bornée sur un intervalle [a , b] borné, avec (a < b).

Soient sur [a , b] les fonctions en escalier g et h, g minorant f et h majorant f

(Cf. figure ci-dessus).

Remarque :

Pour simplifier, nous avons, dans notre cas, utilisé la même partition de [a , b] pour définir g et h.

Mais ce procédé n’est pas obligatoire : les partitions de [a , b] considérées pour définir g et h peuvent
être distinctes.

Les intégrales des fonctions en escalier g et h ont été déjà définies précédemment.

Elles sont telles que, quelle que soit la partition de [a , b] considérée pour les définir :

où m et M désignent respectivement la borne inférieure et la borne supérieure de f sur [a , b].

On considère les deux sous ensembles réels U et V suivants :

D’après ce qui précède, pour tous u et v respectivement éléments de U et V,

v ≥ u ou v – u ≥ 0.

Si de plus :

alors U et V sont deux sous-ensembles adjacents de R.

D’après ce que l’on a vu en préliminaire, U et V définissent donc un réel qui est la borne commune
de U et V.

Cette borne s’appelle intégrale de Riemann de f sur l’intervalle [a , b] et sera notée :

D’où la définition suivante :

Une fonction numérique f, définie et bornée sur un intervalle fermé [ a , b ], est dite intégrable sur cet
intervalle si l’ensemble des intégrales des fonctions en escalier minorant f et l’ensemble des intégrales
des fonctions en escalier majorant f sont deux parties adjacentes de R.

Intégration d’une fonction numérique définie, monotone sur un intervalle fermé

A titre d’exemple, on suppose f définie et croissante sur un intervalle réel [ a , b ].

En reprenant les notations de ce qui précède, il suffit, pour prouver que f est intégrable sur [ a , b ],
de montrer que :

Soit la partition P associée à la subdivision :

g et h sont donc associées à la même partition P de [a , b].

On a :

Le même raisonnement pourra se faire pour le cas où f est décroissante.

D’où le théorème suivant :

Toute fonction numérique f, définie et monotone sur un intervalle fermé [a , b], est intégrable
sur cet intervalle.

On démontre également les deux théorèmes suivants :

Toute fonction numérique bornée, monotone par intervalles, est intégrable.

Toute fonction numérique continue est intégrable.

4- Propriétés de l’intégrale d’une fonction numérique

Aire algébrique d’un domaine – aire géométrique ou arithmétique

Soit f une fonction numérique intégrable sur un intervalle réel fermé [a , b] et soit le domaine plan,
ensemble des points M (x , y), tels que a ≤ x ≤ b et [0 ≤ y ≤ f(x) ou f(x) ≤ y ≤ 0].

On nomme aire algébrique de ce domaine, le réel :

La figure ci-dessus montre plusieurs cas possibles d’une aire algébrique d’un domaine.

Le repère étant quelconque, supposons a < b. Soit (C) la courbe représentative de f.

Soit un point mobile M partant de a et parcourant la courbe fermée [a , b , f (b) , f (a) , a].

On convient que le sens de parcourt direct ou positif est le sens contraire des aiguilles d’une montre.

Ainsi, l’aire algébrique sera positive si le sens de parcourt de M est positif ; négative dans le cas contraire.

Considérons le dernier cas qui correspond à la subdivision n < r < t.

L’aire algébrique du domaine correspondant est :

qui est la somme algébrique des deux domaines rouge et bleu.

Souvent on nous demande de calculer l’aire géométrique dite aussi aire arithmétique correspondante.

Dans ce cas, il faudra prendre la somme des valeurs absolues des aires algébriques :

L’erreur fatale est de prendre :

Par ailleurs, une seconde erreur à éviter : omettre l’unité d’aire prise dans un repère orthogonal .

On prend l’exemple du calcul de l’aire géométrique correspondante à :

Ainsi l’aire géométrique sera :

Conseil :

Souvent les énoncés comportent une ambiguïté tel que :

Calculer l’aire du domaine limité par (C) et les droites d’équations x = a , x = b.

Aucune précision quant à la nature de cette aire !

Dans ce cas, il est conseillé de calculer les deux aires algébrique et géométrique.

Autres propriétés

Les propriétés qui suivent s’établissent facilement.
 

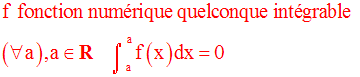
On pourra facilement démontrer les théorèmes suivants :

Démonstration de la formule de la moyenne

Pour tout réel x appartenant à [a , b], m ≤ f(x) ≤ M.

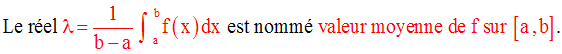
5- Fonction définie par une intégrale

Définition

Soit f une fonction numérique intégrable sur un intervalle réel [a , b].

Propriétés

Si f est définie, bornée et intégrable sur [a , b], alors F est continue sur [a , b].

Si f est continue sur [a , b], alors F est continue et dérivable sur [a , b] et sa fonction dérivée est f.

Exercices

1)

On désigne par E(x) le plus grand des entiers relatifs inférieur ou égal au réel x.

Calcule les intégrales, sur l’intervalle réel [a , b], des fonctions en escaliers suivantes :

2)

Encadre, par des fonctions en escalier, chacune des fonctions numériques f définies ci-dessous,
sur l’intervalle réel [0 , 1].
Tu choisiras des partitions de cet intervalle d’amplitude n ^{– 1} , n étant un entier naturel non nul.

3)

4)

5)

6)

6- Fonctions primitives d’une fonction numérique

Définition

Soit f une fonction numérique définie sur un intervalle réel I.

Un fonction numérique F est dite fonction primitive (ou primitive) de f sur I si et seulement si
F est dérivable sur I et sa fonction dérivée première est égale à f.

Les expressions « f est la dérivée de F » et « F est une primitive de f » sont synonymes.

Exemples :

La fonction numérique f(x) = x²  est une primitive sur R de la fonction numérique f(x) = 2x.

La fonction sinus est une primitive sur R de la fonction cosinus.

Existence de fonctions primitives

Si la fonction numérique f est continue sur un intervalle réel [a , b] et si α est un réel fixé
quelconque de [a , b], alors la fonction numérique F_α  définie sur [a , b] par :

En effet, sur [a , b], la fonction dérivée de toute fonction telle que F_α  est la fonction f.

Fonctions primitives d’une fonction numérique

Soit f une fonction numérique définie sur un intervalle réel I et soit F une fonction
primitive de f sur I.

Toute fonction numérique G définie par G(x) = F(x) + k, k réel constant quelconque, est une
primitive de f.

En effet, G’ = F’ + 0 = F’ = f.

Réciproquement, soient F et G deux fonctions primitives d’une fonction numérique
f sur un intervalle réel I.

F’ = G’ = f ; soit G’ = F’

Or nous savons que si deux fonctions F et G ont la même dérivée sur un intervalle réel I,
leur différence est une constante :

Conclusion

Si F est une primitive d’une fonction numérique définie sur I, toute fonction primitive de f
est définie par F + k où k représente une fonction numérique constante.

Conséquence immédiate

Si la fonction numérique f admet une primitive sur un intervalle réel, alors elle en admet une infinité.

Exemple :

f(x) = x³  , g(x) = x³ – 2 , h(x) = x³ + 5 sont des primitives de la fonction numérique f(x) = 3x² sur R.

Fonction primitive de valeur donnée en un point réel donné

On donne une des primitives F de la fonction numérique f sur l’intervalle réelle I.

Pour qu’une fonction primitive G = F + k (k étant un réel constant) ait, en un point a de I, une valeur
fixée ou donnée G(a), il faut et il suffit que : F(a) + k = G(a) ; ce qui donne :

k = G(a) – F(a).

La fonction primitive G, prenant en a la valeur G(a), est donc déterminée de façon unique par :

G(x) = F(x) + [G(a) – F(a)] ; d’où G(x) – G(a) = F(x) – F(a).

Exemple :

Relation entre intégrale et primitive

Soit f une fonction numérique définie et continue sur un intervalle réel

I = [u , v] et soient a, b deux réels de I.

La fonction F définie par :

est une primitive particulière de f.

Exprimons F(a) et F(b).

Calculons F(b) – F(a).

La valeur de l’intégrale de la fonction f sur [a , b] est égale à la différence entre les valeurs d’une,
quelconque, fonction primitive F, pour b et pour a.

7- Recherche des fonctions primitives d’une fonction numérique donnée

Fonctions primitives usuelles

Fonctions définies sur R

k désignant un réel constant, on a :

Fonctions définies sur un intervalle réel I

Recherche de fonctions primitives

a- Propriétés découlant de la linéarité de la dérivation.

Si les fonctions numériques f et g admettent respectivement pour primitives les fonctions F et G
sur un intervalle réel, alors la fonction (f + g) admet, sur le même intervalle, la fonction (F + G)
pour primitive.

Si la fonction numérique f admet pour primitive la fonction F sur un intervalle réel et si K est
une fonction numérique constante, alors la fonction (Kf) admet, sur le même intervalle,
la fonction (KF) pour primitive.

b- Intégration par parties

Soient u et v deux fonctions numériques dérivables, admettant des dérivées u’ et v’ continues
sur un intervalle réel I.

La dérivée du produit u.v, sur I, est telle que :

Il s’ensuit que, pour tout réel t appartenant à I :

Donc, par intégration :

Cette formule est appelée « formule d’intégration par parties ».

Exemple d’application :

Soit à déterminer les fonctions primitives de la fonction numérique f définie par :

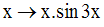
Posons, pour tout réel x :

Ce qui donne :

Par application de la formule d’intégration par parties :

ou

Finalement :

On obtient finalement :

8- L’intégration appliquée à la géométrie

Longueur d’un arc de courbe

Remarques importantes

Exemple

Calcul du périmètre d’un cercle de rayon R.

Le repère étant orthonormal, on prend le quart du cercle situé dans le premier quadrant.

Si son périmètre est l alors celui du cercle sera 4l.

Calculons donc l.

Soit un point M (x , y) quelconque de ce quart de cercle.

Exercices

a-

Calcule le périmètre de l’ellipse dont l’équation suivante est donnée dans un repère orthonormal :

b-

Dans un repère orthonormal, on donne la courbe (C) représentant la fonction numérique f définie
comme suit :

On prend sur (C) deux points A et B d’abscisses respectives 1 et 3.

Calcule la longueur de l’arc de (C), d’extrémités A et B.

Aire d’une surface plane

Désignons par (C’’) et (C’) les courbes représentant respectivement f et g, sur [a , b], dans un
repère orthogonal.

On prendra, comme vecteurs unitaires dans ce repère, les vecteurs suivants :

L’unité de mesure des longueurs sur les deux axes de ce repère est notée u.l

On se propose de calculer l’aire arithmétique A du domaine plan, ensemble
des points M(x , y) tels que :

a ≤ x ≤ b , g(x) ≤ y ≤ f(x).

1^er cas : g > 0 sur [a , b]

L’aire arithmétique A est telle que :

2^ème cas : le signe de g est quelconque sur [a, b]

Effectuons un changement de repère ; le nouveau repère se déduit de l’ancien par une
translation de vecteur :

Les courbes (C’’) et (C’) représentent dans le nouveau repère repère les fonctions u et v
telles que :

u(x) = f(x) – m et v(x) = g(x) – m

On retrouve alors le cas précédent puisque, pour tout élément x appartenant à

[a , b], v(x) est positive..

L’aire arithmétique A est donc :

L’aire arithmétique A est exprimée par la même formule que dans le premier cas.

Conclusion

Exemple :

Soient, dans un repère orthogonal les paraboles (P) et (P’) d’équations respectives :

Calculons l’aire arithmétique A qu’elles délimitent.

Le repère considéré a les caractéristiques suivantes :

En égalisant les deux équations, et en résolvant par rapport à x, on trouve les abscisses des points
d’intersection M et N de (P) et (P’).

En remplaçant x dans une quelconque des équations, par chacune de ces abscisses, on trouve
les ordonnées de M et N.

On doit trouver :

Aire d’une surface plane limitée par une courbe fermée

Dans le monde physique, pour une infinité d’objets plans, on a intuitivement la notion de surface
d’un sous-ensemble de points intérieurs à une courbe fermée (L) délimitant l’objet plan en question.

L’ébauche suivante s’applique pour le calcul de la surface de tout objet plan.

Soit un repère orthonormal quelconque :

L’unité de surface est donc l’aire d’un carré ayant pour mesure géométrique de son côté égale
à celle définie par le repère.

Une droite (D) parallèle à l’axe des abscisses coupe (L) en deux points m et n.

(D) rencontre donc la surface délimitée par (L) et l’intersection est le segment

[m , n].

Ainsi, à tout réel y est associé un segment [m , n] dont la mesure géométrique est l(y).

Désignons par S la surface délimitée par (L).

Considérons la subdivision sur l’axe des ordonnées définie comme suit :

La surface ΔS, limitée par la courbe (L) et les deux droites y = y _{i - 1} et y = y _i  est encadrée par les
aires de deux rectangles dont les bases sont situées sur ces droites et dont la hauteur commune h est
(y _i – y _{i - 1}).

On retrouve la méthode qui a permis de définir l’intégrale d’une fonction numérique encadrée par
deux fonctions en escalier.

On admettra qu’une valeur approchée de S est :

Ainsi S est égale à l’intégrale de l entre les bornes a et b :

Remarque :

On aurait pu travailler avec l’axe des abscisses et trouver que S est de la dorme :

Applications

Solutions

1)

On se propose de calculer l’aire A du quart du cercle correspondant au 1^er quadrant ;

l’aire du cercle sera donc 4 × A.

2)

Soit un point M (x , y) courant de l’ellipse.

On se propose de calculer la surface S du quart d’ellipse situé dans le 1^er quadrant.

La surface de l’ellipse sera donc 4 × S.

On sait que :

Les coordonnées de M vérifient l’équation de l’ellipse ; on a donc :

Toujours dans ce premier quadrant, l’ordonnée y de M vérifie :

 0 ≤ y ≤ b ; cette double inégalité implique que :

Il existe donc une mesure d’angle α en radian telle que :

Finalement, on a :

Remarque

Dans cette formule si l’on fait a = b, on retrouve l’aire du cercle (le cercle est une ellipse particulière
dont les mesures géométriques de ses axes sont égales).

Volume d’un solide de l’espace

Toujours dans le monde physique, pour une infinité de solides, on a intuitivement la notion de volume
d’un sous-ensemble de points intérieurs à une surface fermée (U) délimitant le solide en question.

L’ébauche suivante s’applique pour le calcul du volume de tout solide de l’espace.

Soit un repère orthonormal quelconque :

L’unité de volume est donc le volume d’un cube ayant pour mesure géométrique de son côté égale à
celle définie par le repère.

Un plan (P) parallèle au plan (xOy) coupe la surface (U) suivant la courbe (C).

A tout réel z, appelé cote du plan (P), est associé, par une application S, l’aire S(z) intérieure à (C).

Désignons par V le volume du sous-ensemble des points intérieurs à (U) et compris entre les plans de
cotes a et b (a < b).

Soit, sur l’axe (Oz) des cotes, la subdivision définie comme suit :

Là aussi on retrouve la méthode qui a permis de définir l’intégrale d’une fonction numérique encadrée
par deux fonctions en escalier.

Nous admettrons qu’une valeur approchée de V est :

Applications

1)

Volume d’un cylindre ou d’un prisme

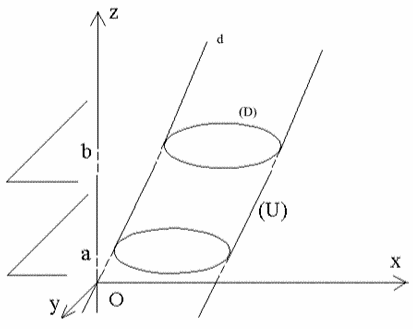
On donne une courbe plane (D) et une droite d non parallèle au plan de (D).

On nomme surface cylindrique l’ensemble (U) des points des droites parallèles à d et rencontrant (D).

La courbe (D) est appelée directrice de la surface cylindrique. Une parallèle à d rencontrant (D) est
appelée génératrice de la surface cylindrique.

Supposons d non parallèle au plan (xOy) du repère.

On nomme cylindre l’ensemble des points intérieurs à la surface cylindrique (U) et compris
entre deux plans parallèles au plan (xOy), de cotes respectives a et b, a < b.

Si (D) est un polygone, la surface cylindrique est alors nommée surface prismatique, et le cylindre
prend le nom de prisme.

Si d est orthogonale au plan (xOy), alors on dira que le cylindre ou le prisme est droit.

Deux plans parallèles au plan (xOy) coupent (U) suivant deux courbes homologues par une translation.

Quand z varie, S(z) reste donc constante et égale à S₀ .

Le volume du cylindre (ou du prisme) est donc :

2)

Volume d’un cône ou d’une pyramide

On donne une courbe plane (D) et un point O ne lui appartenant pas. On appelle surface conique
l’ensemble (U) des points des droites passant par O et rencontrant (D).

La courbe (D) est une directrice de la surface conique. Une droite passant par O et rencontrant (D)
est dite génératrice de la surface conique. Le point O est le sommet de la surface conique.

On prend le repère tel que son sommet soit confondu avec O.

On appelle cône l’ensemble des points intérieurs à la surface conique et compris entre le plan (xOy) de
cote a = 0 et un plan parallèle au plan (xOy) de cote b, b> 0.

Si (D) est un polygone, la surface conique est alors dite surface pyramidale, et le cône prend le nom
de pyramide.

La courbe (C), intersection du plan d’équation z = b et de la surface conique (ou pyramidale) est
la base du cône (ou de la pyramide) et le réel positif b est la mesure géométrique de la hauteur du
cône (ou de la pyramide).

Trouvons le volume du cône de hauteur b.

Un plan parallèle au plan (xOy), de cote z, 0 ≤ z ≤ b, coupe (U) suivant une courbe (C’),
homologue de (C) par l’homothétie :

Volume de la sphère

On donne une sphère de centre O et de rayon R.

L’origine du repère orthonormal est le point O. Le plan de cote z, telle que :

parallèle au plan (xOy), coupe la sphère suivant un cercle de rayon r, tel que :

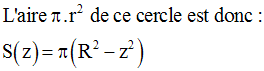
Exercices

1)

2)

Détermine, en précisant chaque fois l’intervalle d’étude, les primitives des fonctions numériques
suivantes :

3)

Calcule les intégrales suivantes :

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

Construis les courbes représentant les graphes des fonctions numériques f suivantes
(repère orthonormal) et calcule ensuite, dans chaque cas, l’aire de la surface géométrique
limitée par la courbe, l’axe (x’x) et les droites d et d’ d’équations respectives x = a et x = b :

18)

19)

20)

21)

22)

Une application à la géométrie

Volume d’un solide engendré par une surface plane tournant autour d’un axe

Lorsque Δ tourne autour de l’axe [Ox), chacun des points M décrit un cercle (C) centré sur cet axe.

L’ensemble (D) de ces cercles est une partie de l’espace dite de révolution autour de [Ox).

On dit aussi que (D) est engendrée par la révolution de Δ autour de [Ox).

Calculons le volume de (D).

Exemple d'application de cette formule :

Une autre méthode pur calculer le volume d’une sphère de rayon R.

Soit dans un repère orthonormal le quart du cercle centré sur l’origine du repère, de rayon R et situé
entièrement dans le premier quadrant.

Donc le domaine limité par ce quart de cercle et les deux axes du repère est l’ensemble ∆ suivant :

le cercle ayant pour équation :

Le volume V du solide engendré par la révolution de Δ autour de l’axe [Ox) est donc :

Conclusion

V étant le volume de la moitié d’une sphère, celui de la sphère est donc :

Exercice

Le repère étant orthonormal, calcule dans chacun des cas suivants, le volume du solide engendré par
l’ensemble Δ des points M (x , y) :

23)

Application de l’intégrale à la mécanique

Des données telles que masse, masse volumique (resp. surfacique, linéique), d’un solide,
ou telles que moment d’inertie, centre de gravité, …. sont souvent utilisées par la Mécanique ou
encore la Résistance des Matériaux : science à laquelle se réfèrent les ingénieurs du Génie Civil et
les techniciens du Bâtiment ou des Travaux Publics.

Nous allons, dans ce qui suit, aborder ces éléments du point de vue mathématique.

I- Masse d’un corps

Cas particuliers :

Si on peut assimiler le corps à une portion de surface que l’on partage en n éléments d’aire ΔS_i
et de masse Δm_i , on définira de même la masse superficielle ou surfacique ρ_i d’un quelconque
de ces éléments ; on a :

Si on peut assimiler le corps à une portion de ligne curviligne ou droite que l’on partage en
n éléments de longueur Δl_i et de masse Δm_i , on définira de même la masse linéaire ou
linéique ρ_i d’un quelconque de ces éléments ; on a :

Deux cas peuvent se présenter : f est constante en tout point P du corps, et dans ce cas on dit que
le corps est homogène ; f varie avec la position de P et est définie, continue en tout point P du corps,
et dans ce cas on dit que le corps est hétérogène.

Pour simplifier, écrivons Ω = V (resp. S ou L), selon que le corps est assimilé à un solide à trois
dimensions, à une surface ou à une ligne curviligne ou droite.

1^er cas : f constante

Le calcul de la valeur exacte de M consiste à calculer l’intégrale Ω et de  multiplier le résultat par ρ.

Exercice

Un ingénieur de la ville de Toulouse, responsable des bâtiments communaux, rédige son cahier
des charges, en vue d’un appel à la concurrence des entreprises.

Il a à calculer la masse d’une plaque de matériau mince, homogène, asimilée à un élément de
surface et ayant une masse surfacique égale à ρ.

Dans un repère orthonormal dessiné avec le logiciel de dessin AUTO CAD, cette plaque est
limitée par l’ensemble Δ des points M (x, y) défini comme suit :

Quelle est la masse M qu’aura à calculer cet ingénieur ?

2^ème cas : f fonction numérique variant avec la position du point P du corps, définie et continue
en tout point de ce corps

f variant, ne peut sortir de la somme ; le calcul de la valeur exacte de M consiste à calculer
l’intégrale de f(P)dΩ.

Exercice

Soit une plaque de matériau assimilée à un disque de centre O et de rayon r.
On suppose que la masse superficielle en un point P quelconque de cette plaque est
proportionnelle à la distance de ce point à un diamètre déterminé du disque.

Calculons la masse de cette plaque.

Choisissons un repère orthonormal de manière que son origine soit le centre O de la plaque et
l’axe des ordonnées soit porté par le diamètre en question.

La masse surfacique en un point P(x,y) quelconque de cette plaque est donc de la forme :

En raison des symétries par rapport aux axes de coordonnée, on peut se contenter de
calculer la masse du quart de la plaque située dans le premier quadrant du repère.

L’ensemble Δ des points P(x,y) est donc :

Sur l’intervalle réel [0 , r] , x est positive ; on a donc :

avec k > 0

Soit la subdivision de [0 , r] suivante :

Exercices

I-

Une barre est assimilée à un segment de droite de longueur 2l. On suppose que la masse linéique
en un point quelconque de cette barre est inversement proportionnelle au carré de la distance du point
au milieu de celle-ci.

Calcule la masse de cette barre.

II-

Un cerceau est assimilé à un cercle de rayon R. On suppose que la masse linéique en un point
quelconque P de ce cerceau est proportionnelle à la longueur de l’arc AP
(A étant un point fixé du cerceau).

Calcule la masse de ce cerceau.

III-

Soit une boule fermée de centre O et de rayon R. La masse volumique en un point quelconque
de cette boule est proportionnelle à la distance de ce point au centre O.

Calcule la masse de cette boule

(On considèrera des sphères concentriques de centre O et de rayons R_i tels que i
décrit {1, 2, …, n}, une partie de N et :

II- Centre de gravité d’un corps

En géométrie vectorielle, on a rencontré les notions de barycentre et de centre de gravité
d’un système de points matériels.

Ce point G est nommé barycentre du système de points matériels {A_i (α_i)},
i parcourant {1, 2, …, n}.

G est indépendant du choix de l’origine O ; en effet, soit un point W pou lequel le système
a pour barycentre G’. On a donc :

En particulier, si O est confondu avec G, alors :

Cas particulier : α_i =1 pour tout indice i élément de {1, 2, …, n}

Dans ce cas, G sera nommé isobarycentre du système.

Les relations deviennent :

NB :

on aurait trouvé les mêmes résultats si on avait pris tous les coefficients α_i
égaux à un réel constant non nul.

Dans le repère, si on pose X_G , Y_G , Z_G les coordonnées du barycentre G, alors on obtient,
grâce à la relation ayant servi de définir G :

En Mécanique, les coefficients α_i sont les masses des points matériels A_i .

Le point G est souvent appelé centre de gravité du système de points matériels.

Exercice

On donne dans un repère orthonormal d’origine O le système de points matériels {A₁, A₂, A₃},
les coordonnées de ces points sont respectivement (1,– 5) , (1,1) et (0,3).

Détermine le centre de gravité G de ce système.

Centre de gravité d’un corps

Ainsi on a approximativement :

Les relations donnant approximativement les coordonnées de G deviennent donc :

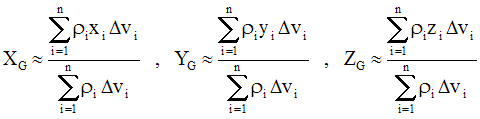
Cas particuliers :

Si on peut assimiler le corps à une portion de surface que l’on partage en n éléments d’aire ΔS_i et de
masse Δm_i , on définira de même la masse superficielle ou surfacique ρ_i d’un quelconque de ces
éléments ; on a :

Dans un repère plan, les relations donnant approximativement les coordonnées de G deviennent :

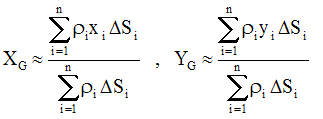
Si on peut assimiler le corps à une portion de ligne curviligne ou droite que l’on partage en
n éléments de longueur Δl_i et de masse Δm_i , on définira de même la masse linéaire ou linéique ρ_i
d’un quelconque de ces éléments ; on a :

Dans un repère linéaire ou curviligne, la relation donnant approximativement l’abscisse de G est :

Deux cas peuvent se présenter : f est constante en tout point P du corps, et dans ce cas on dit que
le corps est homogène ; f varie avec la position de P et est définie, continue en tout point P du corps,
et dans ce cas on dit que le corps est hétérogène.

Pour simplifier, écrivons Ω = V (resp. S ou L), selon que le corps est assimilé à un solide à trois
dimensions, à une surface ou à une ligne curviligne ou droite

1^er cas : f constante

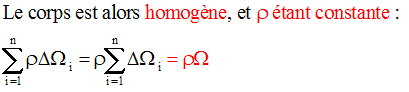
Les relations donnant approximativement les coordonnées du centre de gravité G du corps deviennent :

pour un solide à trois dimensions

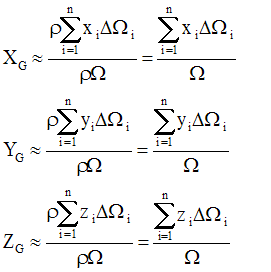
pour un corps assimilé à une surface

pour un corps assimilé à une barre rectiligne ou curviligne

Dans tous les cas abordés ci-dessus, le passage de n à l’infini permet finalement de trouver
les valeurs exactes des coordonnées de G.

Exercice

On donne dans un repère orthonormal plan les courbes représentatives (C) et (C’) des deux
fonctions numériques f₁ et f₂ définies, continues et dérivables sur l’intervalle réel [a , b],
telles que f₁(x) < f₂ (x).

De plus on suppose que ces deux courbes se coupent respectivement aux points A d’abscisse a
et au point B d’abscisse b.

Détermine le centre de gravité G du domaine Δ de ce plan défini par :

Soit {x_i}, i parcourant {1, 2,…, n}, partie de N et tel que :

{x_i} est donc une subdivision de l’intervalle réel [a , b].

Considérons un point P quelconque de Δ, d’abscisse x_P .

Considérons le rectangle R du domaine Δ de centre de gravité P (x_P , y_P) et de dimensions :

On a donc :

Son aire est :

Appliquons alors les relations donnant approximativement les coordonnées du centre de gravité G
du domaine Δ :

Application :

Une plaque mince homogène est assimilée à un quart d’ellipse représenté graphiquement comme
suit (repère orthonormal) :

L’équation cartésienne de ce quart d’ellipse est :

On a donc :

Il nous reste à calculer les intégrales ou les sommes situées aux numérateurs, c’est-à-dire :

Les coordonnées de G sont donc :

2^ème  cas : f = ρ(P) fonction numérique variant avec la position du point P du corps, définie et
continue en tout point de ce corps

f = ρ variant, ne peut sortir de la somme ; le calcul des valeurs exactes des coordonnées du centre
de gravité G du corps consiste à calculer les intégrales :

Exercices 

a-

Un opticien cherche à déterminer le centre de gravité G d’une lentille mince homogène assimilée au
domaine Δ du plan d’un repère orthonormal, défini par :

Comment procède-t-il ?

b-

Calcule le centre de gravité d’un quart de disque homogène.

c-

Un ingénieur souhaite connaître le centre de gravité d’une barre de matériaux, hétérogène.

Elle est assimilée à un segment de droite de longueur L.

Sa masse linéique ρ est, en un point M quelconque de la barre, proportionnelle au carré de la distance
de ce point à une extrémité quelconque prise comme origine.

Comment procède-t-il ?

Par ailleurs, l’architecte lui soumet une plaque mince en béton supposée homogène.

Elle est limitée par une demi couronne circulaire définie par deux disques concentriques de rayons r et R.
(r < R)

Il devra déterminer le centre de gravité de cette plaque. Comment alors procède-t-il ?

On suppose maintenant que cette plaque est hétérogène.

Sa masse surfacique ρ est une fonction numérique qui, en un point quelconque M de cette plaque,
est proportionnelle au carré de la distance de ce point au centre (fictif) de la plaque.

(ce centre est donc celui commun aux deux disques ayant délimité la plaque)

Le coefficient de proportionnalité étant k (k réel strictement positif), où se trouve donc le centre de gravité ?

Quelle est sa position relativement à celle qu’il avait dans l’hypothèse de l’homogénéité de la plaque ?

III- Moments d’inertie

Soit M un point matériel quelconque de l’espace, de masse m.

Supposons que ce point est à la distance d d’un point O, ou d’une droite Δ, ou d’un plan (P).

On appelle moment d’inertie de M par rapport au point O, ou à la droite Δ, ou

au plan (P), la quantité :

Supposons maintenant que l’on partage un corps quelconque en n petits éléments de masse Δm_i situés
à la distance d_i (supposée constante en tout point de l’élément) de O, ou de Δ, ou de (P).

On supposera que la masse volumique (resp. surfacique ou linéique) ρ en tout point de ce corps
est constante ; donc le corps est supposé homogène.

On a donc :

Le moment d’inertie de ce corps par rapport à O, ou Δ, ou (P) est égal approximativement à la somme :

Le passage de n à l’infini permettra de déterminer la valeur exacte de cette quantité.

Dans un repère orthonormal de l’espace, soit x_i , y_i , z_i  les coordonnées de l’un de ces petits éléments
(assimilé donc à un point matériel).

Les moments d’inertie du corps par rapport à l’origine O du repère, par rapport aux axes de coordonnées
et par rapport aux plans de coordonnées sont respectivement et approximativement :

Dans un repère orthonormal plan, ces relations deviennent :

Sur un axe linéaire droit, orienté d’origine O, on a :

Exercice

Montre que l’on a :

Cas particulier d’un corps homogène assimilé à une surface limitée par une courbe fermée

 1^ère Application

Une plaque homogène, de masse surfacique ρ constante, est assimilée à un disque de centre O et
de rayon r.

 Calculons son moment d’inertie par rapport à O.

 Prenons un repère orthonormal d’origine O.

Soit un élément de cette plaque assimilé à une couronne limitée par deux cercles concentriques
de centre O et de rayons :

Appliquons à cet élément la définition du moment d’inertie par rapport au centre O ; on a :

Le moment d’inertie de l’élément par rapport à O s'écrit alors :

Le moment d’inertie I_O de la plaque par rapport à O sera donc approximativement égale à la somme
des moments de tels éléments :

Le passage à l’infini donne donc :

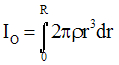
Comme ρ est constant,

Donc :

2^ème Application

Calculons le moment d’inertie, par rapport au point A, d’une tige (AB), homogène de masse linéique ρ,
de longueur L.

Pour tout élément de la tige, de longueur Δr, compris entre les points d’abscisses r₀  et r₀ + ∆r,
la masse est :

Le moment d’inertie par rapport au point A, origine du repère, est compris entre

On retrouve la méthode qui a permis de définir l’intégrale d’une fonction numérique encadrée
par deux fonctions en escalier.

Le moment d’inertie de la tige (AB) par rapport au point A est donc :

3^ème Application

Calculons le moment d’inertie par rapport à la droite (OA), d’une plaque homogène (OAB) de masse
surfacique ρ, ayant la forme d’un triangle rectangle en O, tel que OA = OB = L.

Soit i le moment d’inertie, par rapport à (OA), d’un élément quelconque de la plaque, constitué par des
points dont la distance à (OA) est comprise entre r₀ et r₀ + ∆r.

Le moment d’inertie de la plaque par rapport à (OA) sera donc :

Comme la plaque est homogène, ρ est constante et on a :

Exercice

Calcule le moment d’inertie de cette même plaque par rapport à O.

4^ème Application

On donne une demi boule homogène de masse volumique ρ, limitée par une demi sphère de
centre O et de rayon a et par un grand cercle de cette sphère.

Calculons son moment d’inertie par rapport au plan (P) du grand cercle.

Considérons la trace de cette demi boule sur un plan vertical.

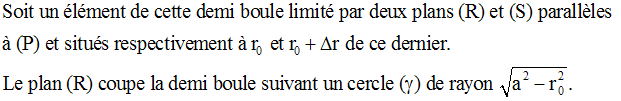
Le moment d’inertie, par rapport à (P), de cet élément est :

Le moment d’inertie, par rapport à (P), de la demi boule sera donc :

Or le volume de cette demi boule est :

Donc :

Finalement :

Exercices

I-

On donne un solide homogène de masse volumique ρ assimilé à un cône de révolution
de sommet S et de directrice un cercle (C) de centre O et de rayon a.

L’intersection du cône et d’un plan passant par (SO) est un triangle équilatéral (SAB).

Calcule le moment d’inertie de ce solide par rapport à la droite (SO).

II-

Le repère est orthonormal. Soit la plaque (P) limitée par la courbe d’équation :

l’axe (x’x), les droites d’équations respectives :

Quelle l’aire de cette plaque ?

Calcule son moment d’inertie par rapport à l’axe (x’x).

III-

retour au sommaire