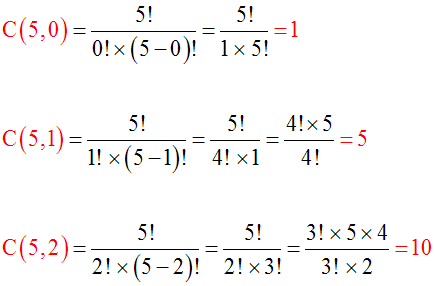
Théorie des Ensembles et Topologie - 23ème partie
Exercices
1-
On te donne l’ensemble E = {a, b, c, d ,e}
Calcule C(5 , 0) ; C(5 , 1) ; C(5 , 2) ; C(5 , 3) ; C(5 , 4) ; C(5 , 5).
Donne un exemple d’une combinaison, 3 à 3, des 5 éléments de E.
Solution
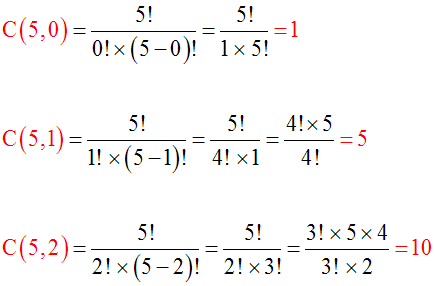
En appliquant la propriété : C(n , p) = C[n , (n – p)], on trouve :
C(5 , 3) = C[5 , (5 – 3)] = C(5 , 2) = 10
C(5 , 4) = C[5 , (5 – 4)] = C(5 , 1) = 5
C(5 , 5) = C[5 , (5 – 5)] = C(5 , 0) = 1
{b, c, e} est une combinaison, 3 à 3, des 5 éléments de E.
2-
On donne le tableau suivant :
C(1 , 0)
C(2 , 0) C(2 , 1) C(2 , 2)
C(3, 0) C(3 , 1) C(3 , 2) C(3 , 3)
C(4, 0) C(4 , 1) C(4 , 2) C(4 , 3) C(4 , 4)
C(5, 0) C(5 , 1) C(5 , 2) C(5 , 3) C(5 , 4) C(5 , 5)
C(6, 0) C(6 , 1) C(6 , 2) C(6 , 3) C(6 , 4) C(6 , 5) C(6 , 6)
…………………………………………………………..
…………………………………C(k , i) C[k , (i +1)] C[k , (i + 2)]……………
C[(k + 1) , (i + 1)]…………………
Calcule tous les termes des 6 premières lignes de ce tableau.
Que peux-tu affirmer pour les termes en rouges de type :
C[(k + 1) , (i + 1)] ; C(k , i) ; C[k , (i +1)] ?
Ce tableau s’appelle triangle de Pascal.
Chaque ligne contient tous les coefficients de l’expression :
(a + b)n, avec a, b réels quelconques et n entier naturel différent de 0.
On admettra la formule suivante dite binôme de Newton :
"a, "b, "n, a Î R, b Î R, n Î N*
(a + b) n = C(n , 0) a n b 0 + C(n , 1) a n – 1 b1 + C(n , 2) a n – 2 b2 + … + C(n , k) a n - k bk + … +
C(n , n) a n - n bn =
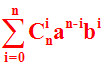

A l’aide de cette formule et du triangle de Pascal, calcule :
(a + b)3 ; (2x – 5)5
A l’aide de la formule de Newton, démontre que :
Pour tout ensemble fini E de cardinal n,
card[P(E)] = 2n
Solution
En appliquant la formule donnant le nombre de combinaisons, ainsi que ses propriétés, on trouve successivement :
1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
………….................................
En appliquant la propriété :
C(n , p) = C[(n – 1) , p] + C[(n – 1) , (p – 1)], on trouve :
C[(k + 1) , (i + 1)] = C[(k + 1 – 1) , (i + 1)] + C[(k + 1 – 1) , (i + 1 – 1)] =
C[k , (i + 1)] + C[k , i]
C’est grâce à cette relation que l’on calcule chaque ligne du tableau ; par exemple :
La troisième ligne est déduite de la seconde en appliquant la relation ci-dessus ; ainsi on a :
1 ; 1 + 2 = 3 ; 2 + 1 = 3 ; 1.
La quatrième ligne est déduite de la troisième en appliquant la même relation ; ainsi on a :
1 ; 1 + 3 = 4 ; 3 + 3 = 6 ; 3 + 1 = 4 ; 1.
Et ainsi de suite….
(a + b) 3 = C(3 , 0) a 3 b 0 + C(3 , 1) a 3 – 1 b1 + C(3 , 2) a 3 – 2 b2 + C(3 , 3) a 3 - 3 b3
Or, les termes de la troisième ligne du triangle de pascal sont :
1 ; 3 ; 3 ; 1
On obtient ainsi :
(a + b) 3 = 1 a 3 b 0 + 3 a 3 – 1 b1 + 3 a 3 – 2 b2 + 1 a 3 - 3 b3 =
(a 3 ´ 1) + 3 a 2 b + 3 a b2 + 1 (1) b3 = a3+3a2 b +3a b2 +b3
(2x – 5)5 =
[2x + (– 5)]5 = C(5 , 0) (2x)5 (– 5)0 + C(5 , 1) (2x) 5 – 1 (– 5)1 + C(5 , 2) (2x) 5 – 2 (– 5)2 +
C(5 , 3) (2x) 5 - 3 (– 5)3 + C(5 , 4) (2x) 5 - 4 (– 5)4 + C(5 , 5) (2x) 5 - 5 (– 5)5 =
(2x)5 + C(5 , 1) (2x)4 (– 5) + C(5 , 2) (2x)3 (– 5)2 + C(5 , 3) (2x) 2 (– 5)3 + C(5 , 4) (2x) (– 5)4 + (– 5)5 =
32x5 – 25 (16x4) + 250(8 x3) – 1250(4 x2) + 3125(2x) – 3125 =
32x5 – 400x4 + 2000x3 – 5000x2 + 6250x – 3125
Soit E un ensemble fini quelconque dont le cardinal est n.
On sait qu’une combinaison quelconque, p à p
( p étant inférieur à n), des n éléments de E est un sous-ensemble de E composé de p éléments.
Par conséquent, le nombre des parties de E de p éléments est égal C(n , p).
Ainsi, le nombre des parties de E à 0 élément est
C(n , 0) = 1 ; c’est la partie vide Æ de E.
Le nombre des parties de E à 1élément est C(n , 1) = n ! / [1 ! ´ (n – 1) !] = [(n – 1) ! ´ n] / [(n – 1) !] = n.
Le nombre des parties de E à 2 éléments est C(n , 2).
Le nombre des parties de E à k éléments (k inférieur à n) est C(n , k).
Ainsi de suite…jusqu’à C(n , n) = 1 qui est le nombre des parties de E ayant n éléments ; en effet, c’est la partie pleine : E.
Le nombre total des parties de E est donc égal à :
C(n , 0) + C(n , 1) + C(n , 2) + C(n , 3) + … + C(n , k) + … + C(n , n)
Dans le binôme de Newton, en faisant a = b = 1, on obtient :
(1 + 1)n = 2n = C(n , 0) + C(n , 1) + C(n , 2) + C(n , 3) + … + C(n , k) + … + C(n , n)
Or, le cardinal de P(E) est le nombre :
C(n , 0) + C(n , 1) + C(n , 2) + C(n , 3) + … + C(n , k) + … + C(n , n)
Donc, finalement on obtient :
card[P(E)] = 2n
Fin de la deuxième série
Théorie des Ensembles et Topologie - 24ème partie
NOTIONS ELEMENTAIRES DE LA THEORIE DES ENSEMBLES ET DE TOPOLOGIE
(Troisième série)
1. Relation d’équivalence sur un ensemble
On donne un ensemble E non vide quelconque. Soit Ω une relation dans E.
On dira que W est réflexive si et seulement si :
"x, x Î E x W x
Exemple :
L’égalité, notée =, dans N est réflexive car tout entier n est égal à lui-même.
On écrit n = n.
On dira que W est symétrique si et seulement si :
"x, "y, x Î E, y Î E x W y Þ y W x
Exemple :
L’égalité dans N est symétrique puisque pour tous entiers p et n, on a :
p = n Þ n = p
On dira que W est antisymétrique si et seulement si :
"x, "y, x Î E, y Î E (x W y Ù y W x) Þ x = y
Exemples :
Il est évident que l’égalité dans N est antisymétrique.
Soit maintenant la relation « … divise… » définie dans N*.
On notera « | » cette relation.
Ainsi « 2 divise 4 » sera noté : 2 | 4.
On démontre que cette relation est antisymétrique.
Soient deux entiers non nuls quelconques a, b.
Si a | b alors il existe au moins un entier q non nul tel que b = aq.
Si b | a alors il existe au moins un entier q’ non nul tel que a = bq’.
Donc b = aq = (bq’)q = b(qq’) et ceci implique que
1 = qq’ puisqu’on peut simplifier par b non nul.
Dans N* , l’équation qq’ = 1 n’est vraie que pour
q = q’ = 1 et ainsi a = b.
Conclusion :
a | b et b | a implique a = b ; donc la relation | définie dans N* est antisymétrique.
On dira que W est transitive si et seulement si :
"x, "y, "z, x Î E, y Î E, z Î E
(x W y Ù y W z) Þ x W z
Exemple
L’égalité dans N est transitive.
Exercice
Montre que la relation de divisibilité dans N* , notée « | », est transitive.
On dira que Ω est une
relation d’équivalence sur un
ensemble E
si et seulement si
elle
est
simultanément
réflexive
Exemple
L’égalité dans N est à la fois réflexive, symétrique, transitive. Donc elle est, dans N, une relation d’équivalence.
Exercice
La relation de divisibilité dans N* , notée « | », est-elle une relation d’équivalence ?
Soit Ω une relation d’équivalence sur un ensemble E.
Pour tout élément a de E, on appelle classe d’équivalence de a, la partie de E :
C(a) = {xÎ E ; x Ω a}
(Ici, le symbole « C(a) » correspond à l’élément « a » surligné qui se lit « a barre » et qui s'écrit :
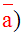
On peut facilement montrer l’équivalence logique suivante :
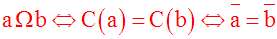
On démontre que la famille [C(a)]a Î E constitue une partition de E.
"a, a Î E C(a) est différente de l'ensemble vide.
En effet, a est un élément appartenant à C(a), puisque Ω est réflexive.
Donc C(a) n’est pas vide.
Par ailleurs, il est évident que l’on ait :
Èa Î E C(a) = E
(Ici, l’écriture « Èa Î E C(a) » se lit « union des C(a), a parcourant E »)
Enfin, on a :
C(a) ¹ C(b) Þ C(a) Ç C(b) est vide
En effet, on suppose qu’il existe au moins un élément x appartenant à C(a) et C(b).
Dans ce cas, on a x Ω a et x Ω b, ceci implique :
(a Ω b)
puisque Ω est symétrique et transitive, donc C(a) et C(b) sont deux classes d’équivalence égales ; ce qui est contraire à l’hypothèse.
Conclusion :
C(a) Ç C(b) est vide
Exercice
Montre que la réciproque est vraie, c’est-à-dire :
E étant un ensemble non vide quelconque et (Aλ)λ Î L étant une partition de E, alors la relation Ω sur E définie par :
a Ω b Û ( $λ, λ Î L, a Î Aλ Ù b Î Aλ)
est une relation d’équivalence sur E.
L’ensemble des classes d’équivalence est appelé ensemble quotient de E par Ω.
Cet ensemble sera noté :
E / Ω
Théorie des Ensembles et Topologie - 26ème partie
4.4.0
On donne A un ensemble non trivialement ordonné par une relation, notée ≤.
Montre que la relation R sur A définie par :
x R y Û (x £ y Ù x ¹ y)
est un ordre strict sur A.
4.1
n étant un nombre entier non nul, la somme suivante :
Sn = 1.2.3 + 2.3.4 + … + n(n + 1)(n + 2)
Est-t-elle égale à :
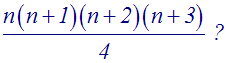
Tu raisonneras par récurrence sur n.
5.
Soit B un ensemble strictement ordonné par une relation, notée <.
5.0
Montre que la relation S sur B définie par :
x S y Û (x < y Ú x = y)
est une relation d’ordre sur B.
5.1
Montre par récurrence sur n (n entier naturel) que :
"n, n ³ 3 2n2 > (n + 1)2
"n, n ³ 5 2n > n2
Solution
Pour n = 3, 2(3)2 = 18 et (3 + 1)2 = 16 ; donc pour n = 3, on a :
18 > 16
La propriété est vérifiée pour n = 3.
On suppose qu’elle l’est pour n ³ 3. On démontre qu’elle l’est également pour (n + 1).
On a :
2(n + 1)2 = 2(n2 + 2n + 1) = 2n2 + 4n + 2 > 2n2 + 4n + 1
Or, 2n2 > (n + 1)2.
Donc, 2n2 + 4n + 1 > (n + 1)2 + 4n + 1.
Ainsi, 2(n + 1)2 > (n + 1)2 + 4n + 1 qui peut s’écrire également :
2(n + 1)2 > (n + 1)2 + 2(n + 1) + 2n – 1
Or, on a 2n > 2 implique 2n – 1 > 1.
Donc, on a :
2(n + 1)2 > (n + 1)2 + 2(n + 1) + 1, soit :
2(n + 1)2 > [(n + 1) + 1]2
Ainsi, la propriété est vraie pour (n + 1), avec (n ³ 3).
Pour n = 5, 25 = 32 et 52 = 25 ; donc 25 > 52 et la propriété est vérifiée.
On suppose qu’elle l’est pour n ³ 5 et on démontre qu’elle l’est également pour (n + 1).
On a :
2n + 1 = 2 . 2n
Or, 2n > n2.
Donc, 2n + 1 = 2 . 2n > 2n2
D’après la propriété précédente, on a :
2n2 > (n + 1)2
Donc, 2n + 1 = 2 . 2n > 2n2 > (n + 1)2
Ainsi, la propriété est vraie pour (n + 1), (n ³ 5).
6. Congruences
6.0
Soit N l’ensemble des entiers naturels.
Soit n un élément quelconque de N, différent de 0.
Deux entiers naturels quelconques a, b sont dits congrus modulo n, et on écrit :
a º b (modulo n)
si et seulement si la division de a, b par n donne le même reste.
Supposons a > b.
« La division de a et b par n donne le même reste r » est logiquement équivalente à « il existe au moins k1 et k2 deux entiers naturels tels que :
a = k1 n + r et b = k2 n + r ou a – b = (k1 – k2 )n »
Posons k1 – k2 = k.
Puisque a > b, k1 – k2 = k > 0.
On obtient ainsi la tautologie:
a º b (modulo n) Û ($ k, k Î N a – b = kn)
Exemples :
La division de 17 et de 29 par 3 donne 2 pour reste ; alors on a :
17 º 29 (modulo 3)
16 et 5 ne sont pas congrus modulo 2 ; en effet, la division de 16 par 2 donne pour reste 0 et la division de 5 par 2 donne pour reste 1.
Théorie des Ensembles et Topologie - 30ème partie
Généralisation
Dans tout ce qui précède, on a défini la congruence dans N.
Cette définition s’applique également à l’ensemble Z des entiers relatifs.
Soit n un entier strictement positif et nZ l’ensemble des multiples de n.
On dira
que l’entier relatif
x est
congru à
l’entier relatif
x’,
modulo n, si et
seulement si la différence
(x – x’) appartient à nZ.
Ainsi on a :
n Î N*, x Î Z, x’ Î Z
x º x’ (modulo n) Û ($k, k Î Z, x – x’ = kn)
Les classes d’équivalence sont :
C(0), C(+1), C(+2), … , C(n – 1)
L’ensemble des classes d’équivalence sera noté Z / nZ ; ainsi on a :
Z / nZ = {C(0), C(+1), C(+2), … , C(n – 1)}
On peut également définir les mêmes lois de composition internes précédemment rencontrées.
Ces lois auront les mêmes propriétés dans Z / nZ : commutativité, associativité, existences d’éléments neutres pour chacune des lois, symétrisation des éléments de Z / nZ.
De la définition de la congruence et des propriétés qui en découlent, montre les théorèmes suivants :
[a º b (modulo n) Ù c º d (modulo n)] Þ
[a + c º b + d (modulo n) Ù a – c º b – d (modulo n)]
[a º b (modulo n) Ù c º d (modulo n)] Þ
[a . c º b . d (modulo n)]
[a º b (modulo n)] Þ ["n, n Î N*+ a n º b n (modulo n)]
6.6
Résous dans Z / 5Z le système :
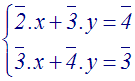
(Ici, les signes Å, Ä ont été remplacés respectivement par + et .)
Solution
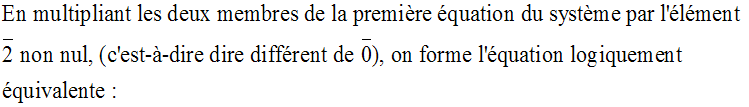
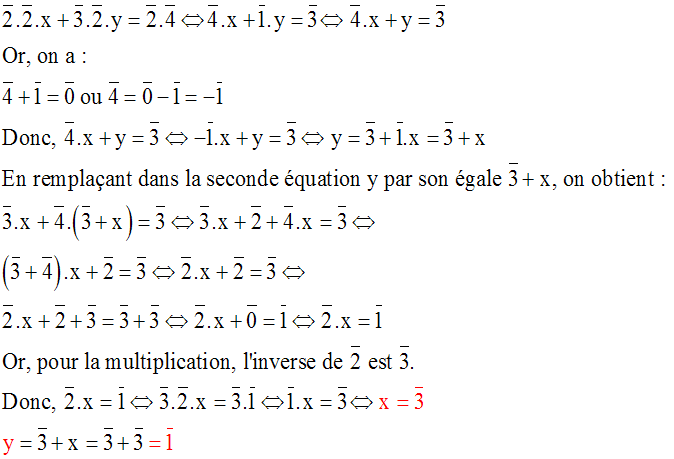
Théorie des Ensembles et Topologie - 31ème partie
6.7
Résous dans Z / 5Z le système :

(Ici, les signes Å, Ä ont été remplacés respectivement par + et .)
Solution
En additionnant membre à membre, on obtient :
[C(3) + C(2)].x + [C(2) + C(4)].y = C(1) + C(3) = C(4) Û
C(0).x + C(1).y = C(4) Û y = C(4)
C(3).x + C(2).C(4) = C(1) Û C(3).x + C(3) = C(1) Û
C(3).x + C(3) + C(2) = C(1) + C(2) Û
C(3).x + C(0) = C(3) Û
C(3).x = C(3)
D’après la table de multiplication précédente, on a :
x = C(1).
6.8
Résous dans Z / 5Z l’équation :
x2 – x – C(2) = C(0)
Solution
Compte tenu du fait que C(4) + C(1) = C(0) implique C(4) = – C(1), on a :
x2 – x – C(2) = C(0) Û x2 – C(1)x – C(2) = C(0) Û
x2 + C(4)x – C(2) = C(0) Û
x2 + C(4)x + C(4) – C(4) – C(2) = C(0)
Or,
C(4) = C(2 + 2) = C(2) + C(2) = 2C(2) et C(4) = C(2.2) = C(2).C(2) = [C(2)]2
Donc,
x2 + C(4)x + C(4) – C(4) – C(2) = C(0) Û
x2 + 2C(2)x + [C(2)]2 – C(4) – C(2) = C(0) Û
x2 + 2C(2)x + [C(2)]2 – C(1) = C(0) Û
[x + C(2)]2 = C(1)
D’après la table de multiplication, les
éléments dont le carré est égal à C(1) sont
C(1) et C(4).
Donc, on peut écrire :
[x + C(2)]2 = C(1) Û
[x + C(2) = C(1)] Ú [x + C(2) = C(4)] Û
[x + C(2) + C(3) = C(1) + C(3)] Ú [x + C(2) + C(3) = C(4) + C(3)] Û
[x + C(0) = C(4)] Ú [x + C(0) = C(2)] Û
x = C(4) ou x = C(2)
Théorie des Ensembles et Topologie - 35ème partie
7.2Soient a et b deux entiers naturels non nuls.
Soit D = pgdc (a , b).
Soit la combinaison linéaire A = ax + by, x et y parcourant N et tels que (x , y) ¹ (0 , 0).
Lorsque x et y varient, A varie et, pour certaines valeurs xp et yp , A admet une valeur minimum que l’on note m.
On a donc :
m = axp + b yp
On suppose que m ne divise pas a.
La division euclidienne de a par m donne :
a = m . q + r, avec 0 < r < m
En tirant r de cette égalité, on obtient :
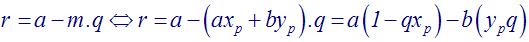
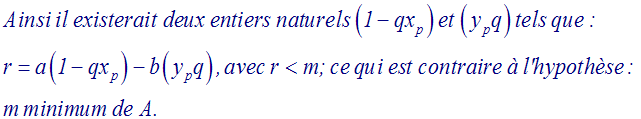
Conclusion :
m divise a.
On procède par la même démonstration par l’absurde, pour démontrer que m divise également b.
Par ailleurs, D étant le pgdc de a et b, il existe au moins deux entiers naturels non nuls, A et B, tels que : a = A . D et b = B . D
On exprime m en fonction de A, B et D :
m = D(A xp + B yp)
Donc D divise m et D £ m.
Ainsi, D et m sont diviseurs communs de a et b.
Or, D est le plus grand diviseur commun de a et b; donc m ne peut lui être strictement supérieur.
Par conséquent :
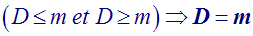
Conclusion :
[D = pgdc (a , b)] Û
[$ xp , $ yp , xp Î N, yp Î N, (xp , yp )¹ (0 , 0) et
D = axp + b yp]L’égalité D = axp + b yp est appelée Identité de Bezout.
Soit d un diviseur commun quelconque de a et b.
Montre que :
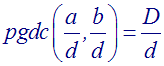
En-déduis que :
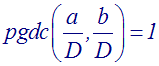
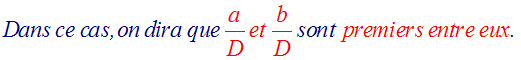
D’où la définition :
Deux nombres entiers naturels sont dits premiers entre eux si et seulement si leur pgdc est égal à 1.
On dira également que plusieurs entiers naturels sont premiers entre eux dans leur ensemble si et
seulement si leur pgdc est égal à 1.
Solution
D = pgdc (a , b) Û
[$ xp , $ yp , xp Î N, yp Î N, (xp , yp ) ¹ (0 , 0) et D = axp + b yp]
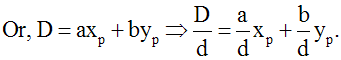
Donc, on écrit :
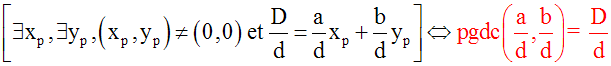
Par ailleurs, on a :
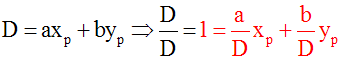
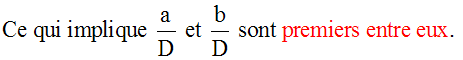
Ce résultat exprime le théorème de Bizout.
Théorie des Ensembles et Topologie - 36ème partie
7.3Montre que si un entier naturel divise le produit de deux entiers naturels et est premier avec l’un des facteurs du produit, alors il divise l’autre facteur.
C’est le théorème de Gauss.
Démonstration
Par hypothèse , on a m et n deux entiers naturels non nuls ; p un entier naturel non nul divisant m . n et premier avec m.
On démontre que p divise n.
p étant premier avec m, on peut appliquer le théorème de Bezout :
$ u , $ v , u Î N, v Î N, (u , v ) ¹ (0 , 0) et 1 = pu + mv
1 = pu + mv Þ n = pun + mvn
p divisant p et mn, divisera pun et mnv et leur somme n.
7.4
Tout entier naturel n tel que Dn = {1 , n} est appelé nombre premier.
Ainsi un entier naturel est dit premier si et seulement si ses seuls diviseurs sont 1 et lui-même.
Trouve les 20 premiers nombres premiers.
Je te laisse le soin de définir par extension l’ensemble des 20 premiers nombres premiers.
7.5
L’ensemble des multiples de p est noté Mp et celui des multiples de q, Mq .
L’ensemble des multiples communs à p et q est donc :
Mp Ç Mq
Le plus petit des éléments de cette intersection est appelé plus petit multiple commun à p et q et sera noté ppmc (p , q).
Calcule ppmc (26,39)
Je te laisse le soin de le calculer.
7.6
Soient a, b deux entiers naturels quelconques.
Posons m et n respectivement leurs pgdc et ppmc.
Montre que l’on a :
ab = mn
Solution
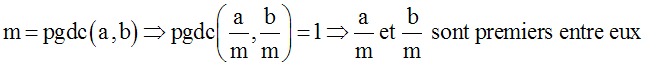
Par ailleurs, on peut écrire :
a = mq et b = mq’, avec q et q’ entiers naturels premiers entre eux.
Dire qu’un entier naturel non nul M est multiple de a, c’est dire qu’il existe au moins un entier naturel non nul k tel que M = ak = (mq)k.
Dire que M est également
multiple de b, c’est dire que b
divise (mq)k ou que mq’ divise
mqk ou encore
q’ divise qk.
q’ divisant qk et étant premier avec q, divise k, et ainsi il existe un entier naturel non nul r tel que k = rq’.
On écrit donc la forme générale des multiples communs de a et b :
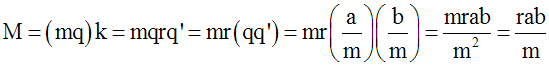
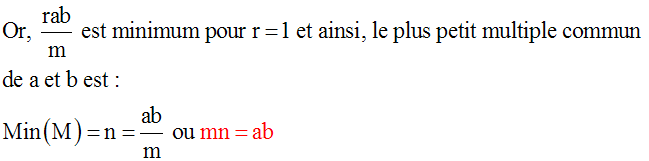
7.7
Généralisation
Les notions de pgdc et ppmc s’appliquent à plusieurs nombres entiers naturels.
Calcule :
pgdc (4, 6, 12, 36, 144) ; ppmc (4, 18, 156)
Je te laisse le soin de les calculer.
Théorie des Ensembles et Topologie - 39ème partie
PropriétésSoit une progression arithmétique de premier terme u0 et de raison r.
1)
On a :
u0 ; u1 = u0 + 1r ; u2 = u1 + r = (u0 + r) + r = u0 + 2r ; u3 = u2 + r =
(u0 + 2r) + r = u0 + 3r
Supposons que cette propriété est vraie pour n – 1 et montrons qu’elle l’est pour n.
On a donc :
un - 1 = u0 + (n – 1)r
Or, par définition, un = un - 1 + r.
Donc,
un = [u0 + (n – 1)r] + r Û
un = u0 + nr – r + r Û
un = u0 + nr
2)
u0 + un = u0 + (u0 + nr) = 2u0 + nr ;
u1 + un - 1 = u0 + r + [u0 + (n – 1)r] = 2u0 + r + nr – r = 2u0 + nr ;
u2 + un - 2 = u0 + 2r + [u0 + (n – 2)r] = 2u0 + 2r + nr – 2r = 2u0 + nr.
Supposons que cette seconde propriété est vraie pour l’indice p, p entier naturel tel que 2 < p < n :
up + un - p = 2u0 + nr
Montrons qu’elle l’est pour l’indice p + 1.
On a :
up + 1 = u0 + (p + 1)r et
u n – (p + 1) = u0 + [n – (p + 1)]r = u0 + nr – pr – r.
Donc,
up + 1 + u n – (p + 1) = u0 + pr + r + u0 + nr – pr – r = 2u0 + nr.
On dira que dans une progression arithmétique, la somme des termes équidistants est constante et est égal 2u0 + nr.
3)
Cette dernière propriété permet de calculer la somme des termes d’une progression arithmétique.
En effet, on a :
S = u0 + u1 + u2 + … + up + … + un - p + … + un - 2 + un - 1 + un
S = un + un - 1 + un - 2 + … + un - p + … + up + … + u2 + u1 + u0
En additionnant membre ces deux dernières égalités, on obtient :
2S = (u0 + un) + (u1 + un - 1) + (u2 + un - 2) + … +
(up + un - p) + … + (un - 2 + u2) + (un - 1 + u1) + (un + u0)
Mais aussi :
u0 + un = u1 + un - 1 = u2 + un - 2 = … = up + un – p = 2u0 + nr
Donc, finalement on obtient :
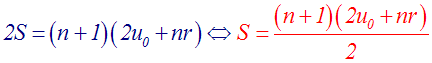
C’est la somme des (n + 1) premiers termes d’une progression arithmétique de premier terme u0 et de raison r.
On aurait pu également écrire :
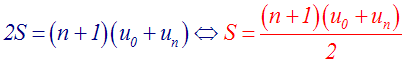
Remarque importante
Si le premier indice qui correspond au premier terme de la progression arithmétique de n termes est 1, alors on aurait, en tout, n, et non (n + 1) termes ; dans ce cas la formule donnant la somme des termes devra être réadaptée par rapport à cette nouvelle hypothèse.
Théorie des Ensembles et Topologie - 40ème partie
9.0
Calcule la somme des 100 premiers entiers naturels 0, 1, …, 99.
Solution
La raison de cette progression arithmétique est 1.
u0 = 0 et u99 = 99 Þ
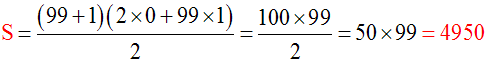
9.1
Calcule la somme des 100 premiers entiers naturels impairs et celle des 100 premiers entiers naturels pairs.
Je te laisse le soin de résoudre cet exercice.
9.2
Une progression arithmétique de n termes a pour somme S et pour dernier terme m. Calcule son premier terme a et sa raison.
Application : n = 5, S = 65 et m = 29.
Solution
Soit u0 le premier terme et r la raison.
u0 étant le premier terme et comme il y a n termes, le nième terme est un – 1.
Donc, on a :
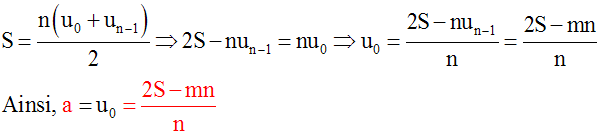
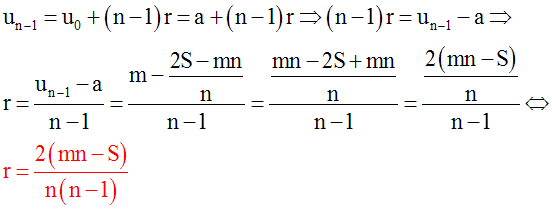
Application :
(n = 5, S = 65 et m = 29) Þ a = – 3 et r = 8
9.3
Une progression arithmétique a pour raison r = 3, pour dernier terme b = 12 et pour somme S = 30. Calcule le premier terme a et le nombre de termes n.
Solution
Soit u0 = a le premier terme et un – 1, le nième terme.
Donc, un – 1 = b.
Or, un - 1 = u0 + (n – 1)r = a + (n – 1)r.
Donc, a = un - 1 – (n – 1)r = b – (n – 1)r =
12 – 3(n – 1).
Par ailleurs, on a :

Dans cette dernière équation, on remplace a par son égale b – (n – 1)r.
On obtient :
2S – n[b – (n – 1)r] – nb = 0 Û
2S + n(n – 1)r – 2nb = 0 Û
n2 r – n(2b + r) + 2S = 0
On a donc une équation du second degré dont l’inconnue est n.
3n2 – 27n + 60 = 0
Le discriminant D de cette équation est égale à :
272 – 4 (3)(60) = 729 – 720 = 9
Les racines de cette équation existent et sont :
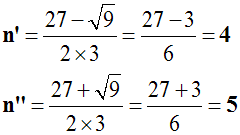
Si n = 4, alors a = 12 – 3(n – 1) = 12 – 3(4 – 1) = 3.
La progression est : 3 ; 6 ; 9 ; 12.
Si n = 5, alors a = 12 – 3(n – 1) = 12 – 3(5 – 1) = 0.
La progression est : 0 ; 3 ; 6 ; 9 ; 12.
9.4
Trouve cinq nombres en progression arithmétique connaissant leur somme 15 et la somme de leurs carrés 65.
Solution
Conseil : chaque fois qu’un énoncé fait intervenir la somme des termes d’une progression arithmétique, il est judicieux d’écrire la progression sous sa forme symétrique :
a – 2r ; a – r ; a ; a + r ; a + 2r
D’après les hypothèses de l’énoncé, on obtient :
(a – 2r) + (a – r) + a + (a + r) + (a + 2r) = 5a = 15 Þ
a = 3
(a – 2r)2 + (a – r)2 + a2 + (a + r)2 + (a + 2r)2 = 65 Û
5a2 + 10 r2 = 65 Û 10 r2 = 65 – 5a2 = 65 – 45 = 20 Û r2 = 2 Û
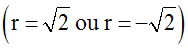

Théorie des Ensembles et Topologie - 41ème partie
Progressions géométriquesUne suite numérique (Un)n Î N est une progression géométrique si et seulement si :
"i, i Î N Ui = qUi – 1 , avec q, nombre réel non nul, différent de ± 1 et constant
La constante q est appelée raison de la progression.
Exemple :
La suite numérique définie par :
U0 = –3
U1 = –1,5
U2 = –0,75
………………
Ui = 0,5Ui – 1
est une progression géométrique de raison r = 0,5 et de premier terme U0 = –3.
Propriétés
Soit une progression géométrique de premier terme u0 et de raison q, réel non nul et différent de ±1.
1)
On a :
u0 ; u1 = qu0 = q1u0 ; u2 = qu1 = q(qu0 ) = q2u0 ; …
Supposons cette propriété vraie pour l’indice i; donc :
ui = qi u0
Montrons qu’elle l’est pour l’indice i + 1:
ui + 1 = q ui = q(qi u0 ) = (qqi )u0 = qi + 1u0
2)
Supposons, pour la suite, que cette progression possède n termes :
u0 , u1 , u2 , u3 , …, un – 1
Posons P le produit de ces n termes.
On a :
P = u0 (qu0)( q2u0) … (qiu0)( qi+1u0) …( qn – 1u0) = (u0)n q1+2+3+…+(n – 1)
On sait que l’exposant de q est la somme des termes d’une progression arithmétique de premier terme 1 et de raison 1.
Donc :
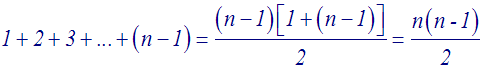
Ainsi,
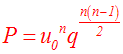
Posons S la somme des termes de la progression géométrique.
On a :
S = u0 + qu0 + q2u0 + … + qiu0 + qi+1u0 + …+ qn – 1u0 =
u0(1 + q + q2 + … + qi + qi+1 + …+ qn – 1)
q = 1 étant une racine de l’équation qn – 1= 0, alors
qn – 1 est divisible par (q – 1).
En effectuant la division de (qn – 1) par (q – 1), on trouve comme quotient exact :
1 + q + q2 + … + qi + qi+1 + …+ qn – 1
Donc, 1 + q + q2 + … + qi + qi+1 + …+ qn – 1 =
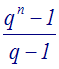
Finalement on obtient :
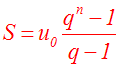
Remarque importante
Si le premier indice qui correspond au premier terme de la progression géométrique de n termes est 1, alors on aurait, en tout n, et non (n + 1) termes ; dans ce cas la formule donnant la somme des termes devra être réadaptée par rapport à cette nouvelle hypothèse.
9.5
Une progression géométrique de raison 2 se compose de six termes et sa somme est 189. Calcule le premier et le dernier terme.
Solution
Si u0 est le premier terme, alors le sixième sera u5 et on a :
u5 = q5 u0 = 25 u0 = 32 u0
Par ailleurs, on a :
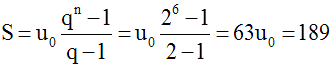
Donc, u0 = 3 et u5 = 32 u0 = 96.
9.6
Trouve trois nombres en progression géométrique connaissant leur somme 36,75 et leur produit 343.
Solution
Conseil : chaque fois qu’un énoncé fait intervenir la somme des termes d’une progression géométrique, il est judicieux d’écrire la progression sous sa forme symétrique :
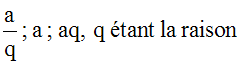
D’après les hypothèses de l’énoncé, on a :
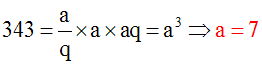
Par ailleurs, on a :
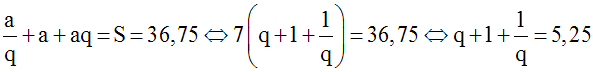
q étant non nulle, cette dernière équation en q peut s’écrire :
q2 + q – 5,25q + 1 = 0 ou
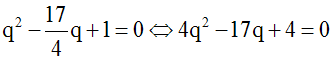
La résolution de cette équation en q donne :
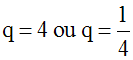
Les deux valeurs de q donnent les mêmes nombres écrits dans un ordre ou dans l’autre.
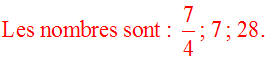
9.7

Je te laisse le soin de résoudre cet exercice.
Théorie des Ensembles et Topologie - 44ème partie
5- Topologie de la droite réelle R
R étant l’ensemble des nombres réels. Soit J l’ensemble des intervalles ouverts de R.
On dit qu’un sous-ensemble A de R est un ouvert s’il est vide, ou si pour tout x élément de A, il existe au moins un intervalle ouvert de R contenant x et contenu dans A.
L’écriture logique de cette définition est :
A est un ouvert Û
{A = Æ
ou [("x), ($I), x Î I, I Î J ; I Ì A]}Sa négation sert à démontrer qu’une partie de R n’est pas un ouvert.
Ainsi, pour démontrer qu’une partie B de R n’est pas un ouvert, il suffit de démontrer que l’on a :
{B ¹ Æ et [($x), ("I), x Î I, I Î J ; I Ë B]}
D’après la définition donnée ci-dessus, un ouvert de R est un ensemble qui est une réunion d’intervalles ouverts.
De cette définition découlent immédiatement les propriétés suivantes :
Toute réunion, finie ou non, d’ouverts de R est un ouvert de R
Toute intersection finie d’ouverts est un ouvert de R
R et l’ensemble vide sont des ouverts.
Si on note O l’ensemble des ouverts de R, alors on dira que O est une topologie de la droite réelle R.
Exemples :
1)
Tout intervalle ouvert est un ensemble ouvert.
On démontre cette tautologie.
Soit un intervalle ouvert quelconque ]a , b[ inclus dans R.
(a < b)
Soit un élément x quelconque de cet intervalle.
On a donc a < x < b.
L’intervalle ouvert I défini par :

est tel que :
il contient x
il est inclus dans ]a , b[
En effet, on a :
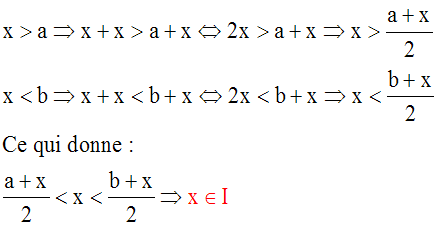
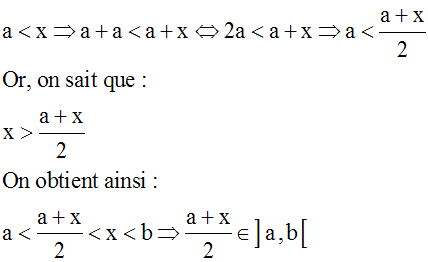
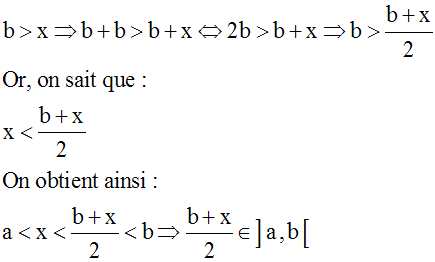
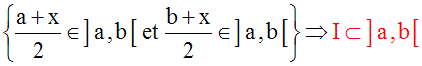
Conclusion :
{("x), ($I), x Î ]a , b[, I intervalle ouvert de R, x Î I et I Ì ]a , b[} Û
]a , b[ est un ouvert.
2)
La réunion des intervalles ouverts ]n , n+1[ où n est un élément de Z est un ouvert.
Démonstration
On vient de montrer ci-dessus que tout intervalle ouvert de R est un ouvert.
Donc, tous les intervalles de la forme ]n , n+1[, avec n parcourant Z, sont des ouverts de R.
Or, on sait que toute réunion (finie ou non) d’ouverts de R est un ouvert de R (propriété).
Donc, finalement, l’ensemble Èn Î Z ]n , n+1[ est un ouvert.
Exercices
Soit dans R l’ensemble défini par :
] – ¥ , – 1[ È ] 3 , + ¥ [
Montre que cet ensemble est un ouvert.
Je te laisse le soin de le démontrer.
Soit I = [a , b], avec a
strictement inférieur à b, un
intervalle fermé de R.
Montre que I n’est pas un
ouvert.
Montre également que tout
intervalle semi-ouvert n’est pas
un ouvert.
Solution
a Î I
Soit un réel x quelconque strictement supérieur à a.
L’intervalle ouvert ]2a – x , x[ contient a mais n’est pas contenu dans I.
En effet,
a < x Þ a – x < 0 Þ a + a – x < a Þ 2a – x < a
Ainsi, on a :
(2a – x < a < x ) Þ a Î ]2a – x , x[
Par ailleurs,
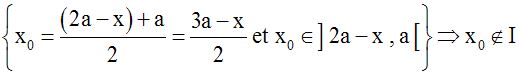
Ainsi il existe au moins un
élément x0
appartenant à ]2a – x , x[ et
n’appartenant pas à I ; par
conséquent,
]2a – x , x[
n’est pas inclus dans I.
Soit un réel y quelconque strictement inférieur à a.
L’intervalle ouvert ]y , 2a – y[ contient a mais n’est pas contenu dans I.
En effet,
a > y Þ a – y > 0 Þ a + a – y > a Þ 2a – y > a
Ainsi, on a :
(2a – y > a > y ) Þ a Î ]y , 2a – y[
Par ailleurs,
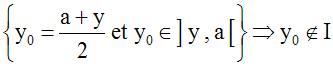
Ainsi il existe au moins un
élément y0
appartenant à ]y , 2a – y[
et n’appartenant pas à I ; par
conséquent,
]y , 2a – y[
n’est pas inclus dans I.
Conclusion :
{($a), ("J), a Î I, J intervalle ouvert de R contenant a, J Ë I} Û I n’est pas un ouvert.
Je te laisse démontrer que tout intervalle semi-ouvert n’est pas un ouvert.
Théorie des Ensembles et Topologie - 45ème partie
Remarque importante
Il est faux que l’intersection d’une infinité d’ouverts de R soit toujours un ouvert.
Par exemple, on donne les intervalles ouverts définis par :
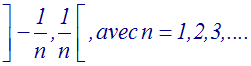


Par conséquent, lorsque n tend vers l’infini, on a :
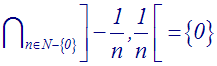
Or, le singleton {0} est tel que :
{0} ¹ Æ et [("I), 0 Î I, I intervalle ouvert de R ; I Ë {0}]

Par conséquent, ]a , b[ n’est pas inclus dans {0}.
Par conséquent, on a :
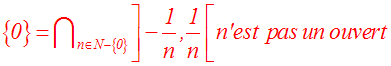
Exercice
Soient les intervalles de R définis par :
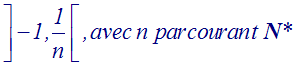
Montre que leur réunion est un ouvert et que leur intersection ne l’est pas.
Je te laisse résoudre cet exercice.
On dit qu’un sous-ensemble A de R est fermé lorsque sa partie complémentaire ðR A est un ouvert.
De chacune des trois propriétés ayant défini ci-dessus une topologie de R découle donc les propriétés suivantes :
Toute intersection, finie ou non de fermés est un fermé
Toute réunion finie de fermés est un fermé
R et l’ensemble vide sont des fermés.
Exemple :
Tout intervalle fermé de R est un fermé.
Démonstration
Soient a, b deux réels différents quelconques et soit l’intervalle fermé [a , b].
La partie complémentaire de cet intervalle réel est :
]– ¥ , a[ È ]b , + ¥[
Or, ]– ¥ , a[ et ]b , + ¥[ sont tous deux des intervalles ouverts de R ; donc ce sont des ouverts.
On sait que toute réunion d’ouverts est un ouvert ; donc, ]– ¥ , a[ È ]b , + ¥[ est un ouvert.
Ainsi, la partie complémentaire de [a , b] étant un ouvert, [a , b] est un fermé.
Remarque importante
Un ensemble peut n’être ni un ouvert, ni un fermé ; c’est le cas, par exemple, de l’ensemble Q des nombres rationnels.
Voisinage d’un point réel
On appelle voisinage d’un point x de R tout sous-ensemble V de R contenant au moins un ouvert contenant x.
Autrement dit, V est voisinage de x élément de R si et seulement si V contient un intervalle ouvert contenant x.
Exemple :
Tout ensemble ouvert A est voisinage de chacun de ses éléments.
Réciproquement, tout ensemble A qui est voisinage de chacun de ses éléments est une réunion d’intervalles ouverts, donc est ouvert.
Exercice
Soient x et y deux réels distincts quelconques et supposons que x < y.
Montre qu’il existe au moins un voisinage Vx de x et un voisinage Vy de y tels que :
Vx Ç Vy =Æ
Solution
x < y Þ ($z), z Î R, x < z < y
On considère alors les intervalles ouverts ]– ¥ , z[ et ]z , + ¥[.
]– ¥ , z[ est un ouvert contenant x et ]z , + ¥[ est un ouvert contenant y.
De plus, on a :
]– ¥ , z[ Ç ]z , + ¥[ = Æ
Ainsi, il suffit de prendre Vx égal à ]– ¥ , z[ et Vy égal à ]z , + ¥[.
Remarque
Le sens mathématique de la notion de voisinage d’un point réel diffère de celui du langage courant. En effet ce point réel peut posséder plusieurs voisinages dont R.
Théorie des Ensembles et Topologie - 47ème partie
Diamètre d’une partie de ROn appelle diamètre d’une partie A de R, la borne supérieure, notée :
d(A)
de l’ensemble des distances d(x , y) = | x – y | , x et y parcourant tous les éléments de A.
On écrit :
d(A) = sup{d(x , y) = | x – y |, x ÎA, y Î A}
On admettra que A est bornée lorsque son diamètre est un réel positif fini.
Dans le cas contraire on posera :
d(A) = + ¥
Exemple :
I = [0 , 3] et J = [4 , 9]
Donc, d(I) = 3 – 0 = 3 et d(J) = 9 – 4 = 5.
Exercice
Montre que tout intervalle I de R, fermé ou ouvert, de rayon r, a un diamètre égal à :
d(I) £ 2r
Solution
Soient a et b deux réels finis quelconques.
On suppose que a est strictement inférieur à b.
1er cas : I = [a , b]
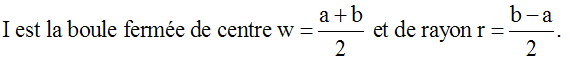
On écrit :
I = {x ; d(w , x) £ r}.
("x), ("y), x Î I, y Î I, d(x , y) £ d(x , w) + d(w , y)
Û
("x), ("y), x Î I, y Î I, d(x , y) £ d(w , x) + d(w , y)
Or, on sait que :
d(w , x) £ r et d(w , y) £ r
Donc, on a :
("x), ("y), x Î I, y Î I, d(x , y) £ 2r
2r est ainsi un majorant de l’ensemble E = {d(x , y) ; x et y parcourant I}.
De plus, pour tout e réel strictement positif, on a :
2r < 2r + e
Donc, 2r est le plus petit majorant de E et ainsi, on peut écrire :
supE = 2r ou d(I) = 2r
Je te laisse démontrer cette propriété dans le second cas où I est un intervalle ouvert.
7- Points d’accumulation, points isolés, adhérence, fermeture, intérieur
Soit A un sous-ensemble de R. Un point a appartenant à R est dit point d’accumulation de A si et seulement si tout voisinage de a contient au moins un élément de A différent de a.
On admettra sans démonstration que si a est un point d’accumulation de A, alors il existe dans tout voisinage de a une infinité de points de A différents de a.
Remarque importante
Un point d’accumulation d’une partie A de R n’appartient pas nécessairement à A.
Exercices
1)
Soit A la partie de R définie par :
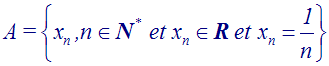
Montre que 0 est point d’accumulation de A.
Solution
Soit un voisinage V quelconque de 0.
V contient donc un ouvert ]– e , + e[ tel que e > 0 et 0 appartient à ]– e , + e[.
Or, on a :
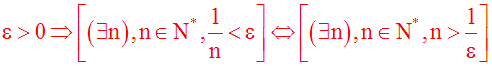
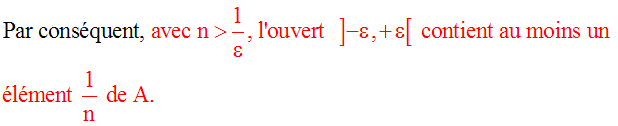
0 est donc un point d’accumulation de A.
On remarque que 0 n’appartient pas à A.
2)
Montre que 0 et 1 sont des points d’accumulation de ]0, 1[.
Je te laisse résoudre cet exercice.
On
admettra sans démonstration
que toute partie fermée de
R contient ses points
d’accumulation.
Réciproquement, toute partie
de R contenant ses
points d’accumulation est
fermé.