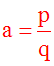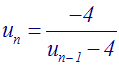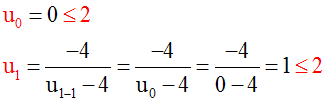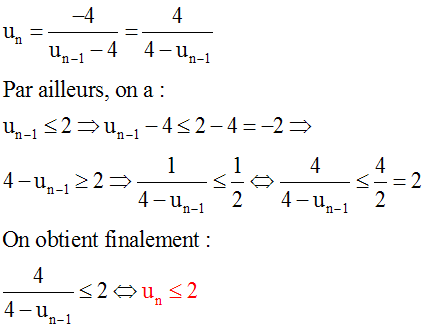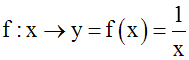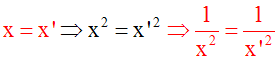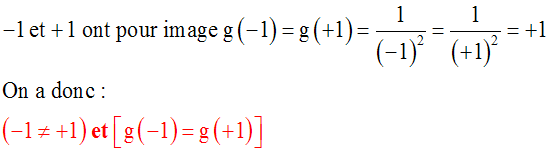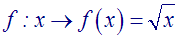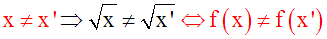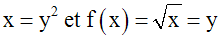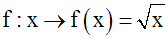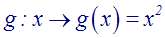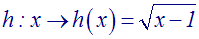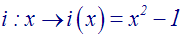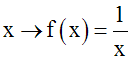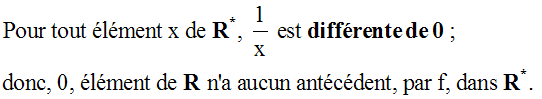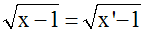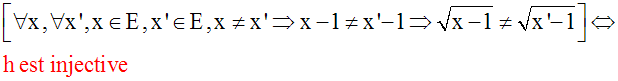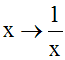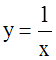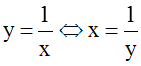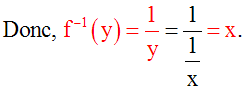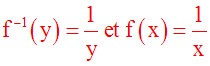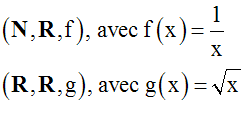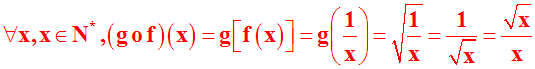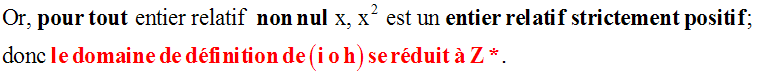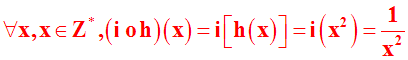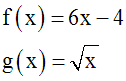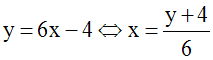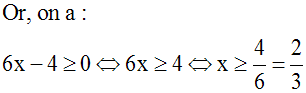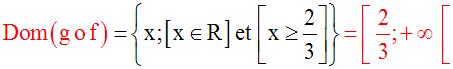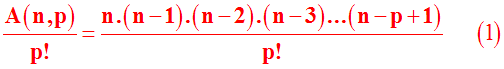GESTION DE MATHS
FLASH (8)
Théorie des Ensembles et Topologie - Neuvième partie
12. Des ensembles
particuliers
On a vu que
l’ensemble des nombres
entiers naturels
est noté N.
N privé de son
élément 0 est noté :
N*
Ainsi on a :
N*
= N – {0}
L’ensemble des
nombres entiers relatifs,
tels que
– 4, –13, +12, est
noté :
Z
Z
privé de son élément 0 est noté :
Z*
Ainsi on a :
Z*
= Z – {0}
L’ensemble des
nombres entiers relatifs
largement positifs
(resp. strictement positifs)
est noté :
Z+
(resp.
Z* + )
L’ensemble des
nombres entiers relatifs
largement négatifs
(resp. strictement négatifs)
est noté :
Z–
(resp.
Z* – )
Un nombre a est
dit rationnel si
et seulement s’il existe deux entiers relatifs p et q, avec q non nul,
tels que :
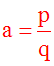
Sinon, il
sera appelé nombre irrationnel.
Exemples

L’ensemble des
nombres rationnels est noté
Q.
Exercice
Explicite
les ensembles suivants :
Q* ;
Q+ ; Q– ; Q* + ; Q* –
Je te
laisse le soin de le résoudre.
La réunion de
Q et de
l’ensemble des nombres irrationnels
est appelé ensemble des nombres réels.
Il est noté
R.
Exercice
Explicite
les ensembles suivants :
R* ;
R+ ; R– ; R* + ; R* –
Je te
laisse le soin de le résoudre.
Un nombre a est
dit nombre complexe
ou imaginaire
lorsqu’il peut se mettre sous la forme :
a +
bi,
avec a
Î
R, b
Î
R, i tel que i2 = – 1
Exemples :

L’ensemble
des nombres
complexes est noté
C.
Exercice
Explicite
l’ensemble C*.
Je te
laisse le soin de le résoudre.
Propriété
N
Ì Z
Ì Q
Ì R
Ì C
Théorie des Ensembles et Topologie - Douzième partie
A titre
d’exercice, établis les schémas sagittaux et cartésiens des correspondances h et
i données aux exemples 2 et 3 ci-dessus.
3. Relations ou
correspondances égaux
Soient deux relations f
et g définies par leurs données :
(E, F, f) et (E’, F’,
g).
On dira que
f et g coïncident
ou sont égales
si et seulement si :
E
= E’
F
= F’
Gf
= Gg
4. Relation
réciproque
On donne la donnée
d’une relation f :
(E, F, f)
On appelle
relation réciproque de f
la relation notée :
f–1
ayant pour
source F et pour
but E.
Sa donnée est
donc (F , E , f–1).
Son graphe est tel
que :
Gf–
1
Ì
F
´
E
Ù
Gf–
1 =
{(x,y) ; (x,y)
Î
F
´
E
Ù
[y = f–1
(x)]}
Exemple
Soit de nouveau les
données de l’exemple 3 ci-dessus.
E = {2,5,4,10,3} et g
la relation binaire sur E définie par :
x divise y
Avec cette
donnée, on peut définir la relation binaire g–1
réciproque de g par :
x est multiple de y
Son graphe
Gg–
1 sera
:
Gg–
1 = {(2,2) ;
(4,2) ; (10,2) ; (4,4) ; (5,5) ; (10,5) ; (10,10) ; (3,3)}
Dans E on a considéré
la deuxième correspondance i définie par :
(x
ï
y) Ù
(x < y)
Avec cette
donnée, on peut définir la relation binaire i–1
réciproque de i par :
x est multiple de y
et x est strictement supérieur à y
Son graphe
Gi–
1 sera
:
Gi–
1 = {(4,2) ;
(10,2) ; (10,5)}
Exercice
Dans les
exemples 1et2 donnés ci-dessus, explicite les relations réciproques de f et de
h. Tu expliciteras les source et but de chacune d’elles et tu définiras par
extension leurs graphes respectifs.
Je te
laisse le soin de résoudre cet exercice.
5. Applications – Fonctions
Soit la donnée
d’une relation f notée (E , F, f).
E est la source de f, F
est son but.
On dira que f est
une application de E dans F
si et seulement si
tout élément de la
source E possède par f une image et une
seule dans le but F.
Ainsi, s’il
existe au moins un
élément de la source E n’ayant pas d’image par f, alors
f n’et pas une application.
De même, s’il
existe au moins un
élément de la source E ayant deux images ou plus dans le but F, alors
f n’est pas une application.
L’image y de x
par l’application f est notée f(x)
qui se lit « image de x par f ».
L’ensemble image
Im(f) de l’application f est noté :
f(E)
Remarque
Puisque
tout élément x de E
admet, par f, une image
f(x) dans F,
Dom(f) = E.
Si E = F
alors on dira que f est une application dans
E ou dans
F.
L’application f
dans E qui à tout élément x de E applique
f(x) = x est appelée
application identique de E
et est notée :
IdE
Ainsi on a :
"x
, x
Î
E , IdE(x)
= x
Le graphe de
IdE n’est autre que l’ensemble des couples (x , y) de E × E = E2
tels que x = y.
On l’appelle diagonale
de E2 .
Exemples
Parmi les relations
suivantes f, g, h, de E = {1,2,3} vers F = {a,b,c,d} et définies par leurs
graphes respectifs:
Gf
= {(1,a) ; (1,b) ; (2,c) ; (3,d)}
Gh
= {(1,c) ; (2,b) ; (3,d)}
Gi
= {(2,b) ; (3,a)}
f n’est pas une
application car l’élément 1 de la source E possède
deux images
distinctes a et b dans le
but F ; h est une application car tout
élément de la source E possède une image et une
seule dans le but F ; i n’est pas une application
car l’élément 1 de la source ne possède aucune
image dans le but F.
Remarque
importante :
Peu importe que
les éléments du but (ensemble d’arrivée) aient ou non, par la relation, des
antécédents dans la source (ensemble de départ) ; pour que la relation soit une
application, il faut et il suffit que
tout élément de la
source ait une image et une seule
dans le but.
On appelle
suite numérique
toute application
de N (ou
N*)
dans R.
Soit la donnée (N
, R , f) d’une suite numérique.
Généralement, cette
suite est notée :
(un)n
Î
N
On a donc :
n
Î
N , n
®
f(n) = un
Î
R
Pour démontrer
que tous les termes un de cette suite numérique
vérifient une propriété P,
on utilise ce qu’on appelle la démonstration par
récurrence.
La méthode est la
suivante :
D’abord
on constate que la
propriété P est vérifiée pour le premier terme,
c’est-à-dire u0 vérifie P,
et qu’elle est également vérifiée pour le second
terme, c’est-à-dire
u1 vérifie P.
Ensuite
on suppose que P est
vérifiée pour le nième terme,
c’est-à-dire un-1 vérifie P
et enfin on démontre
qu’elle est vérifiée pour le (n+1)ième terme,
c’est-à-dire un vérifie P.
Exercice
On donne
la suite numérique (un)
de N dans R, dont le premier terme est u0
= 0
et les
termes un
et un – 1
sont liés par la relation :
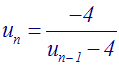
On demande
de démontrer que pour tout nombre entier naturel n, un
≤ 2.
Solution
On a :
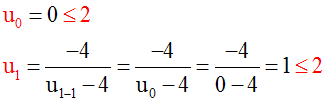
On suppose la
relation vraie pour le nième terme un - 1
et on démontre qu’elle l’est également pour le
(n+1)ième terme
un.
On a :
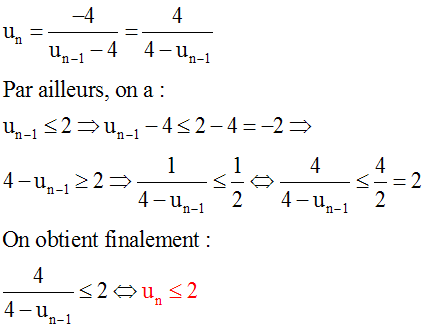
Théorie des Ensembles et Topologie - Treizième partie
Soit la donnée
d’une relation g notée (A , B, g).
On dira que g est
une fonction de A dans B
si et seulement si
tout élément de la
source A possède par g au plus
une image et une seule dans le but B.
Ainsi,
contrairement à une application, il peut exister
des éléments de la source A n’ayant aucune image
par g dans le but B.
Par contre, si un
élément de la source A possède par g une image dans le but B, cette image est
alors unique.
Ainsi, s’il
existe au moins un
élément de la source A ayant deux images ou plus par g dans le but B,
alors g n’est pas une fonction.
L’image y de x
par la fonction g est notée g(x)
qui se lit « image de x par g ».
L’ensemble image
Im(g) de la fonction g
est noté g(A).
Remarque
Puisque un élément x de
A peut ne pas avoir par g une image dans B, Dom(g) est tout simplement inclus
dans A.
Dom(g)
Ì A
Si A = B, alors
on dira que g est une fonction dans
A ou dans
B.
Si A = B = R,
alors on dira que g est une fonction
numérique.
Conclusion
Toute
application est une fonction ; mais la réciproque est fausse.
Exemple
La relation f définie
dans R comme suit :
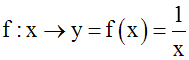
est
une fonction dans R ;
cependant, elle n’est pas une application dans
R puisque
l’élément 0 de R n’a aucune image dans R.
Dom(f) = R*.
6. Injection,
surjection et bijection
Soit f une
application de E dans F.
On sait que :
y = f(x)
Û y
Î
Im(f)
Il est évident que l’on
ait l’inclusion suivante :
Im(f)
Ì F
On dira que
l’application f est une injection
(ou une application injective)
si et seulement si tout
élément du but F possède par f et dans la source E
au plus un
antécédent.
On a ainsi la
tautologie
suivante :
f
injection
Û
{"x
,
"x’
, x
Î
E , x’
Î
E , x ≠ x’
Þ
f(x) ≠ f(x’)}
Û
{"x
,
"x’
, x
Î
E , x’
Î
E , f(x) = f(x’)
Þ
x = x’}
On a démontré en
Logique Formelle l’équivalence logique suivante :
(p
Þ
q) Û
[(Øp)
Ú
q]
Donc, les négations des
deux membres de cette équivalence logique sont logiquement équivalentes et on
peut écrire :
Ø(p
Þ
q) Û
Ø[(Øp)
Ú
q]
En appliquant une des
lois de Morgan à la dernière assertion, on obtient :
Ø(p
Þ
q) Û
Ø[(Øp)
Ú
q] Û
[Ø(Øp)
Ù
(Øq)]
Û
p Ù
(Øq)
En posant :
p
Û
[f(x) = f(x’)]
q
Û
(x = x’)
la négation de
l’assertion :
{"x
, "x’
, x Î
E , x’ Î
E , f(x) = f(x’)
Þ x = x’}
sera
donc :
{$x
, $x’
, x Î
E , x’ Î
E , [f(x) = f(x’)]
Ù (x ≠ x’)}
Ainsi on a la
tautologie
suivante :
f
n’est pas une injection
Û
{$x
,
$x’
, x
Î
E , x’
Î
E , [f(x) = f(x’)]
Ù
(x ≠ x’)}
Pour montrer
qu’une application f de E dans F n’est pas
une injection, il suffit de montrer l’existence
de deux éléments distincts
x et x’ de E tels que f(x) soit égale à f(x’).
Théorie des Ensembles et Topologie - Quatorzième partie
Exercice
On
donne la relation g dans R
définie par :

Est-ce une application ? Pourquoi ?
On
suppose maintenant que g est une
relation de R* dans
R.
Est-ce une application ? Pourquoi ?
Est-t-elle injective ? Pourquoi ?
Solution
g n’est pas une
application dans R
car
l’élément 0 de R n’aucune image
par g dans R.
Si g est une
relation de R* dans
R, alors elle est partout définie
dans R*, c’est-à-dire
tout
élément de R* possède
par g
une image
dans R.
De plus, on a :
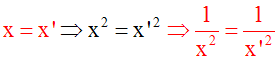
Cette image est
unique.
Donc
g est une
application de R* dans
R.
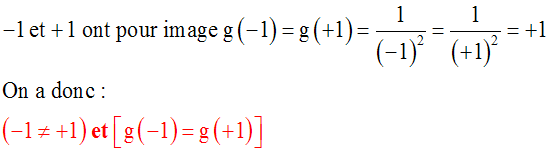
g n’est pas
injective.
Exemple d’une application injective :
Soi f l’application dans R
définie par :
f : x
®
f(x) = 2x – 1
On a,
pour tout x
et pour
tout x’ éléments de R :
x ≠ x’
Þ
2x ≠ 2x’
Þ
2x – 1 ≠ 2x’ – 1
Û
f(x) ≠
f(x’)
Donc,
f est une
injection.
On dira que
l’application f est une
surjection
(ou une
application
surjective)
si et
seulement si
tout
élément du but F possède par f et
dans la source E
au moins
un antécédent.
On a la tautologie suivante :
f
surjection
Û
Im(f) = F
On sait que :
Im(f)
Ì
F
Donc, pour que f soit surjective il
suffit de démontrer que :
F
Ì
Im(f)
Exercice
On
donne f une relation dans R
définie par :
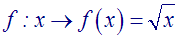
f
est-t-elle une application dans R ?
On suppose
pour la suite que f est une relation
dans R+.
f
est-t-elle une application dans
R+ ?
f
est-t-elle injective ? surjective ?
Solution
Tout nombre réel
strictement négatif
n’a
aucune image par f ;
donc f
n’est pas une application dans R.
On suppose pour la suite que f est une
relation dans R+.
Dans ce
cas, f est partout définie dans R+ :
tout
réel largement positif possède
une image
par f dans R+.
De plus, on a :

Cette image est
unique.
Donc
f est une
application dans R+.
On a,
pour tout x
et pour
tout x’ éléments de R+ :
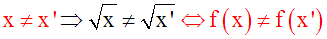
Donc,
f est une
injection.
On sait que :
Im(f)
Ì
R+
On démontre que :
R+
Ì
Im(f).
Pour tout réel y largement
positif, il existe au moins un
réel largement positif x tel que :
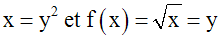
Ainsi,
tout
y de R+ possède
au moins
un antécédent y2 = x, par
f, dans R+.
y appartient
donc à Im(f).
["y
, y
Î
R+
Þ
y
Î
Im(f)]
Û
[R+
Ì
Im(f)]
[Im(f)
Ì
R+
Ù
R+
Ì
Im(f)]
Û
Im(f) =
R+
Conclusion :
f est
surjective.
On dira que
l’application f est une
bijection de E
sur F
(ou une
application
bijective)
si et seulement si f est
une
application
et
tout
élément du but F possède par f et
dans la source E
un antécédent
et un seul.
Ainsi une
application f est
bijective
si et seulement si elle est
injective et surjective.
Exemple :
L’application f dans R+
définie par :
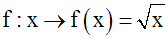
a été étudiée ci-dessus.
On a démontré qu’elle est à la fois
injective et surjective.
Donc
f est une
bijection sur R+.
Si E = F on
dira que f est une bijection
sur
E ou
sur F.
On dira également que f est une
permutation
de E ou
de F.
Théorie des Ensembles et Topologie - 15ème partie
Exercices
1-
Parmi les
applications suivantes lesquelles sont bijectives ?
f :
R*
®
R

g :
R ®
R
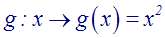
h :
E ®
R
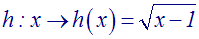
(Ici, E
est l’ensemble des réels largement supérieurs à 1)
2-
On donne
une application i de E dans F définie par :
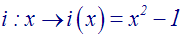
Quelles sont les
parties non vides de R auxquelles E et F peuvent respectivement
s’identifier pour que i soit une bijection ?
3-
Soient E,
F deux ensembles quelconques.
On donne
une application injective f de E dans F.
On pose
Im(f), l’ensemble des éléments de F possédant, par f, des antécédents dans E.
Montre que
f est une bijection de E sur Im(f).
Solution
1-
f : R*
®
R
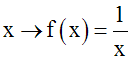
f est partout
définie dans R* ; donc, tout
élément x de R* possède
par f une image dans R.
Par ailleurs, on a :
"x ,
"x’
, x Î
R* , x’
Î R*,

Donc,
l’image, par f, de tout élément x de R*
est unique.
Conclusion :
f est une application de R*
dans R.
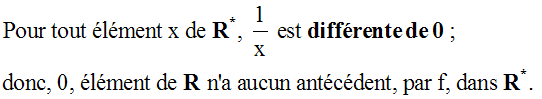
On a ainsi :
0
Ï
Im(f) Þ
R ¹
Im(f) Þ
f n’est pas surjective

f étant injective
et n’étant pas surjective, n’est pas une
bijection de R*
sur R.
Théorie des Ensembles et Topologie - 16ème
partie
g : R
®
R

g est partout
définie dans R; donc,
tout élément x
de R
possède par g une image dans R.
Par ailleurs, on a :
"x
,
"x’
, x
Î
R , x’
Î
R , x = x’
Þ
x2 = x’2
Donc,
l’image, par g,
de tout élément x de R
est unique.
Conclusion :
g est
une application dans R.
Tout élément y,
strictement négatif, de R
n’a
aucun antécédent, par g, dans R,
car il n’existe aucun réel x tel que x2
est égal à y, avec y strictement
négatif.
Par conséquent, R–
n’est pas inclus dans Im(g), et
ainsi, Im(g) est différent de R.
R
¹
Im(g)
Þ
g n’est pas surjective
–1 et +1 ont pour image g(–1) = g(+1) =
1.
Donc, on a :
(–1 ≠ +1)
et
[g(–1) = g(+1)]
g n’est pas injective.
g n’étant pas
injective et n’étant pas surjective,
n’est
pas une bijection dans
R
.
h : E
®
R

(Ici, E est l’ensemble des réels
largement supérieurs à 1)
h est partout
définie dans E; donc,
tout élément x
de E possède par h une image
dans R.
Par ailleurs, on a :
"x
,
"x’
, x
Î
E , x’
Î
E , x = x’
Þ
x – 1 = x’ – 1
Þ
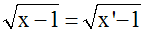
Donc,
l’image, par h,
de tout élément x de E
est unique.
Conclusion :
h est
une application de E dans R.
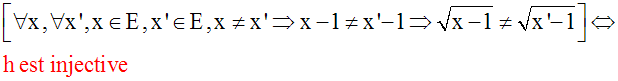
Soit y un élément quelconque de
R.
On a :

Or, la quantité (1 + y2)
est définie pour tout élément y de
R et est largement supérieure
à 1, donc appartient à E.
Conclusion :
Pour tout y élément de R, il
existe au moins x appartenant à E tel
que h(x) = y.
R est donc une partie de Im(h).
Par ailleurs, on sait que Im(h) est une partie du
but R.
[Im(h)
Ì
R
et
R
Ì
Im(h)]
Û
Im(h) = R
Im(h) étant égal à
R, h est
surjective.
h étant
simultanément injective et surjective,
est une
bijection de E sur R.
2-
On donne une application i de E dans F
définie par :
x
®
i(x) = x2 – 1
Les parties non vides de R
auxquelles E et F peuvent respectivement
s’identifier pour que i soit une
bijection sont :
E = R–
et
F = [ –1, +
¥[
ou
E =
R+
et F = [
–1, +
¥[
Théorie des Ensembles et Topologie - 17ème
partie
3-
Soient E, F deux ensembles
quelconques.
On donne une application injective
f de E dans F.
Soit Im(f) l’ensemble des éléments de F
possédant des antécédents, par f, dans
E.
f étant une application de E dans F,
tout élément x de E possède une
image et une seule dans F et
cette image appartient à Im(f).
f étant une injection, tout
élément de Im(f) possède au plus
un antécédent dans E.
Conclusion :
tout x de E possède, par f, une
image et une seule dans Im(f) et
tout y de Im(f) possède, par f,
un antécédent et un seul dans E.
Donc
f est une bijection de E sur Im(f).
Remarque :
Cette propriété
est très importante ; souvent on
l’utilise dans les problèmes pour
démontrer qu’une
application ou une fonction est
bijective.
Propriétés
Si f est une
bijection
de E sur F, alors
sa réciproque f
-1 de
F vers E
est
une
bijection
de F
sur E.
f étant une
permutation
de E,
si de plus
f = f -1
alors on dira que
f est une
involution
de E.
Exemple :
L’application (Q* ,
Q* , f) définie par :
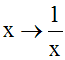
est une involution car f = f–1.
Démonstration
Il
est facile de démontrer que f est
bijective.
Je
te laisse le soin de le démontrer.
On démontre ensuite qu’elle est une
involution.
En effet, on a :
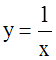
Or, x et y appartenant à Q*,
sont différents de 0 et on peut écrire :
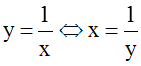
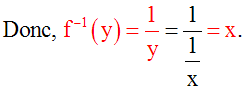
f et f–1
ont
leurs sources et leurs buts égaux à
Q*.
De plus, elles ont
la même
relation qui les définit :
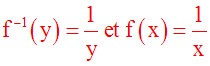
Par conséquent,
f = f–1.
7.
Composée de deux applications
On donne deux applications f et g
définies respectivement par leurs
données :
(E, F, Gf ) et (F, G, Gg
)
On a donc f une
application de E dans
F
et g une application de
F
dans G.
On remarque bien
que
le but de f
est la source de g.
De plus, on a :
Dom(g) = F
En effet, si on suppose que Dom(g) est
différent de F, alors il existerait
un élément de F qui,
n’appartenant pas à Dom(g), n’aurait
aucune image, par g, dans G ; donc
g ne serait pas une application de F
dans G.
Ce qui est contraire à l’hypothèse.
A tout élément x de E correspond une
seule image
y = f(x) dans F.
A cet élément y de F correspond une
seule image
z = g(y) dans G.
Par suite, à tout x de E
correspond une unique image z dans G
qu’on note :
g[f(x)]
On définit ainsi
une
application de E dans G
appelée
composée
de f et g
et notée :
g
o
f
qui se lit « g
rond f »
ou encore « f
suivie de g ».
On a donc :
(g
o
f)(x) = g[f(x)]
Son graphe, noté
Gg
o
f
, est l’ensemble
des couples (x, z)
tels que :
(g
o
f)(x) = z
Exemples :
1-
Soient E = {0, 5, 2} ; F = {a, c, d} et
G = {α, γ, ε}.
Soient f une application de E dans F
définie par son graphe :
Gf = {(0,a) ; (5,c) ; (2,d)}
et g une application de F dans G définie
par son graphe :
Gg = {(a, γ) ; (d, ε) ; (c,
α)}.
On a :
f(0) = a et g(a) = γ
f(5) = c et g(c) = α
f(2) = d et g(d) = ε
L’application de E dans G définie par
son graphe :
{(0, γ) ; (2, ε) ; (5, α)}
est l’application composée (g
o
f) dont la source est E et le but est G.
On
remarque que :
Dom(g) = F
2-
f étant
une bijection
de E sur F,
sa
réciproque f -1
de F vers E
est une
bijection de F sur E ;
de plus, on a :
f
-1
o
f = IdE et
f o
f -1 = IdF
Propriétés
Il est évident que
la
composition des applications n’est pas
commutative :
g
o
f ≠ f
o
g
La
composée de deux injections (resp.
surjections) est une injection (resp.
surjection).
Démonstration
Si (E,F,f) et (F,G,g) sont
surjectives, alors Im(E) =
f(E) = F et Im(F)
= g(F) = G ; ce qui entraîne évidemment
Im(g
o
f) = (g
o
f)(E) = g[f(E)] =
g(F)
= G
Si (E,F,f) et (F,G,g) sont injectives,
alors :
(g
o
f)(x) = (g
o
f)(x’)
Û
g[f(x)] = g[f(x’)]
Þ
f(x) = f(x’)
Þ
x = x’
La
composée de deux bijections est une
bijection.
Soient trois applications quelconques
f, g, h définies par leurs données :
(E, F, f) ; (F, G, g) ; (G, H, h)
On
peut facilement démontrer que :
h
o
(g
o
f) = (h
o
g)
o
f
On dira que
la
composition des applications est
associative.
A
titre d'exercice, je te laisse démontrer
cette propriété.
Théorie des Ensembles et Topologie -
19ème
partie
Exemples
1-
On donne deux fonctions
f et g définies comme suit :
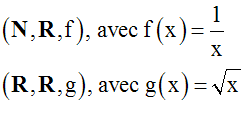
On a :
Dom(f) = N*
et Dom(g) = R+

Im(f) est donc égal à
Q* +.
Par conséquent, on a :
Im(f)
Ç Dom(g) =
Q* +
Ç
R+
= Q* +
Cette intersection est
différente de l'ensemble vide.
(g
o
f) est définie par les données suivantes :
Sa
source est N
Son
but est R
Son
domaine de définition est défini comme suit :
{x ;
[x
Î
N*]
et
[f(x)
Î
Q*
+]}
Le
domaine de définition de (g
o f) se
réduit à
N*.
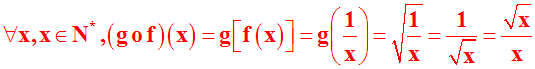
2-
On donne deux fonctions
h et i définies comme suit :

On a :
Dom(h) = Z
et Dom(i) = R*
Par ailleurs, x étant
un entier relatif quelconque, x2 est un entier relatif positif ;
donc x2 est un élément de Z+.
Im(h) est donc égal à
Z+.
Par conséquent, on a :
Im(h)
Ç Dom(i) =
Z+
Ç
R*
= Z+
*
Cette intersection est
différente de l'ensemble vide.
(i
o
h) est définie par les données suivantes :
Sa
source est Z
Son
but est R
Son
domaine de définition est défini comme suit :
{x ;
[x
Î
Z]
Ù
[h(x)
Î
Z*
+]}
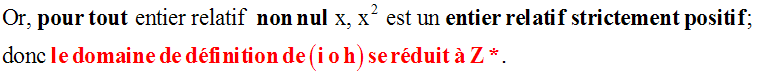
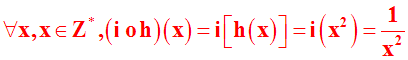
3-
On donne deux fonctions
numériques f et g définies comme suit :
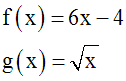
On a :
Dom(f) = R
et Dom(g) = R+
Par ailleurs, on a :
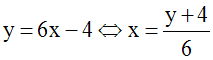

f est donc
surjective et on a Im(f) = R.
Par conséquent, on a :
Im(f)
Ç Dom(g) =
R
Ç
R+
= R+
Cette intersection est
différente de l'ensemble vide.
(g
o
f) est définie par les données suivantes :
Sa
source est R
Son
but est R
Son
domaine de définition est défini comme suit :
{x ;
[x
Î
R] et
[f(x)
Î
R+]}
Û
{x ;
[x
Î
R]
et
[6x – 4
³
0]}
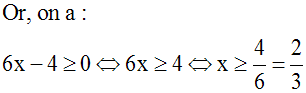
Par conséquent,
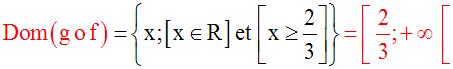

Théorie des Ensembles et Topologie -
22ème
partie
Application
Soient deux ensembles finis
quelconques E et F, tels que :
0 < p = card(E) ≤ card(F) = n
On
admettra que
le
nombre des applications
injectives de E dans F
est égal à
A(n ,
p).
Exercices
1-
On te donne A = {1, 5} et B =
{a, e, i}.
Calcule le nombre des
applications injectives de A
dans B.
Définis par extension leurs
graphes respectifs.
Solution
Soit N le nombre des
applications injectives
de A dans B.
On a:
N
= A(3 , 2)
= 3
´
2
= 6
Soient f, g, h, i, j, k ces 6
injections.
On a :
Gf
= {(1,a) ; (5,e)}
Gg=
{(1,e) ; (5,i)}
Gh
= {(1,a) ; (5,i)}
Gi
= {(5,a) ; (1,e)}
Gj
= {(1,i) ; (5,a)}
Gk
= {(1,i) ; (5,e)}
2-
On te donne l’ensemble E = {1,
a, 3, d, 5}.
Calcule le nombre des
arrangements, 2 à 2, des 5
éléments de E.
Calcule le nombre
d’arrangements, 4 à 4, des 5
éléments de E.
Calcule le nombre des
permutations de E.
Solution
Le nombre des arrangements, 2 à
2, des 5 éléments de E est :
A(5 ,
2)
= 5
´
4
= 20.
Le nombre des arrangements, 4 à
4, des 5 éléments de E est :
A(5 ,
4)
= 5
´
4
´
3
´
2
= 120.
Le nombre de permutations de E
est :
5!
= 5
´
4
´
3
´
2
´
1
= 120.
Combinaison
On donne un ensemble fini
E de n éléments.
Soit un nombre entier naturel p
tel que :
0 ≤ p ≤ n
On appelle
combinaison, p à p, des n
éléments de E
tout sous-ensemble
ou
partie
de E constitué de
p
éléments.
Ainsi, en
calculant
le
nombre de
toutes
les combinaisons possibles
d’un ensemble E fini, on
trouve
le
cardinal de l’ensemble P(E) des
parties de E.
Deux
combinaisons, p à p, distinctes
diffèrent par la nature
des éléments qui les
constituent :
aucune
considération d’ordre
n’intervient.
On se propose de calculer le
nombre des combinaisons, p à p,
des n éléments de E.
Tout arrangement, p à p, des n
éléments de E peut être
considéré comme une
permutation des p éléments d’une
combinaison, p à p ; Par
conséquent, si nous dressons la
liste des toutes les
permutations des éléments des
diverses combinaisons, p à p,
nous obtenons tous les
arrangements, p à p.
En outre, deux arrangements de
cette liste diffèrent :
- soit par la nature de
leurs éléments, s’ils ont été
obtenus à partir de deux
combinaisons distinctes ;
- soit par l’ordre de
leurs éléments, s’ils ont été
obtenus à partir de la même
combinaison.
Ainsi, chaque combinaison, p à
p, a généré (p !) arrangements,
p à p.
Le
nombre,
noté
C(n ,
p),
des
combinaisons, p à p, des n
éléments de E
est donc égal à :
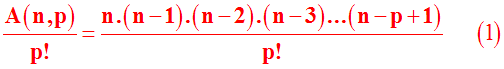
(Ici, le
symbole « C(n,
p) »
se lit « nombre
de combinaisons, p à p, de n
éléments »)
Par ailleurs, on sait que :
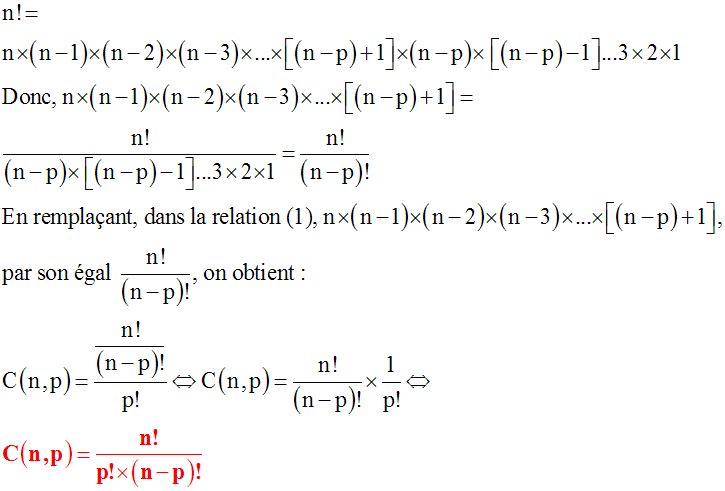
Cas particuliers :
C(n , 0) = C(n , n) = 1
Propriétés
1-
Toute combinaison, p à p, des n
éléments de E est une partie
constituée de p éléments de E.
La partie complémentaire de
cette partie est une
combinaison,
(n – p) à (n – p), des n
éléments de E.
Comme le cardinal de P(E) est un
entier pair (cette
propriété a été démontrée à
l’exercice 2), il y a donc
autant de combinaisons, p à p,
que de combinaisons,
(n – p) à (n – p), des n
éléments de E.
On a donc :
C(n , p) = C[n , (n – p)]
2-
On fixe un élément a
quelconque de E.
Les combinaisons, p à p, des n
éléments de E peuvent se
répartir en deux classes :
- L’une formée des combinaisons
qui ne contiennent pas l’élément
a : ce sont les combinaisons, p
à p, des
(n – 1) éléments autres que a
- L’autre formée des
combinaisons qui contiennent a :
on les obtient par adjonction de
a à chacune des combinaisons, (p
– 1) à (p – 1), des (n – 1)
éléments autres que a.
Par conséquent, on obtient la
relation suivante :
C(n , p) = C[(n – 1) , p] + C[(n
– 1) , (p – 1)]
retour au sommaire