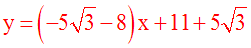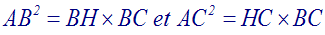
2-
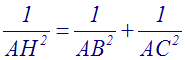
3-
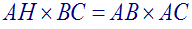
4-
Relations dans un triangle rectangle
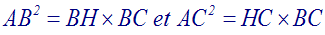
2-
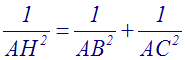
3-
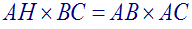
Traitons ensemble la première
question.
Les deux triangles rectangles (ABH) et (ABC) ont en commun l'angle aigu en
B; donc ils ont un angle aigu égal.
On sait que deux triangles rectangles
ayant un angle aigu égal sont semblables.
Donc (ABH) et (ABC) sont semblables.
Pour écrire la proportionnalité portant sur les mesures géométriques de
leurs côtés, on procède
comme suit :
On écrit la suite des sommets de (ABC) :
A B C
(l'ordre ici n'a aucune
importance; cependant une fois choisi on ne le change plus)
Puis en dessous, on écrit la suite des sommets de (ABH),
dans l'ordre défini comme suit : à l 'angle droit en A on
fait correspondre son égal, l'angle droit en H,
à l'angle en B on fait correspondre son égal, l'angle
B (puisque cet angle est commun), à l'angle en C on fait correspondre
son égal, l'angle en A.
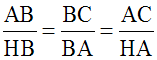
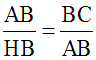
Sachant que dans une proportion le produit des moyens termes est
égal à celui des termes extrêmes, on obtient finalement :
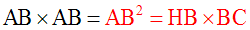
A ta plume pour le reste de l'exercice.....
douce pente
Je comprends et je retiens
A l’aide des formules suivantes que je suppose connues :
sin(a + b) = sina . cosb + cosa . sinb
sin(a – b) = sina . cosb – cosa . sinb
cos(a + b) = cosa . cosb – sina . sinb
cos(a – b) = cosa . cosb + sina . sinb
Je dois établir celles me donnant tan(a + b), tan(a – b).
J’écris donc :
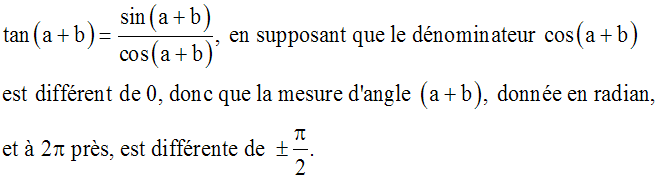
J’obtiens :

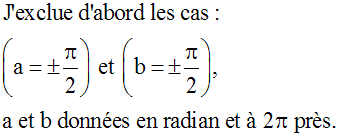
Ainsi, la quantité (cosa . cosb) est différente de 0 et je peux diviser les deux membres de la fraction ci-dessus par (cosa . cosb) ; j’obtiens :
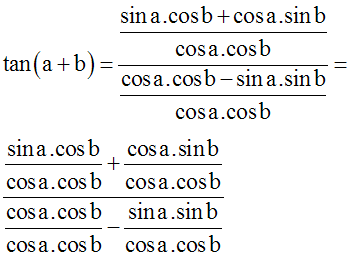
En simplifiant par cosb et cosa, j’obtiens :
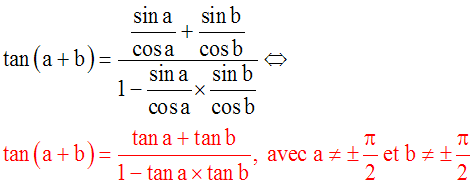
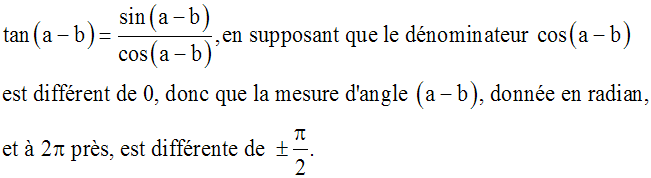
J’obtiens :

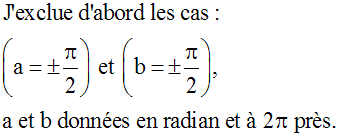
Ainsi, la quantité (cosa . cosb) est différente de 0 et je peux diviser les deux membres de la fraction ci-dessus par (cosa . cosb) ; j’obtiens :
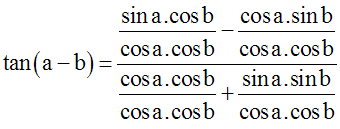
En simplifiant par cosb et cosa, j’obtiens :

J’applique les résultats à l’exercice qui suit :
On te donne une droite (d) d'équation y = 2x + 1 dans un repère orthonormal.
On te demande de trouver l'équation de la droite (d') rencontrant (d) au point A d'abscisse +1 et faisant avec (d) un angle de 30° dans le sens positif (sens contraire des aiguilles d'une montre)
Solution
On note a la mesure, donnée en radian, de l’angle orienté (d , d’), positif.
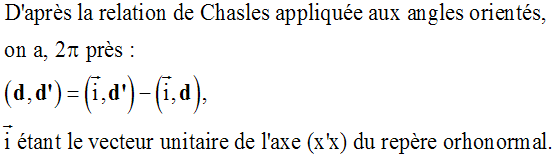
En posant z = mes (i , d’) et m = mes (i , d), on obtient :
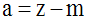
Par ailleurs, on sait que la tangente de m et celle de z sont respectivement les pentes ou coefficients directeurs des droites (d) et (d’).
En appliquant une des formules démontrées précédemment, on écrit :
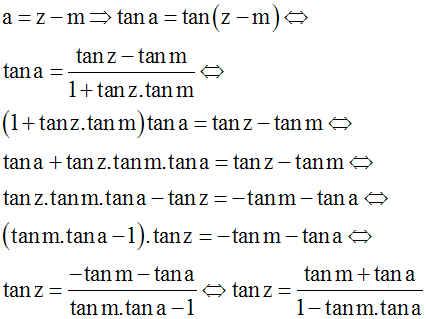

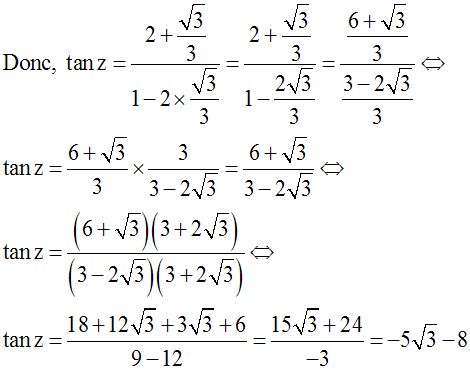
L’équation de (d’) s’écrit alors :
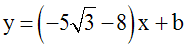
Or, (d’) rencontre (d) au point A.
Les coordonnées de A vérifient l’équation de (d) ; on a donc :
yA = 2 xA + 1 = 2.(+1) + 1 = +3
Les coordonnées de A devant vérifier l’équation de (d’), on a :
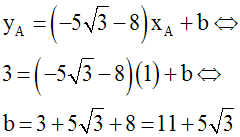
L’équation de (d’) est finalement :