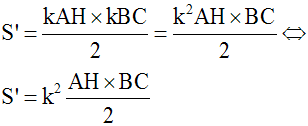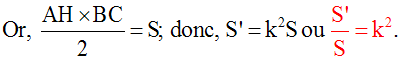GESTION DE MATHS FLASH (6)
Orthogonalité de deux vecteurs - Première partie
1- Ce que je dois connaître
Notation d’un vecteur (Rappels)

Il existe au moins un couple et un seul de nombres réels (X , Y) tel que :
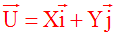
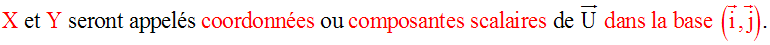

Exemple :
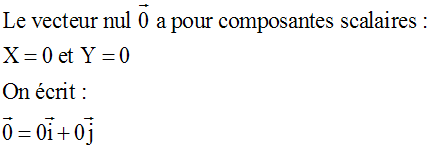
Tout
vecteur dont X est différent de 0 et Y est nulle a
son support ou sa direction parallèle à l’axe des
abscisses.
Tout vecteur dont Y est différent de 0 et X est nulle a son support ou sa direction parallèle à l’axe des ordonnées.
Egalité de deux vecteurs
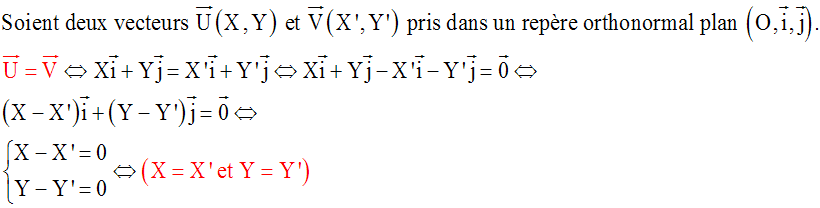
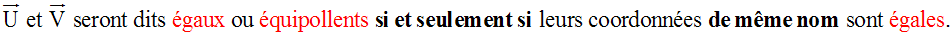
Propriétés
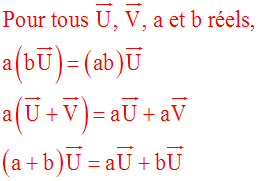
Module d’un vecteur

On a :
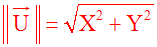


Orthogonalité de deux vecteurs

En Seconde, on admettra ce théorème sans démonstration.
Exemple :

Conséquence
Dans un repère orthonormal, deux droites (d) et (d')
d'équations réduites respectives y = ax + b et
y = a'x + b', avec a et a' nombres réels différents de 0, sont
orthogonales si et
seulement si a . a' = –1.
Démonstration

2- Je m’entraîne
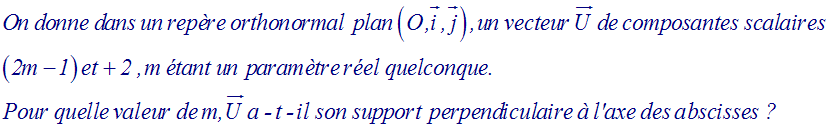
Solution


Solution

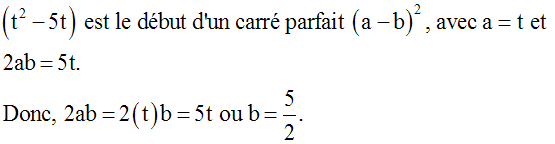
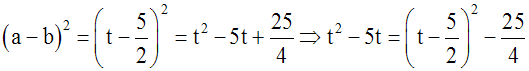
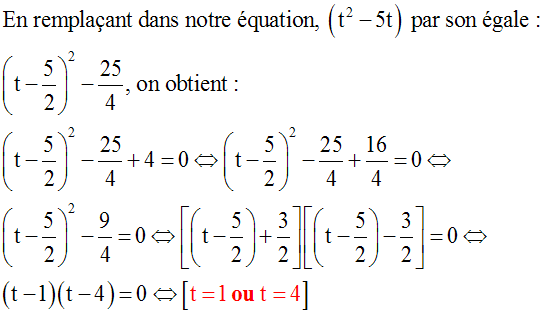
Conclusion



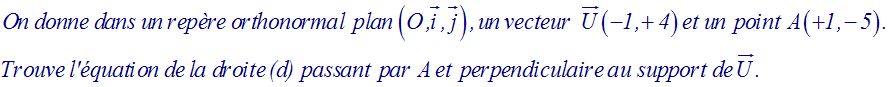
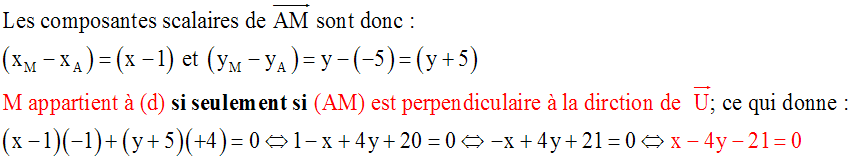
L’équation de (d) est
donc :
x – 4y – 21 = 0

Solution


Application
(d) : 2x + 3y – 5 = 0, avec u = +2 et v = +3


Solution


Solution


Solution
xO + 5yO – 1 = (0) + 5(0) – 1 = –1, différent de 0 ; le coordonnées de O ne vérifiant pas l’équation de (d), O n’appartient pas à (d).
Soit (D) la perpendiculaire à (d), abaissée de O. Soit H l’intersection de (D) et (d).
Par définition, OH sera la distance de O à (d).
Pour calculer OH, il suffit de trouver les coordonnées de H puis d’appliquer la formule donnant OH2.
Trouvons d’abord l’équation de (D).


L’équation de (D) est donc :
5x – y = 0
Trouvons les coordonnées de H.
H étant l’intersection de (d) et (D), ses coordonnées xH et yH doivent vérifier simultanément l’équation de (d) et celle de (D).
Donc on devra avoir le système :
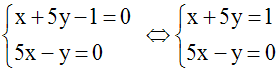
Le déterminant de Cramer est :

Ce déterminant étant différent de 0, le système admet une solution
unique (x0 , y0) telle que x0 et y0 réels.

Donc, les coordonnées de H sont :
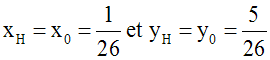
Calcul de la distance OH.
On a :
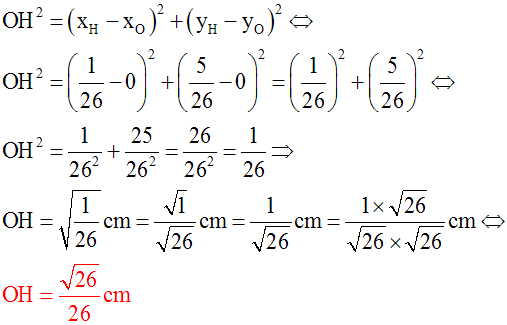

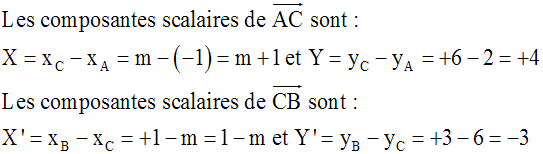

Or, (m2 + 11) est strictement positive quelle que soit la valeur donnée au paramètre réel m.
Donc, il n’existe aucun réel m tel que XX' + YY' = 0 ou encore tel que (AC) est orthogonale à (CB).
Orthogonalité de deux vecteurs - Deuxième partie

Solution
Pour que les points A, B et C soient trois des sommets d’un carré de côté AB il suffit que l’on ait :


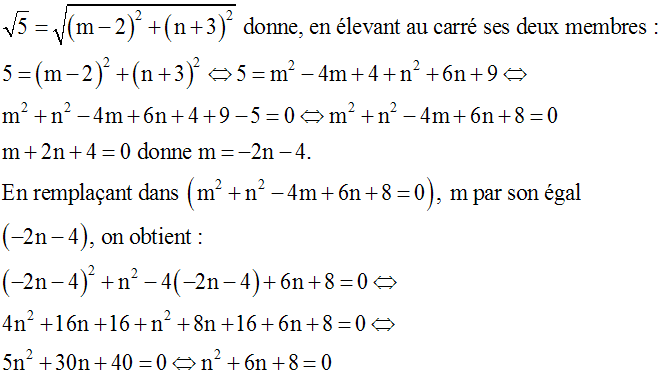
On devra donc résoudre cette dernière équation.
n2 + 6n est le début du carré parfait (a + b)2, ave a = n et 2ab = 6n.
Ceci donne a = n et ab = 3n ; donc a = n et b = 3.
Ainsi, (n + 3)2 = n2 + 6n + 9 donne n2 + 6n = (n + 3)2 – 9.
En remplaçant dans l’équation (n2 + 6n + 8 = 0), (n2 + 6n) par son égale (n + 3)2 – 9, on obtient :
(n + 3)2 – 9 + 8 = 0 ou (n + 3)2 – 1 = 0
On reconnaît la forme A2 – B2 du premier membre ; donc :
[(n + 3) + 1][(n + 3) – 1] = 0 ou
(n + 4)(n + 2) = 0 ou
(n = – 4 ou n = – 2)
Pour n = – 4, m = –2n – 4 = – 2(– 4) – 4 = + 8 – 4 = + 4.
Pour n = – 2, m = –2n – 4 = – 2(– 2) – 4 = + 4 – 4 = 0.
Conclusion :
Pour que les points A, B et C soient trois des sommets d’un carré de côté [AB] il suffit que l’on ait :
(m = + 4 et n = – 4) ou (m = 0 et n = – 2)
Médiatrice d’un segment
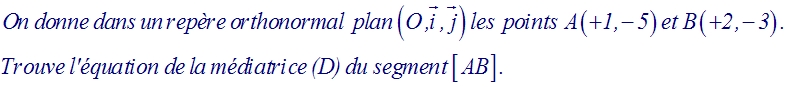
Solution
La médiatrice (D) de [AB] est orthogonale à (AB) et contient le milieu M de [AB].
On sait que :
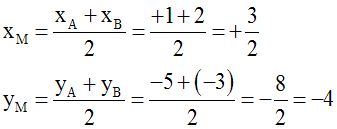
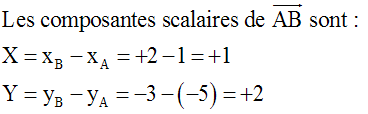
Soit P(x , y) un point quelconque du repère.
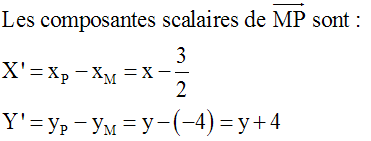

L’équation de (D) est donc :
2x + 4y + 13 = 0

Solution

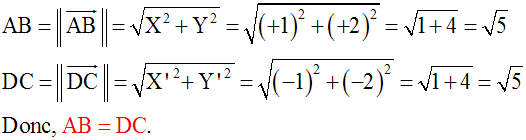
(ABDC) ayant deux côtés opposés, [AB] et [DC], parallèles et de même longueur, est un parallélogramme.
Orthogonalité de deux vecteurs - Troisième partie
Symétries centrale et axiale
1-
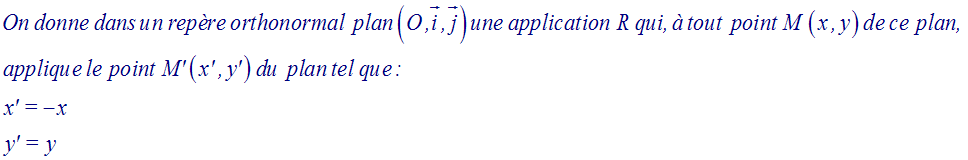
Donne la nature de R.
Pour la suite on notera R par S(y’y).
2-
Explicite S(x’x).
3-
On pose SO la symétrie centrale de centre l’origine O du repère.
Donne les équations qui explicitent SO.
4-
On donne la droite (d)
d’équation : 2x + 3y + 1 = 0.
Détermine l’équation de (I), symétrique de la droite (d), dans SO.
Détermine l’équation de (J), symétrique de la droite (d), dans S(x’x).
Détermine l’équation de (K), symétrique de la droite (d), dans S(y’y).
Solution1-
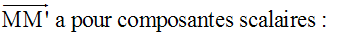
X = xM’ – xM = x’ – x = (–x) – x = –2x
Y = yM’ – yM = y’ – y = y – y = 0

(–2x)(0) + (0)(+1) = 0 ; donc (MM’) est orthogonale au support de j, donc à (y’Oy).
Soit W milieu de [MM’].
On sait que :
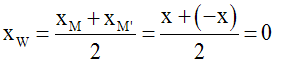
W ayant ainsi une abscisse nulle, appartient à l’axe des ordonnées (y’Oy).
Par conséquent (y’Oy) coupe [MM’] en son milieu W.
Conclusion :
(MM’) étant orthogonale à (y’Oy) et (y’Oy) coupant [MM’] en son milieu W, (y’Oy) est médiatrice de [MM’] et R est la symétrie axiale d’axe (y’Oy).
Pour la suite, R sera notée S(y’y).
2-
S(x’x) sera la symétrie axiale d’axe (x’Ox).
A tout point M(x , y) elle applique le point M’(x’ = x et y’ = –y).
3-
La symétrie centrale, SO, de centre O, origine du repère, applique à tout point M(x , y), le point
M’(x’ = –x et y’ = –y).
4-
On donne la droite (d) d’équation : 2x + 3y + 1 = 0.
Pour tout point M(x , y) appartenant à (d), son image par SO est le point M’(x’ , y’) tel que
x’ = –x et y’ = –y.
Donc x = –x’ et y = –y’.
En remplaçant dans l’équation 2x + 3y + 1 = 0, x et y par leurs égales –x’ et –y’, on obtient :
2(–x’) + 3(–y’) + 1 = 0 ou –2x’ – 3y’ + 1 = 0 ou
2x’+ 3y’ – 1 = 0
L’équation de (I), symétrique de la droite (d) dans SO, est donc :
2x + 3y – 1 = 0.
Pour tout point M(x , y) appartenant à (d), son image par S(x’x) est le point M’(x’ , y’) tel que
x’ = x et y’ = –y.
Donc x = x’ et y = –y’.
En remplaçant dans l’équation 2x + 3y + 1 = 0, x et y par leurs égales x’ et –y’, on obtient :
2(x’) + 3(–y’) + 1 = 0 ou 2x’ – 3y’ + 1 = 0
L’équation de (J), symétrique de la droite (d) dans S(x’x), est donc : 2x – 3y + 1 = 0.
Pour tout point
M(x , y) appartenant à (d), son image par S(y’y)
est le point M’(x’ , y’) tel que
x’ = –x et y’ = y.
Donc x = –x’ et y = y’.
En remplaçant dans l’équation 2x + 3y + 1 = 0, x et y par leurs égales –x’ et y’, on obtient :
2(–x’) + 3(y’) + 1 = 0 ou –2x’ + 3y’ + 1 = 0 ou 2x’ – 3y’ – 1 = 0
L’équation de (K), symétrique de la droite (d) dans S(y’y), est donc : 2x – 3y – 1 = 0.
Fonctions numériques (généralités)
Rappels et définitions
On donne deux ensembles quelconques E
et F. Les objets qui les constituent sont appelés
éléments.
Une relation
f de E vers
F est une correspondance liant des éléments de E à des
éléments de F.
E sera appelé
ensemble de départ ou
source et
F, ensemble
d'arrivée ou
but.
Si l'élément x de E est lié, par f, à un élément y de F,
alors on dira que y est
l'image de
x par f; quant à x, il sera
l'antécédent
de y par f.
La partie de F composée de tous les éléments qui sont images
d'éléments de E par f sera notée
Imf.
Une relation f de E vers F sera dite
application
de E
dans F si et
seulement si
tout élément de la
source E possède par f
une image et une seule
dans le but F.
Ainsi, il suffit qu'i y ait
un élément de E
ne possédant aucune image
par f dans F pour que f ne soit pas
une application.
Comme
aussi il suffit qu'il y ait
un élément de E
possédant plus d'une
image par f dans F pour que f ne soit pas
une application.
Dans le cas particulier où E = F, alors on dira que f est
une application dans
E ou dans F.
Une fonction réelle
d'une variable réelle, notée f, est
une application
d'une partie E de
R dans R.
Ici, R est l'ensemble de nombres réels.
La partie E de R
sera appelée domaine
de définition de f et
notée Dom(f).
Souvent une fonction réelle d'une variable réelle sera
simplement appelée
fonction numérique.
Si x est un élément de Dom(f) et y son image par f dans R,
alors on écrira :
y = f(x)
qui se lira :" y est
l'image de x par f
".
Exemples :
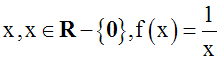
a pour domaine de définition Dom(f) =
R – {0}.
On remarque que l'élément 0 n'a aucune image par f puisque
l'inverse de 0 n'existe pas.
La fonction réelle g de la variable réelle t définie par :
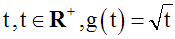
a pour domaine de définition Dom(g) =
R+.
(ici,
R+ désigne
l'ensemble des nombres
réels positifs)
On remarque que tout réel strictement négatif n'a aucune
image par g puisque dans
R la racine carrée d'un nombre strictement
négatif n'existe pas.
Soit f une fonction réelle de
la variable réelle x et soit Dom(f) son domaine de
définition.
1-
On dira que f est largement croissante sur Dom(f) si et seulement si :

Cette implication logique peut également s'écrire :
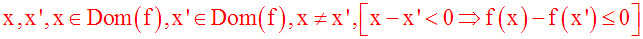
ou encore,
puisque x et x' sont différents, c'est-à-dire (x – x')
différent de 0,
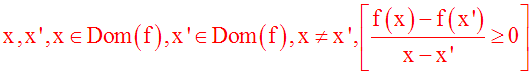
On dira que f est strictement croissante sur Dom(f) si et seulement si :

Cette implication logique peut également s'écrire :

ou encore,
puisque x et x' sont différents, c'est-à-dire (x – x')
différent de 0,
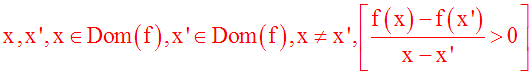
3-
On dira que f est
largement décroissante sur Dom(f)
si et seulement si :
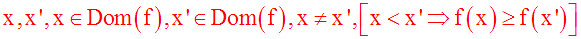
Cette implication logique peut également s'écrire :
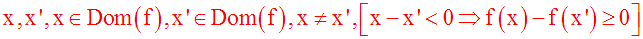
ou encore,
puisque x et x' sont différents, c'est-à-dire (x – x')
différent de 0,
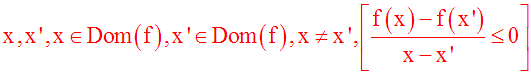
4-
On dira que f est strictement
décroissante sur Dom(f) si
et seulement si
:

Cette implication logique peut également s'écrire :
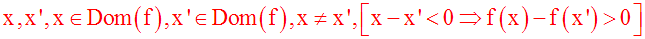
ou encore,
puisque x et x' sont différents, c'est-à-dire (x – x')
différent de 0,
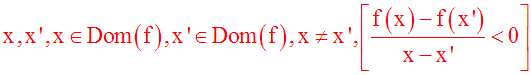
5-
On dira que f est constante sur
Dom(f) si et seulement si
:
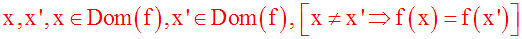
Cette implication logique peut également s'écrire :
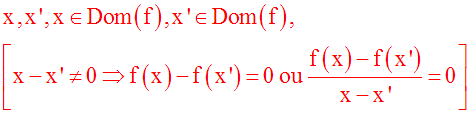
Une fonction réelle d'une variable
réelle sera dite
monotone au sens large
sur son domaine de définition si et seulement si elle
est largement
croissante ou largement décroissante
sur ce domaine.
Elle sera dite
strictement monotone
sur son domaine de définition si et seulement si elle
est strictement
croissante ou strictement décroissante
sur ce domaine.
Conclusion
Pour
démontrer qu'une fonction réelle d'une variable réelle est
strictement croissante
(resp. largement
croissante) sur son domaine de
définition, il suffit de démontrer que le rapport :
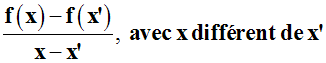
est
strictement positif
(resp.
largement positif)
sur ce domaine.
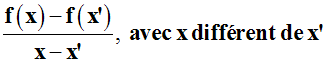
est
strictement négatif
(resp.
largement négatif)
sur ce domaine.
Pour démontrer qu'une fonction réelle d'une variable réelle
est constante
sur son domaine de définition, il suffit de démontrer que le
rapport :
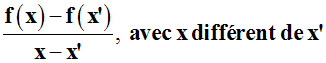
est nul
sur ce domaine.
Exercices
1-
On donne la fonction numérique f définie par :

On demande d'expliciter son domaine de définition.
Solution
Le dénominateur
ne pouvant s'annuler
et la racine carrée d'un nombre réel
négatif n'existant pas,
le domaine de définition de f est l'ensemble des nombres
réels strictement positifs, noté
R*+.
Ainsi Dom(f)
= R*+
2-
On donne la fonction numérique g définie par :
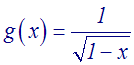
On demande d'expliciter son domaine de définition.
Solution
Pour les mêmes raisons que ci-dessus, le domaine de définition de g est l'ensemble des nombres réels x tels que : 1 – x > 0
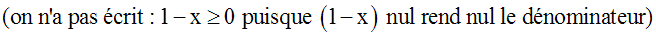
La résolution de cette inéquation en x donne x < 1.
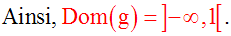
On remarque que les " dents
" des crochets sont
dirigées vers l'extérieur de l'intervalle,
ceci pour préciser que la valeur 1 et moins l'infini sont
des valeurs exclues
du domaine de définition
de g.
On donne la fonction numérique h définie par :
h(t) = t2
On demande d'expliciter son domaine de définition et d'étudier ses variations sur ce domaine.
Solution
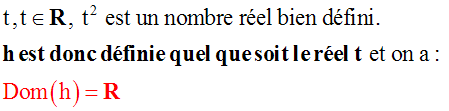
Soient t et t'
deux réels différents, quelconques. On a donc (t –
t') différent de 0.
Formons le rapport :
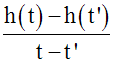
On écrit :

(t – t')
étant non nul, on peut simplifier par (t – t').
On obtient :
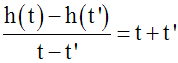
Ainsi, on a les résultats suivants :
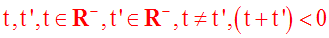
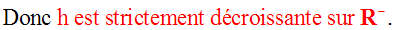
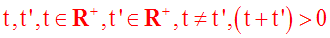

(ici, R-
désigne l'ensemble des nombres réels largement négatifs et
R+ ceux
largement positifs)
4-
On donne la fonction numérique U définie par :
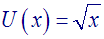
On demande d'expliciter son
domaine de définition et d'étudier ses variations sur ce
domaine.
Solution
La racine carrée d'un nombre réel strictement négatif n'existant pas, U n'est définie que pour les réels largement positifs; donc :

Soient x et x' deux réels
différents, quelconques, appartenant à R+.
On a donc (x – x') différent de 0.
Formons le rapport :
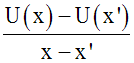
On écrit :
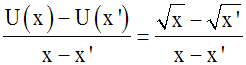
(x – x') étant
différent de 0, multiplions le numérateur et le
dénominateur de cette dernière expression par le conjugué de
l'expression :
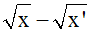
On écrit :
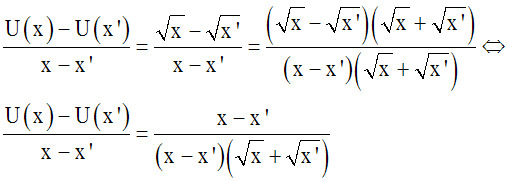
On obtient :
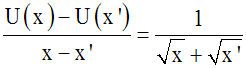
Ainsi,
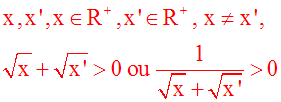
Donc
U est strictement croissante sur R+.
Les mesures dans deux triangles
semblables Rappel 2-
La même démonstration sera
utilisée pour les autre hauteurs homologues. Nous
dirons que dans deux
triangles semblables, les longueurs de deux hauteurs
homologues sont dans un rapport égal au rapport de
similitude.
Démonstration
Comme (ABC) et
(A'B'C') sont semblables, nous avons :
Démonstration
P '= A'B' + B'C' +
A'C' Or, (ABC) et (A'B'C')
étant semblables, nous avons :
D'après une propriété
des proportions, nous pouvons en déduire que :
1-
NB :
Les troisèmes angles le seront également puisque la
somme des angles intérieurs est une constante égale
à un plat (180°).
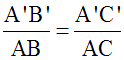
Les longueurs de leurs côtés sont respectivement
proportionnelles :
Ainsi, pour démontrer
que deux triangles ont même
forme ou sont
semblables, il
suffit de démontrer qu'ils vérifient
un quelconque
de ces trois cas de similitude.
1-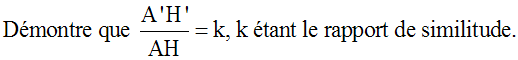
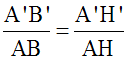
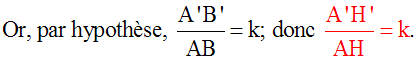
2-
Dans le triangle (ABC), soit [AM] la médiane
relative au côté [BC]; M est donc milieu de [BC].
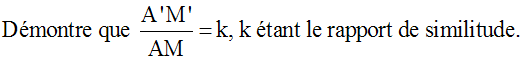
Il en sera de même pour les autres médianes
homologues.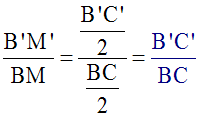
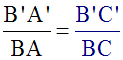
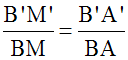
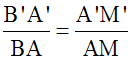
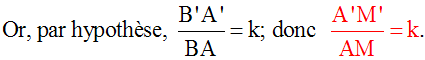
Nous
dirons que
dans deux triangles semblables, les
longueurs de deux médianes homologues sont sont dans
un rapport égal au rapport de
similitude.
3-
Soient P et P' respectivement les périmètres de (ABC) et
de (A'B'C').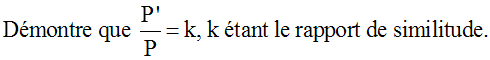
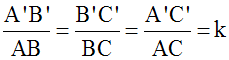
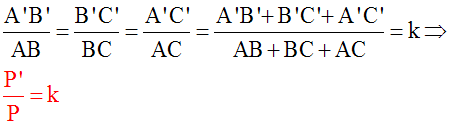
Soient S et S' respectivement les aires des surfaces de (ABC) et de (A'B'C').
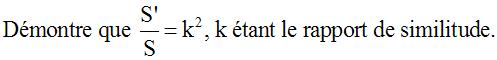
Démonstration
Soient [AH] la hauteur relative au côté [BC], dans (ABC) et [A'H'] la hauteur relative au côté [B'C'], dans (A'B'C'). [AH] et [A'H'] sont homologues dans les triangles semblables (ABC) et (A'B'C').
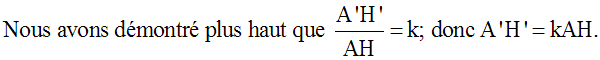
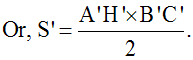
Remplaçons dans cette formule A'H' par son égale k.AH et B'C' par son égale k.BC; nous obtenons :