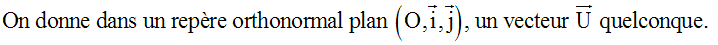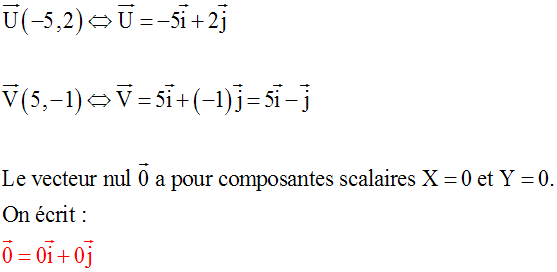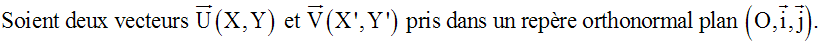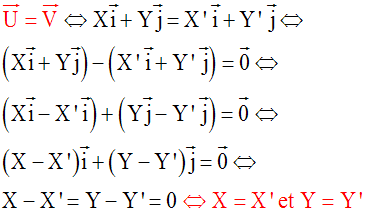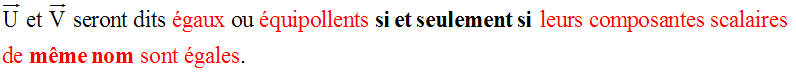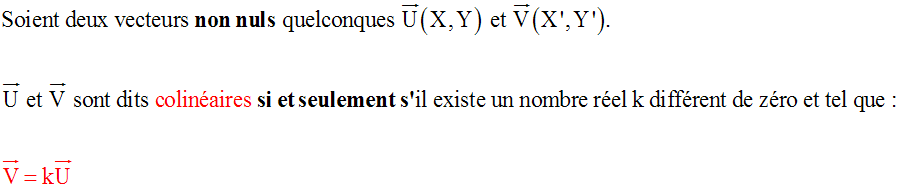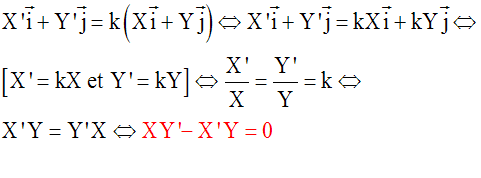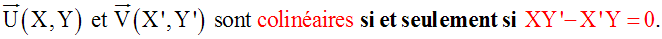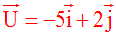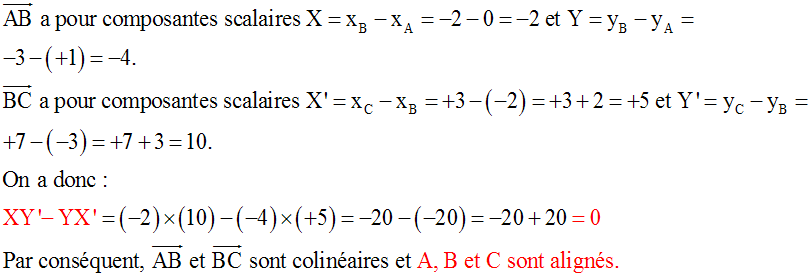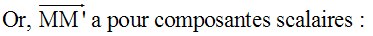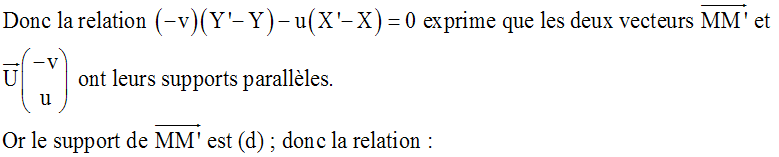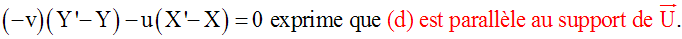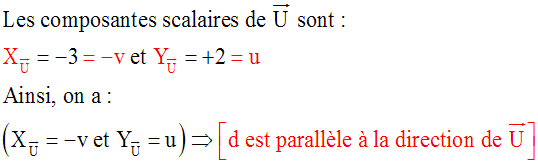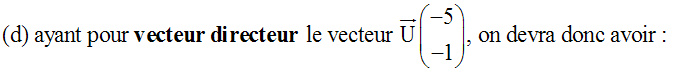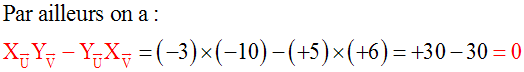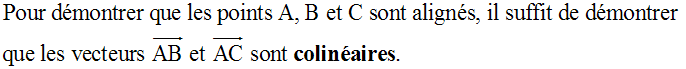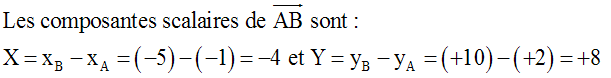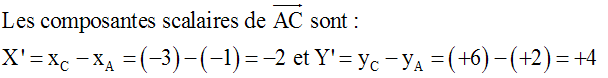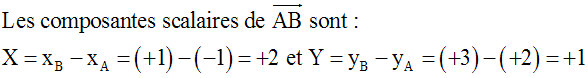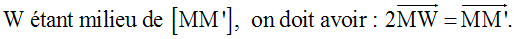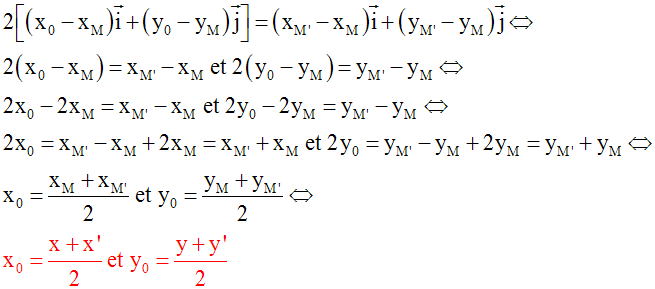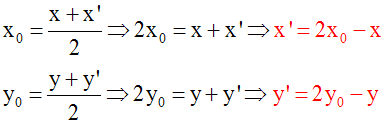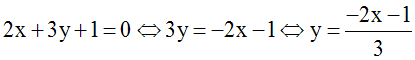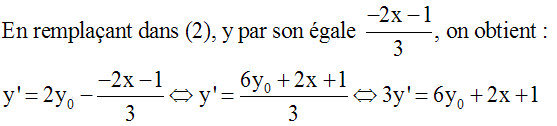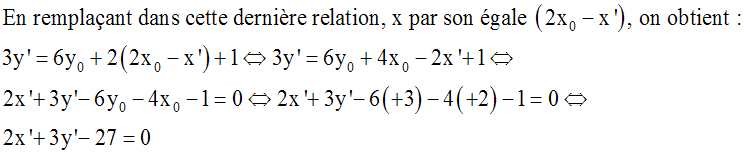Colinéarité des vecteurs - Deuxième partie


Solution
Soient M(X , Y) et M’(X’ , Y’) deux
points quelconques de (d).
Leurs coordonnées
doivent donc vérifier
l’équation de (d) et on a :
uX + vY + w = 0
uX’ + vY’ + w = 0
En soustrayant membre à membre, on
obtient :
u(X – X’) + v(Y – Y’) = 0 ou (–u)(X’ –
X) – v(Y’– Y) = 0 ou
(–v)(Y’– Y) – u(X’–X) = 0
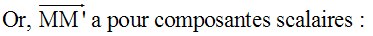
(X’ – X) et (Y’ – Y)
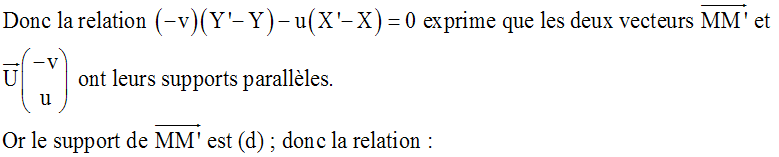
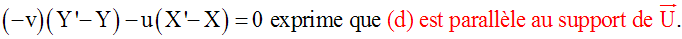

(–v)(Y – Y0) – u(X – X0)
= 0 ou –vY + vY0 – uX + u X0
= 0 ou
–uX – vY + (vY0 + uX0)
= 0 ou
uX + vY – (vY0 + uX0)
= 0, ou
uX + vY + w
= 0, avec w = – (vY0 + uX0)
Application
(d) : 2x + 3y – 5 = 0, avec u = +2 et v
= +3
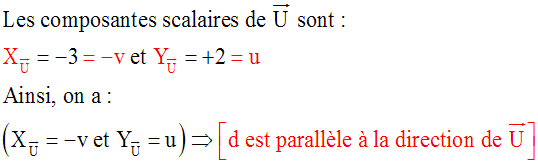


Solution
L’équation de (d) est de la forme ux +
vy + w = 0.
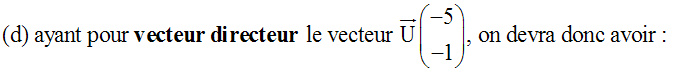
–v = –5 et u = –1 ou v = +5 et u = –1.
L’équation de (d) est donc :
(–1)x +
(+5)y + w = 0 ou
–x + 5y + w = 0
Or, A appartient à (d) ; donc, les
coordonnées de A doivent vérifier
l’équation de (d) et on a :
– xA + 5yA + w = 0
ou –(+2) + 5(–3) + w = 0 ou – 2 – 15 =
– w
ou
w = + 17
L’équation de (d)
est donc :
–x + 5y + 17 = 0
ou x –
5y – 17 = 0

5x + 3y
– 5 = 0 et –10x – 6y + 13 = 0
Démontre que (d) et (d’) sont
parallèles.
Solution

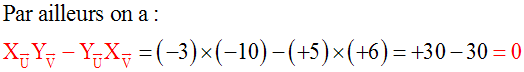
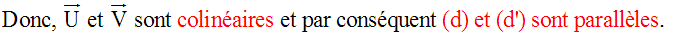

A (–1 ,
+2), B(–5 , +10) et C(–3 , +6).
Démontre que ces points sont alignés.
Solution
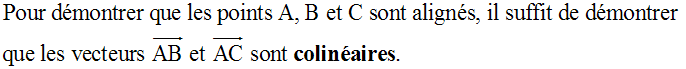
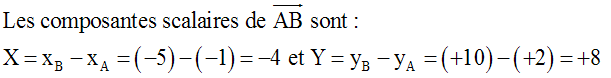
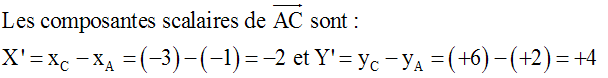
Donc,
XY’ – YX’
= (–4)(+4) – (+8)( –2) = –16 + 16
= 0.
Donc,
A, B et C sont
alignés.

A (–1 ,
+2), B(+1 , +3) et C(m , +6) ; m étant
un paramètre réel non nul.
Pour
quelle valeur de m, les points A, B et C
sont alignés ?
Solution
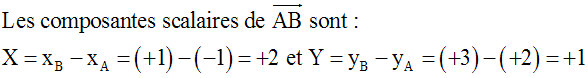
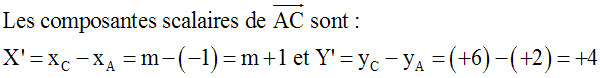
Pour que A, B et C soient alignés,
il suffit que :
XY’ – YX’ = 0 ou (+2)(+4) – (+1)(m+1) =
0 ou +8 – m – 1 = 0
ou
m
= +8 – 1
= +7
Milieu
d’un segment et symétrie centrale
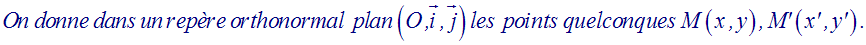
1-
Calcule
les coordonnées du point W (x0
, y0), milieu du segment
[MM’].
2-
Exprime
x’ et y’ en fonction de x0, y0,
x et y.
3-
On
donne la droite (d) d’équation : 2x + 3y
+ 1 = 0 et le point W (+2 ,
+3).
Détermine l’équation de (I), symétrique
de (d) dans la symétrie centrale W.
Solution
1-
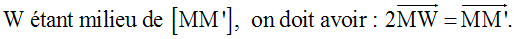
Cette égalité vectorielle peut encore
s’écrire :
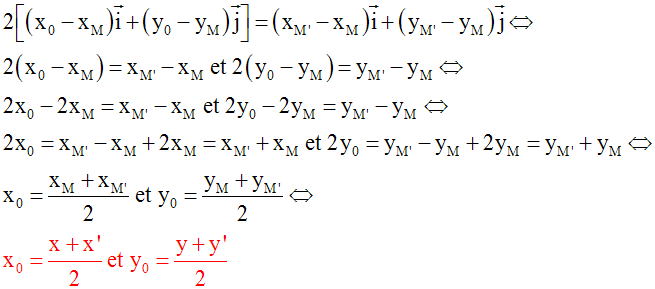
Les coordonnées du milieu d’un segment
sont égales aux demi sommes des
coordonnées de
ses extrémités.
2-
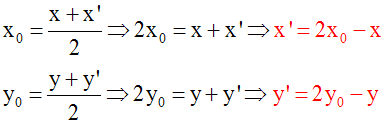
3-
Soit un point M (x , y) quelconque de
la droite (d).
Son symétrique M’(x’ , y’) dans la
symétrie centrale de centre
W(x0 , y0) doit,
selon le résultat
obtenu à la question
(2) ci-dessus, avoir ses coordonnées x’
et y’ vérifier les deux relations :
x’ = 2x0 – x (1)
y’ = 2y0 – y (2)
ou
x = 2x0 – x’
y = 2y0 – y’
L’image (I) de (d) par cette symétrie
sera donc l’ensemble des points M’(x’ ,
y’) ; pour expliciter (I),
il suffit
de trouver une relation liant x’ et y’.
Les cordonnées de M vérifient l’équation
de (d) ; donc :
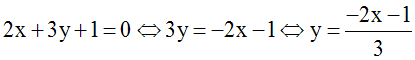
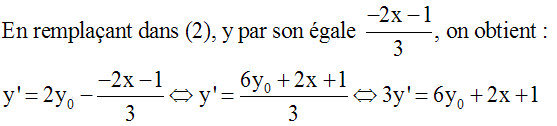
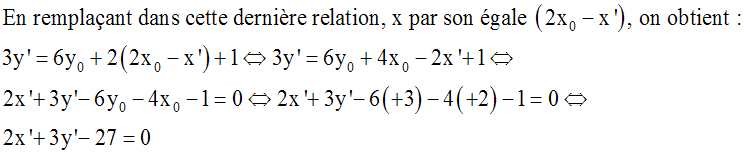
(I) est donc la droite 2x + 3y – 27 = 0.
On remarque que (I) est parallèle à
(d) ; il fallait s’y attendre car
la
symétrie centrale conserve le
parallélisme.