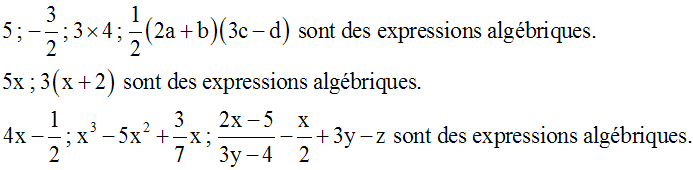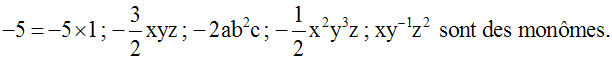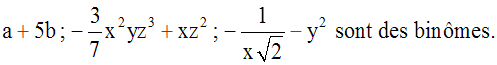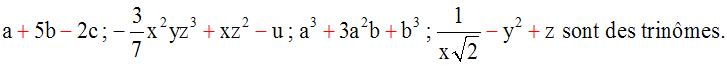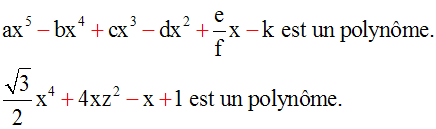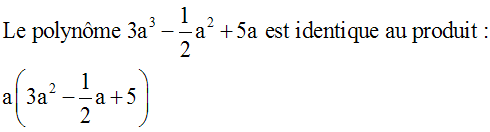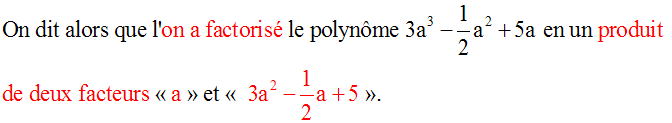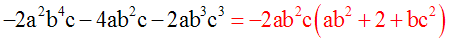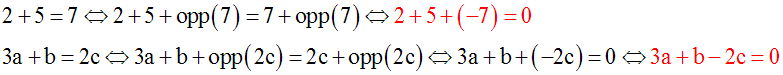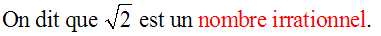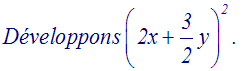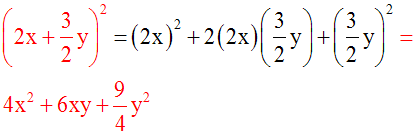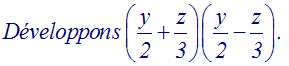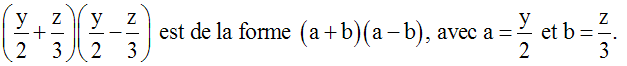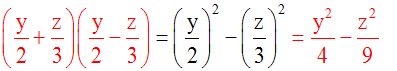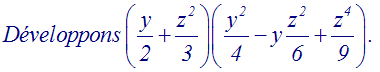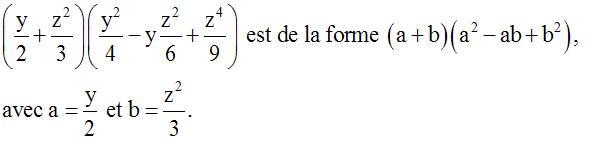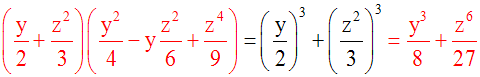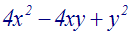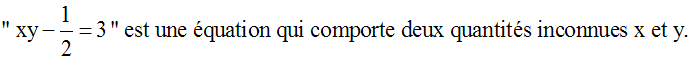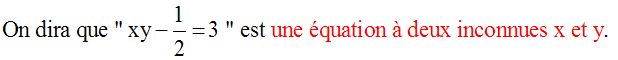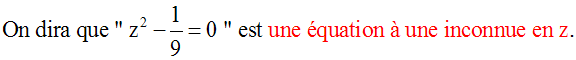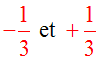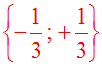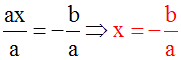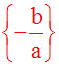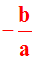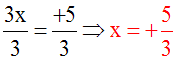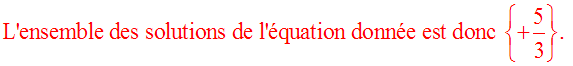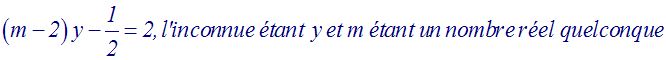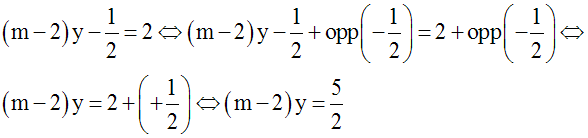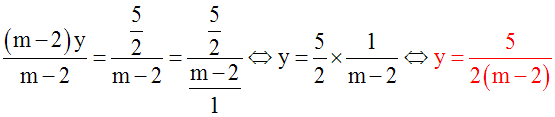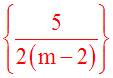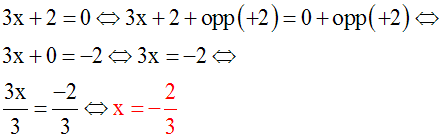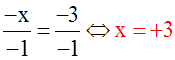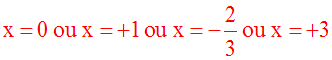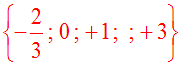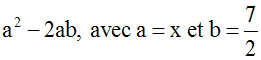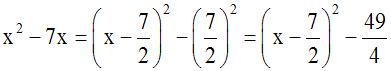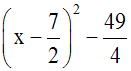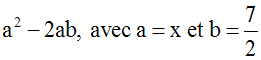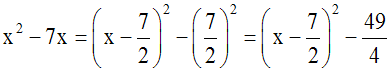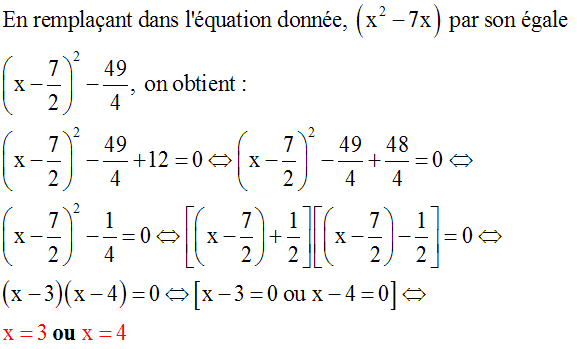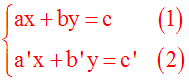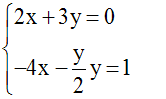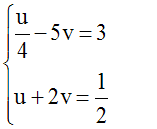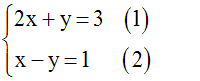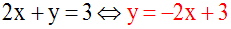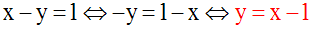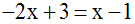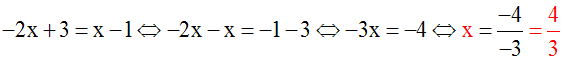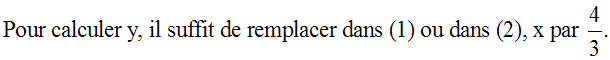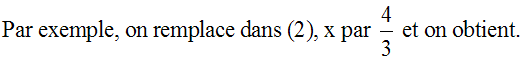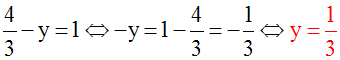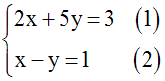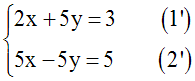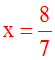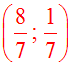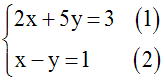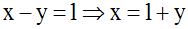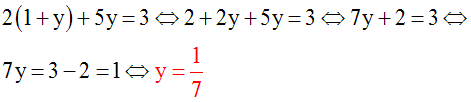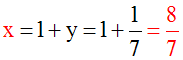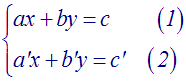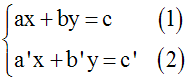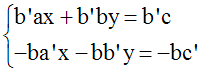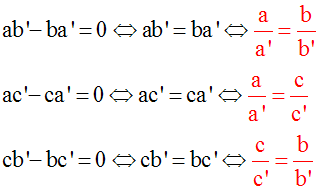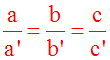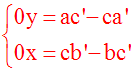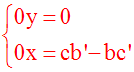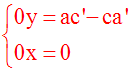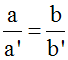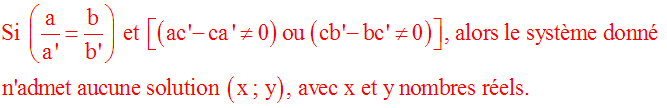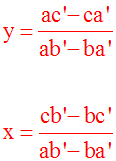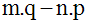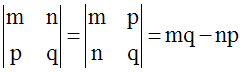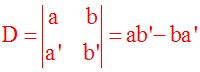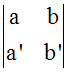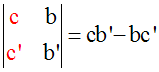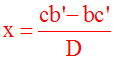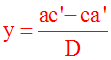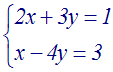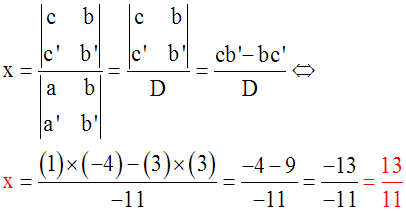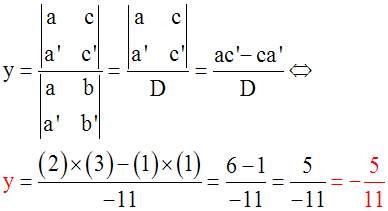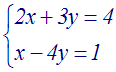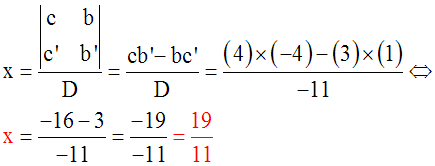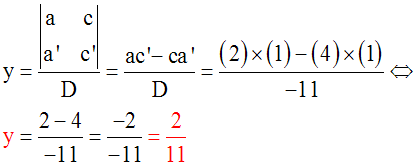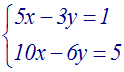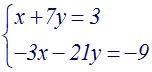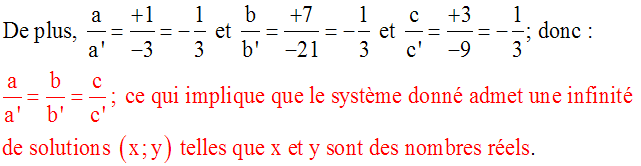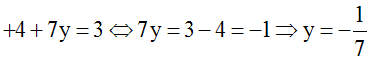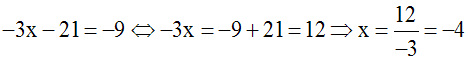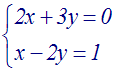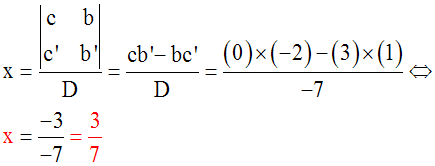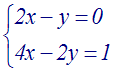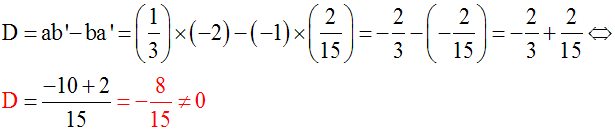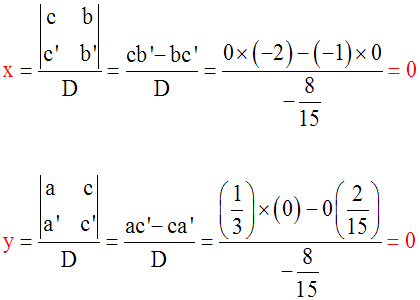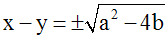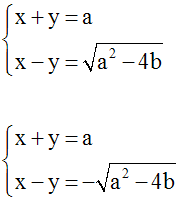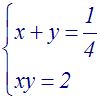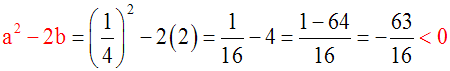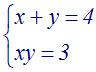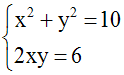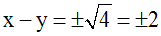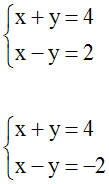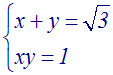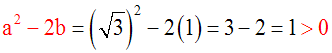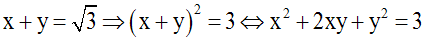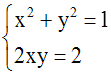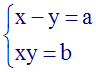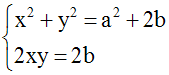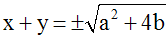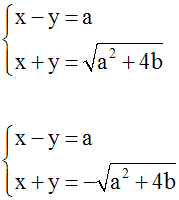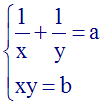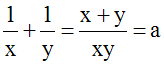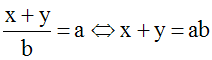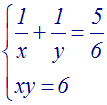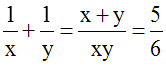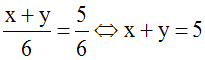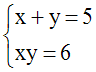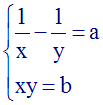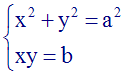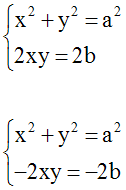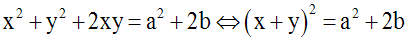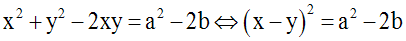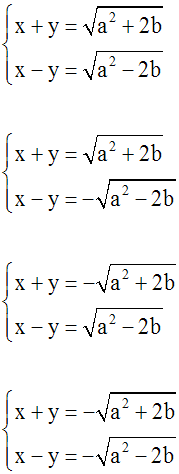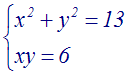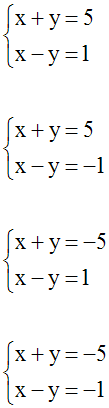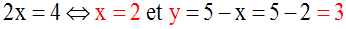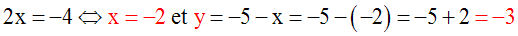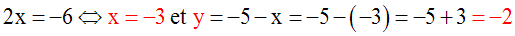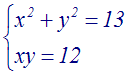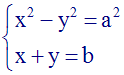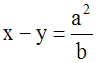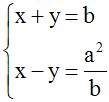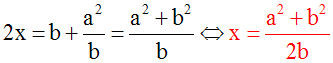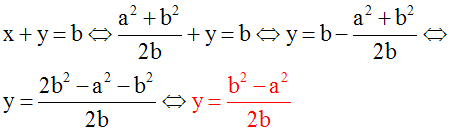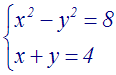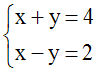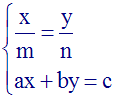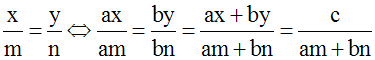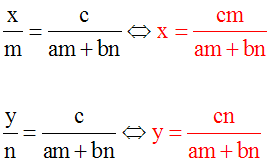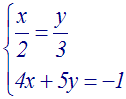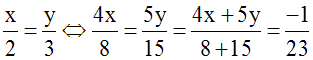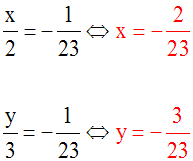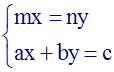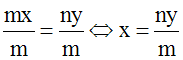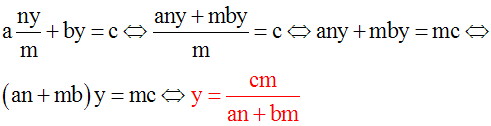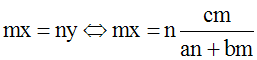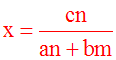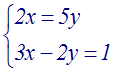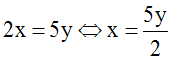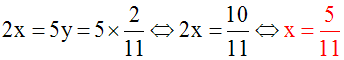Identités remarquables - équations - systèmes
d'équations - Troisième partie
3-6- Identités remarquables dans
l’ensemble des nombres réels
Un nombre
réel
est un nombre
rationnel
ou
irrationnel.
L’ensemble
des nombres rationnels et des nombres
irrationnels est appelé
ensemble des
nombres réels.
Les sept identités
remarquables ci-dessus, vraies dans
l’ensemble des nombres rationnels,
sont également
vraies dans l’ensemble des nombres réels.
On a donc :
(a + b)2
= a2
+ 2ab + b2
(a – b)2
=
a2
– 2ab + b2
(a + b)3
= a3
+ 3a2b
+ 3ab2
+ b3
(a – b)3
=
a3
– 3a2b
+ 3ab2
– b3
(a + b)(a – b)
=
a2
– b2
a3
+ b3
=
(a + b)(a2
– ab + b2)
a3
– b3
= (a – b)(a2
+ ab + b2)
Les démonstrations sont les mêmes que celles
développées dans la deuxième partie de ce
cours.
3-7- Applications immédiates des
identités remarquables
Les identités
remarquables servent à
développer
des produits de facteurs
Exemples :
Développons (2x – 5)2.
(2x – 5)2 est de la forme (a – b)2,
avec a = 2x et b = 5.
Nous pouvons donc appliquer l’identité
remarquable :
(a – b)2
=
a2
– 2ab + b2
(2x – 5)2
= (2x)2 – 2(2x)(5) + 52
= 4x2
– 20x + 25.
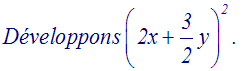

Nous pouvons donc appliquer l’identité
remarquable :
(a + b)2
= a2
+ 2ab + b2
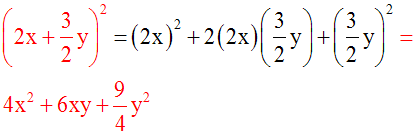
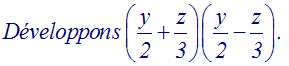
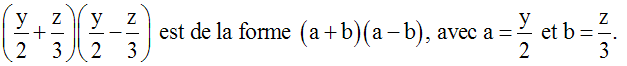
Nous pouvons donc appliquer l’identité
remarquable :
(a + b)(a – b) = a2
– b2
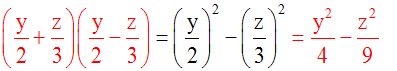
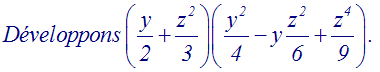
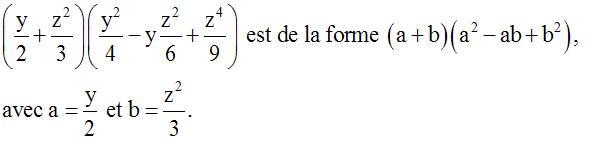
Nous pouvons donc appliquer l’identité
remarquable :
(a + b)(a2
– ab + b2)
= a3
+ b3
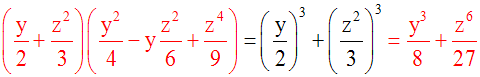
Les identités
remarquables servent à
factoriser
des expressions algébriques
Exemples :
Factorisons l’expression :
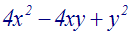
Cette expression est de la forme a2
– 2ab + b2, avec a = 2x et b = y.
Or, a2 – 2ab + b2 est
identique à (a – b)2.
Nous pouvons donc
écrire :
4x2
– 4xy + y2 = (2x – y)2
Factorisons l’expression :
16x2 – y2
Cette expression est de la forme a2
– b2, avec a = 4x et b = y.
Or, a2 – b2 est
identique à (a + b)(a – b).
Nous pouvons donc
écrire :
16x2
– y2 = (4x + y)(4x – y)
Factorisons l’expression :
27a3 + b3
Cette expression est de la forme x3
+ y3, avec x = 3a et y = b.
Or, x3 + y3 est
identique à (x + y)(x2 – xy + y2).
Nous pouvons donc écrire :
27a3 + b3
= (3a + b)(9a2 – 3ab + b2)
Factorisons l’expression :
25x2 – 30xy – 40y2
Nous constatons d’abord que l’expression 25x2
– 30xy peut se mettre sous la forme :
a2 – 2ab, avec a = 5x et b = 3y.
Or, (a – b)2
= a2
– 2ab + b2
implique a2
– 2ab =
(a – b)2
– b2.
Ainsi, 25x2 – 30xy = (5x – 3y)2
– (3y)2 = (5x – 3y)2 –
9y2.
Dans l’expression donnée, remplaçons 25x2
– 30xy par son égale
(5x – 3y)2 – 9y2.
Nous obtenons :
(5x – 3y)2 – 9y2 – 40y2
= (5x – 3y)2 – 49y2
Or, (5x – 3y)2 – 49y2
est de la forme a2 – b2,
avec a = 5x – 3y et
b = 7y.
Nous savons que a2 – b2
est identique à (a + b)(a – b).
Nous pouvons donc écrire :
(5x – 3y)2 – 49y2 =
[(5x – 3y) + 7y][(5x – 3y) – 7y] =
(5x + 4y)(5x – 10y) = 5(5x + 4y)(x – 2y)
Conclusion :
25x2
– 30xy – 40y2
= 5(5x +
4y)(x – 2y)
Identités remarquables - équations - systèmes
d'équations - Quatrième partie
4- Équations
4-1- Définitions
On appelle
équation
toute égalité comportant des quantités
inconnues
représentées généralement par des lettres.
Résoudre une équation
consiste à trouver
l’ensemble des
valeurs que peut prendre l’inconnue et pour
lesquelles l’égalité est vérifiée.
Ces valeurs sont appelées
solutions
ou racines
de l’équation.
Exemples :
« x – 5 = 0 » est une
équation qui ne comporte qu’une quantité
inconnue : x.
On dira que « x – 5 = 0 » est
une équation à une
inconnue en x.
L’ensemble des
solutions
ou des
racines de
cette équation est
{5}.
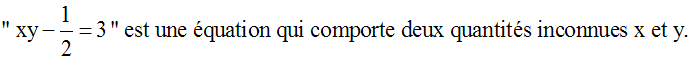
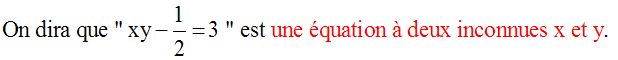

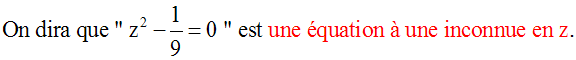
Cette équation admet
deux solutions ou
racines
dans l’ensemble des
nombres rationnels :
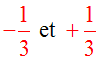
L’ensemble de ses racines se note donc :
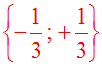
Par contre, ces
racines
n’étant pas des nombres entiers (naturels ou
relatifs), on
dira alors que cette équation
n’admet aucune
racine ou solution dans l’ensemble des
nombres entiers relatifs et dans l’ensemble
des nombres entiers naturels.
Une équation à une
inconnue est dite
du nième
degré par rapport à cette inconnue
lorsque
le plus grand
exposant
de cette inconnue dans l’expression
de cette équation est
égal à n.
Exemples :
Dans l’équation " 2x3
– 5x + 1 = 0 ", le plus grand exposant de
l’inconnue x est
3.
L’équation est donc
à une inconnue, x
et est du troisième degré par rapport à
cette inconnue.
Dans l’équation " 3y2
– 1 = 5 ", le plus grand exposant de
l’inconnue y est
2.
L’équation est donc
à une inconnue, y
et est du second degré par rapport à cette
inconnue.
Dans l’équation " t – 2 = 1 " ou encore " t1
– 2 = 1" , le plus grand exposant de
l’inconnue t est
1.
L’équation est donc
à une inconnue, t
et est du premier degré par rapport à cette
inconnue.
Dans la
suite, on se contentera d’étudier les
équations à une inconnue, du 1er
degré par rapport à cette inconnue, dans
l’ensemble des nombres réels.
Cependant, il faut savoir que cette étude
dépend aussi de l’ensemble auquel doivent
appartenir la ou les solutions ; par
exemple, résoudre une équation dans
l’ensemble des nombres entiers naturels
suppose que la propriété de divisibilité
et que l’appartenance des racines à cet
ensemble soient vérifiées.
On traitera par la suite et par des exemples
quelques cas de ce type.
Toute équation
à une inconnue, du 1er degré par
rapport à cette inconnue, peut se mettre
sous la forme générale :
ax + b = 0,
avec a et b nombres réels quelconques et x,
la quantité inconnue
Les quantités
réelles connues a et b sont appelées
coefficients de l’équation.
Exemple :
L’équation « 2z = – 7 » peut s’écrire :
2z + opp(–7) = (–7) + opp(–7)
Or, (–7) + opp(–7) =
0.
Donc 2z + opp(–7) =
2z + 7 = 0
Par abus de langage,
on dira que l’on
a fait passer le terme du second membre de
l’équation dans le premier membre, en lui
changeant son signe :
–7,
en passant
dans le premier membre, change de signe et
devient
+7.
4-2- Résolution de
l’équation à une inconnue, du 1er
degré par rapport à cette inconnue, dans
l’ensemble
des nombres réels.
1er
cas :
le coefficient a est nul
Dans ce cas, l’équation s’écrit :
0 . x + b = 0
Si b est nul,
alors l’équation se réduit à :
0 . x + 0 = 0
Quel que soit le
nombre réel x, cette dernière égalité est
vraie. On dira alors que
l’équation admet
une infinité de racines ou solutions dans
l’ensemble des nombres réels.
L’ensemble de
ses racines est l’ensemble des nombres
réels.
Si
b est différent de zéro,
alors l’équation se réduit à :
0 . x + b = 0, avec b différent de zéro
Ce qui peut s’écrire
aussi :
0 . x = – b , avec
– b différent de 0
Aucun
nombre réel ne vérifie cette égalité, puisqu’une quantité nulle (1er
membre de l’équation) ne peut à la fois être
égale à une quantité non nulle (– b).
L’équation
n’admet aucune solution dans l’ensemble des
nombres réels.
2ème
cas :
le coefficient a est différent de
zéro
Dans ce cas, l’équation s’écrit :
ax = – b
En divisant les deux membres de cette
dernière égalité par la quantité a différente de zéro, on obtient :
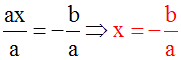
L’équation admet
une seule
racine dans l’ensemble des nombres réels.
L’ensemble de ses solutions ou racines
s’écrit alors :
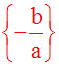
Résumé :
(a = b = 0)
implique que l’équation « ax + b = 0 » admet
une infinité de solutions dans l’ensemble
des nombres réels.
(a = 0 et b différent de 0) implique que
l’équation « ax + b = 0 » n’admet aucune
solution dans l’ensemble des nombres réels.
(a différent de
0) implique que l’équation « ax + b = 0 »
admet une seule solution :
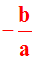
dans l’ensemble des nombres réels.
Dorénavant l’ensemble des nombres réels
sera noté R.
Exemples :
Résoudre dans
R l’équation :
3x – 5 = 0
Solution
a = 3, différent de 0 implique que
l’équation donnée admet une seule racine
dans R.
On a :
3x – 5 = 0 ou 3x – 5 + opp(– 5) = 0 + opp(–
5)
Or, – 5 + opp(– 5) = 0
Donc, 3x = 0 + opp(– 5) = 0 + 5 = + 5
En divisant les deux membres de cette
dernière équation par 3 différent de 0,
on obtient :
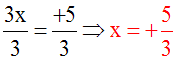
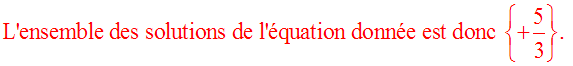
On donne
l’équation suivante :
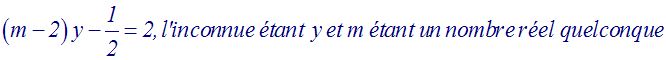
Pour quelles
valeurs de m cette équation admet-elle une
seule racine dans R ?
Trouve dans ce
cas l’ensemble de ses solutions.
Solution
Cette équation admet
une seule racine dans R pour
(m – 2)
différent de zéro ou encore pour
m différent de 2.
Dans ce cas, on peut écrire :
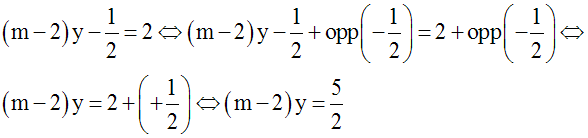
En divisant les deux membres de cette
dernière équation par (m – 2) différent
de 0, on obtient :
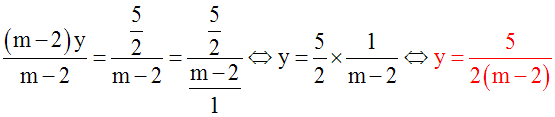
Conclusion :
Quel que soit
le nombre réel m différent de 2,
l’ensemble des solutions réelles de cette
équation est :
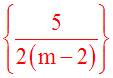
On donne dans
R l’équation suivante :
(m – 1) x + (n
+ 2) = 0, où x est l’inconnue, m et n étant
deux nombres réels quelconques.
Pour quelles
valeurs de m et de n cette équation
admet-elle une infinité de solutions dans
R ?
Solution
Cette équation admet une infinité de
solutions dans R si et seulement si :
m – 1 = 0 et n + 2 = 0
Ainsi cette
équation admet une infinité de solutions
dans R si et seulement si :
m = + 1 et n = – 2
4-3- Applications
4-3-1- Propriété
Pour qu’un
produit de plusieurs facteurs soit nul il
faut et il suffit que l’un quelconque,
au moins, de ces facteurs le soit.
On écrit
alors :
A x B x C x …..
x M = 0 si et seulement si A = 0
ou B = 0 ou C = 0 ou
….. ou M = 0
Remarque importante
Notons l’importance de
la signification du mot « ou » :
il suffit qu’au
moins un
des facteurs soit nul pour que le produit le
soit également.
Dans la rédaction de
la solution, le remplacement de ce mot par
« et »
est une
erreur grave
en mathématiques
et doit être évitée :
un énoncé de type « x
= a et
x = b, avec a
différent de b » est
faux ;
x ne peut être
simultanément
égal à a et à b différent de a.
4-3-2- Résolution d’une équation de type
A x B x C x ….. x M = 0 où chacun des
facteurs est un monôme ou binôme du premier
degré par rapport à l’inconnue
Exemples :
Résoudre dans
l’ensemble des nombres réels l’équation
suivante où x est l’inconnue :
2x(x – 1)(3x +
2)(–x + 3) = 0
Solution
Pour que ce produit
soit nul il faut et il suffit que
l’un quelconque, au
moins, de ses facteurs qui le composent soit
nul ; ainsi :
2x(x – 1)(3x + 2)( –x + 3) = 0 si et
seulement si 2x = 0 ou (x – 1) = 0 ou
(3x + 2) = 0 ou (–x + 3) = 0
Or,
2x = 0 ou x
= 0
x – 1 = 0 ou
x = + 1
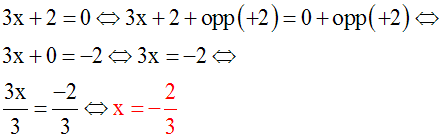
–x + 3 = 0 ou –x + 3 + opp(+ 3) = 0 + opp(+
3) ou –x = – 3 ou
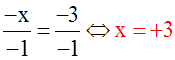
Donc, 2x(x –
1)(3x + 2)( –x + 3) = 0 si et seulement si
:
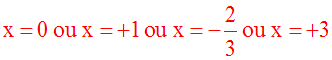
L’ensemble des
solutions dans R, de l’équation
donnée est donc :
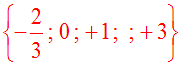
Résoudre dans
l’ensemble R l’équation suivante où x
est l’inconnue :
– 3x(x + 1)(x + 2)(x2 – 7x + 12)
= 0
Solution
Pour que ce produit
soit nul il faut et il suffit que
l’un quelconque, au
moins, de ses facteurs qui le composent soit
nul ;
ainsi :
– 3x(x + 1)(x + 2)(x2 – 7x + 12)
= 0 si et seulement si :
– 3x = 0 ou
(x + 1) = 0 ou
(x + 2) = 0 ou
(x2 – 7x + 12) = 0
Ce qui est logiquement équivalent à :
x = 0 ou x = – 1 ou x = – 2
ou (x2 – 7x + 12) = 0
Il reste à résoudre l’équation x2
– 7x + 12 = 0.
Pour cela, on devra factoriser (si cela est
possible) le premier membre.
On constate que l’expression (x2
– 7x) peut se mettre sous la forme :
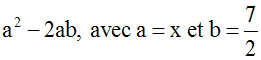
Or, (a – b)2 = a2 –
2ab + b2 implique a2
– 2ab = (a – b)2 – b2
On obtient donc :
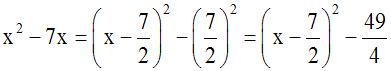
En remplaçant dans l’équation donnée, x2
– 7x par son égale :
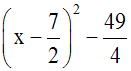
on obtient :

Pour qu’un produit de facteurs soit nul il
faut et il suffit que l’un au moins de ces
facteurs le soit ; donc :

Conclusion :
L’équation donnée admet dans R les
trois racines : –2, –1, 0, 3 et 4.
L’ensemble des solutions de cette équation
est donc :
{–2 ; –1 ; 0 ; 3 ;
4}.
Remarque
L’équation donnée dans l’énoncé est dite à
une inconnue x, du 5ème
degré par rapport à cette inconnue ;
il suffit de développer le premier membre et
de constater
que le plus
grand exposant
de l’inconnue x est 5.
Ainsi, à l’aide des identités
remarquables et de la propriété énoncée au
4-3-1, on est parvenu à la résoudre.
On dit que
nous avons ramené
la résolution d’une équation du 5ème
degré à celle d’un certain nombre
d’équations du 1er degré.
Ainsi, souvent,
la
connaissance des identités remarquables et
de la propriété énoncée au 4-3-1
nous permet de
résoudre des équations dont le degré par
rapport à l’inconnue est strictement
supérieur
à 1.
Identités remarquables - équations - systèmes
d'équations - Septième partie
4-4- Systèmes d’équations
4-4-1 Définition
On te donne deux
équations telles que chacune d’elles
contient exactement et les mêmes, deux inconnues x et y et est
du premier degré par rapport à chacune de
ces inconnues.
Tu obtiens ainsi un
système de deux
équations à deux inconnues, x et y, du
premier degré par rapport à x et à y.
La forme générale de ce
système
est :
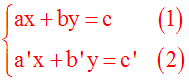
avec a, b, a’, b’ des
coefficients réels généralement
non nuls
quelconques ; c et c’ des coefficients réels
quelconques ; x et y les deux inconnues.
Résoudre ce système consiste à
trouver par le calcul les couples (x ; y)
vérifiant
simultanément
le première équation (1) et la
seconde équation (2).
Exemples :
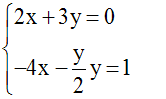
est un système de deux équations à deux
inconnues, x et y, du premier degré par
rapport à x et à y.
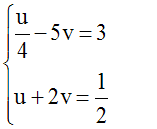
est un système de deux équations à deux
inconnues, u et v, du premier degré par
rapport à u et à v.
4-4-2 Résolution du système de deux
équations à deux inconnues, du premier degré
par rapport à ces inconnues
Résolution par comparaison
Soit à résoudre le système :
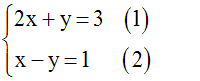
On peut déduire de l’équation (1) y en
fonction de x ; on écrit :
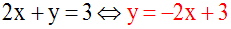
On peut déduire de l’équation (2) y en
fonction de x ; on écrit :
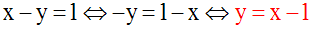
On compare les deux
valeurs obtenues de y en écrivant
qu’elles doivent
être identiques :
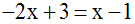
On obtient ainsi une équation en x, du
premier degré par rapport à x, qu’on sait
résoudre :
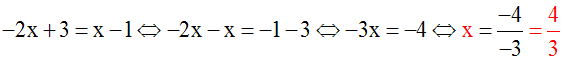
On obtient ainsi la valeur de x.
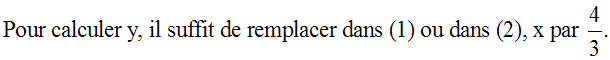
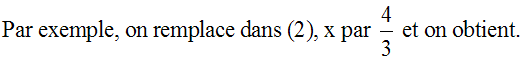
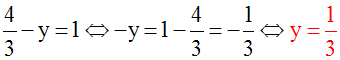
On obtient ainsi la valeur de
y.

Résolution par élimination
Soit à résoudre le
système :
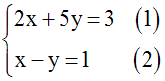
Multiplions les deux membres de (2) par
5 différent
de 0 ; on
obtient une équation logiquement
équivalente :
5x – 5y = 5
Donc le système donné est logiquement
équivalent au système suivant :
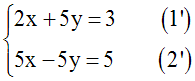
En additionnant membre à membre les deux
équations de ce système, on obtient :
(2x + 5y) + (5x – 5y) = 3 + 5 ou 7x = 8 ou
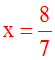
On a ainsi calculé la
valeur de l'inconnue x
par
élimination de y.
Pour calculer y, il suffit de remplacer dans
(1’) ou dans (2’), x par cette valeur
calculée.

Ainsi, le système
donné admet
une seule
solution, le couple :
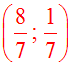
Résolution par substitution
Reprenons le système ci-dessus :
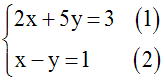
De (2), on peut
déduire x en fonction de y :
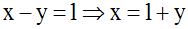
En remplaçant
dans (1), x par son égale (1 + y),
on obtient une équation en y :
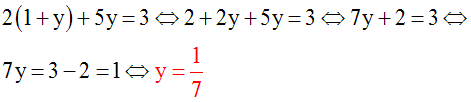
(2)
donne :
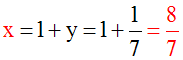
On retrouve
la même solution :
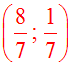
Méthode générale de résolution
Système de la
forme :
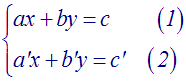
avec a, b, a’,
b’, nombres réels non nuls quelconques ; c
et c’ nombres réels quelconques
Soit à résoudre le
système :
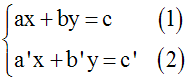
avec a, a’, b, b’, nombres réels
non nuls
quelconques ; c et c’
nombres réels quelconques
En multipliant les deux membres de (1) par
a’ différent de 0, on obtient
l’équation logiquement équivalente :
aa’x + ba’y = ca’
En multipliant les deux membres de (2) par
(–a) différent de 0, on obtient
l’équation logiquement équivalente :
(–a)a’x + (–a)b’y = (–a)c’
Le système donné est donc logiquement
équivalent à :

En additionnant membre à membre, on obtient
:
(aa’x + ba’y) + (–aa’x – ab’y) = ca’ – ac’
ou
ba’y – ab’y = ca’ – ac’ ou
(ba’ – ab’)y = ca’ – ac’ ou
(–1) (ba’ – ab’)y = (–1)( ca’ – ac’) ou
(ab’ – ba’)y =
ac’ – ca’
En multipliant les deux membres de (1) par
b’ différent de 0, on obtient
l’équation logiquement équivalente :
b’ax + b’by = b’c
En multipliant les deux membres de (2) par
(–b) différent de 0, on obtient
l’équation logiquement équivalente :
(–b)a’x + (–b)b’y = (–b)c’
Le système donné est donc logiquement
équivalent à :
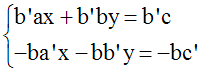
En additionnant membre à membre, on obtient
:
(b’ax + b’by) + (–ba’x – bb’y) = b’c – bc’
ou
b’ax – ba’x = b’c – bc’ ou
(b’a – a’b)x = b’c – bc’ ou
(ab’ – ba’)x =
cb’ – bc’
On obtient donc les
deux égalités permettant,
sous certaines
conditions,
de calculer les inconnues x et y :
(ab’ – ba’)y = ac’ – ca’ (3)
(ab’ – ba’)x = cb’ – bc’ (4)
Premier cas :
(ab’ – ba’) =
ac’ – ca’ = cb’ – bc’ = 0
On obtient :
0y = 0
0x = 0
Pour tout
réel x, pour
tout réel y,
ces deux
dernières équations
sont vérifiées.
Le système
admet une infinité de solutions (x ; y),
avec x et y nombres réels.
Or, (ab’ – ba’) = ac’
– ca’ = cb’ – bc’ = 0 donne :
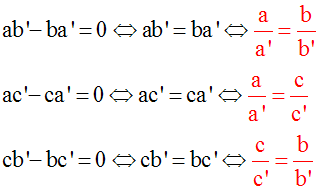
Finalement,
on obtient :
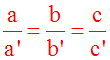
Conclusion :

Deuxième cas :
(ab’ – ba’)
= 0 et [(ac’ – ca’) différente de 0
ou (cb’ – bc’) différente de 0]
Dans ce cas on obtient
un des systèmes suivants :
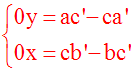
avec les quantités (ac’ – ca’) et (cb’ –
bc’) différentes de 0
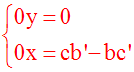
avec les quantités (cb’ – bc’) différente de
0 et (ac’ – ca’) nulle
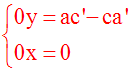
avec les quantités (ac’ – ca’) différente de
0 et
(cb’ – bc’)
nulle
Le premier système n’admet aucune solution
(x ; y) avec x et y nombres réels
car une quantité
nulle (premier membre) ne peut être
simultanément égale à une autre quantité
non nulle :
ac’ – ca’ ou cb’ – bc’
Le second
système n’admet aucune solution (x ; y) avec
x et y nombres réels
car sa seconde
équation est impossible [une quantité nulle (0 . x) ne peut être
simultanément égale à (cb’ – bc’)
différente de 0].
Le troisième
système n’admet aucune solution (x ; y) avec
x et y nombres réels
car sa première équation est impossible [une
quantité nulle (0 . y) ne peut être
simultanément égale à (ac’ – ca’)
différente de 0].
Par ailleurs, (ab’ – ba’) = 0 est
logiquement équivalente à :
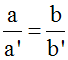
Conclusion :
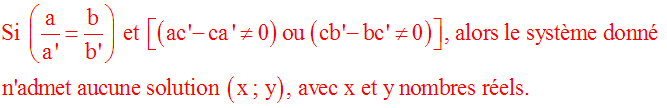
Troisième cas :
(ab’ – ba’)
non nulle
On peut alors diviser
les deux membres de chacune des équations
(3) et (4) par
la quantité
non
nulle (ab’ – ba’) ;
on obtient ainsi :
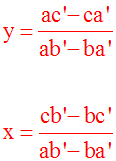
Conclusion :
Si (ab’ –
ba’) est différente de 0, alors le système
donné admet une seule solution (x ; y) :
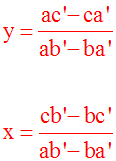
Conclusion
générale
Soit à résoudre
le système :

avec a, a’, b, b’, nombres réels non nuls
quelconques ; c et c’ nombres réels
quelconques
La quantité
(ab’ – ba’) est nommé déterminant du
système ou encore déterminant de Cramer.
On pose D = ab’ – ba’.
Si D est nul alors le système admet
une infinité de solutions ou
est impossible.
Si D est différent de 0 alors le
système admet une seule solution.
Méthode rapide pour calculer les solutions
du système, si elles existent,
c'est-à-dire si :
D = ab’ – ba’
est non nulle
On reprend le système :

Calcul du
déterminant de Cramer, D
Définition préalable
m, n, p et q étant quatre nombres réels
quelconques, chacune des quantités :
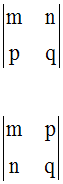
sont appelées déterminants.
Elles se calculent comme suit :
1-
On effectue d'abord les produits en croix,
c’est-à-dire :
m.q
d’abord
et n.p
ensuite.
2-
On soustrait le
second
produit (n.p) du premier (m.q) ; on
obtient ainsi :
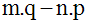
On écrit :
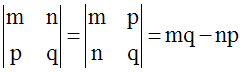
Retour à notre cas
Pour notre système ci-dessus, le
déterminant de Cramer, D, est donc la
quantité supposée non nulle :
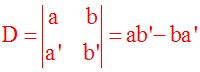
Calcul de x et
de y
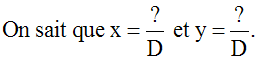
Exemples :
Soit à
résoudre :
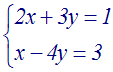
Solution
On a :
a = +2 ; b = +3 ; c =
+1 ; a’ = +1 ; b’ = – 4 ; c’ = +3
On calcule d’abord le déterminant D de ce
système.
D
= ab’ – ba’ = (2).( – 4) – (+3).(+1) = (– 8)
– (+3) = –
11, différent de 0.
Donc le système admet une seule solution
(x ; y) telle que :
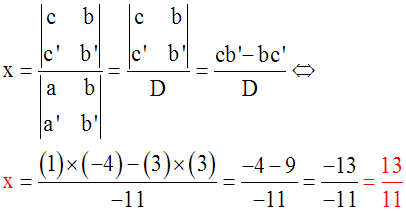
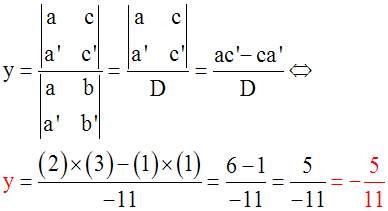
Soit à résoudre le système :
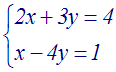
Solution
On a :
a = +2 ; b = +3 ; c =
+4 ; a’ = +1 ; b’ = –4 ; c’ = +1
On calcule d’abord le déterminant D de ce
système.
D
= ab’ – ba’ = (+2).( – 4) – (+3).(+1) = (–
8) – (+3) =
– 11, différent de 0.
Donc le système admet
une seule solution (x ; y) telle que :
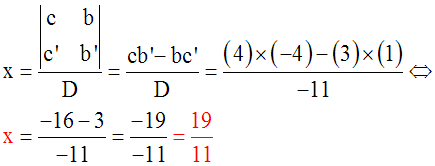
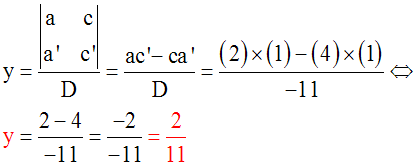
Soit à résoudre
le système :
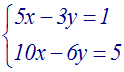
Solution
On a :
a = +5 ; b = –3 ; c =
+1 ; a’ = +10 ; b’ = –6 ; c’ = +5
On calcule d’abord le déterminant D de ce
système.
D
= ab’ – ba’ = (+5).( – 6) – (–3).(+10) = (–
30) – (– 30) =
– 30 + 30
= 0.
Donc on a un des deux cas suivants :
- le système admet une infinité de solution
- le système est impossible
On doit calculer les deux quantités : (ac’ –
ca’) et (cb’ – bc’)
On a :
ac’ – ca’
= (+5)(+5) – (+1)(+10) = +25 – (+10) = +15
différent de
0.
[D = 0 et
(ac’ – ca’) différent de 0] ; alors le
système est impossible.
Soit à résoudre
le système :
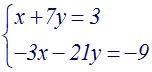
Solution
On a :
a = +1 ; b = +7 ; c = +3 ; a’ = – 3 ; b’ =
–21 ; c’ = – 9
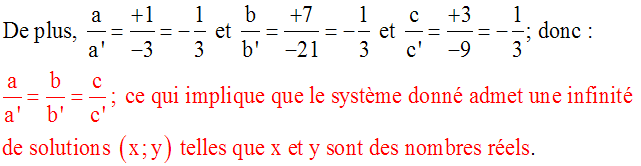
Trouvons quelques unes de ces solutions.
Fixons x ; prenons par exemple x = + 4.
La première équation donne :
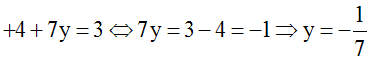

Fixons y ; prenons par exemple y = + 1.
La seconde équation donne :
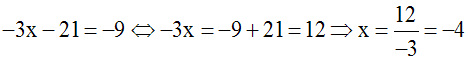
Nous remarquons que (– 4 ; + 1) est
également une solution de la première
équation.
Donc (– 4 ;
+ 1)
est une seconde
solution du système donné.
Résoudre le
système :
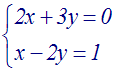
Solution
a = +2 , b = +3 , c = 0 , a’ = +1 , b’ = –2
, c’ = +1
D
= ab’ – ba’ = (+2)( –2) – (+3)(+1) = (–4) –
(+3) = –7
différent de
0.
Donc
le système admet
une seule solution (x ; y) telle que :
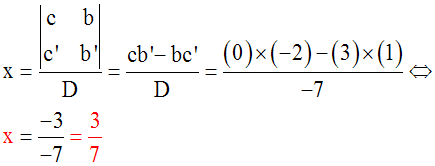

Résoudre le
système :
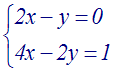
Solution
a = +2 , b = –1 , c = 0 , a’ = +4 , b’ = –2
, c’ = +1
D
= ab’ – ba’ = (+2)( –2) – (–1)(+4) = (–4) –
(–4) = – 4 + 4
= 0.
Par ailleurs, on a :
ac’ – ca’
= (+2)(+1) – (0)(+4) =
+2 – 0 = +2
différent de 0.
Donc
le système donné
n’admet aucune solution (x ; y) telle que x
et y sont des nombres réels.
Résoudre
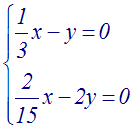
Solution
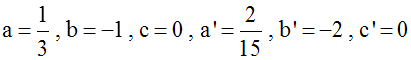
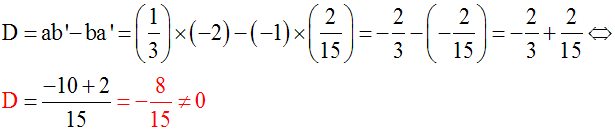
Donc
le système admet
une seule solution.
On a :
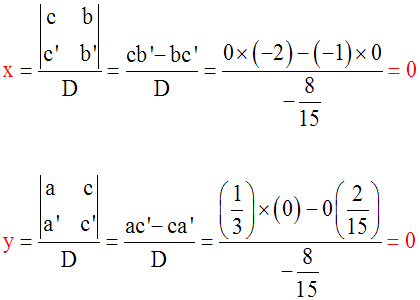
4-4-3 Systèmes particuliers se ramenant à
la résolution d’un système de deux équations
à deux inconnues, du premier degré par
rapport à ces inconnues
Système de la
forme :

Solution
xy = b implique 2xy = 2b
x + y = a implique (x + y)2 = a2
ou x2 + 2xy + y2 = a2
En remplaçant dans cette dernière égalité
2xy par 2b, on obtient :
x2 + 2b + y2 = a2
ou x2 + y2 = a2
– 2b
Premier cas :
(a2 –
2b) largement positive
On obtient donc le système :

En soustrayant membre
à membre, on obtient :
x2 + y2 – 2xy = a2
– 2b – 2b ou (x – y)2 = a2
– 4b
Si (a2
– 4b) est largement positive,
alors on peut écrire :
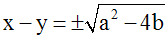
Ainsi, le système donné est logiquement
équivalent à l’ensemble des deux systèmes
suivants :
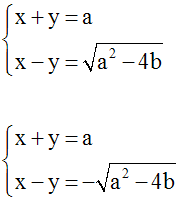
En résolvant ces systèmes, on obtient
finalement les solutions du système donné.
Si
(a2 – 4b) est strictement
négative,
alors le système
n’admet aucune
solution (x ; y) telle que x et y nombres
réels.
Deuxième cas :
(a2 –
2b) strictement négatif
x2 + y2
étant une quantité positive
ne peut être égale à
(a2 – 2b) négative.
Le système
n’admet aucune solution (x ; y) telle que x
et y nombres réels.
Exemples
Résoudre
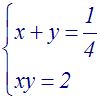
Solution
On calcule d’abord (a2 – 2b) :
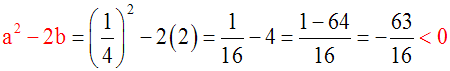
Le système
n’admet aucune
solution (x ; y) telle que x et y nombres
réels.
Résoudre
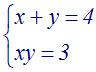
Solution
On calcule d’abord (a2 – 2b) :
a2
– 2b = (4)2
– 2(3) = 16 – 6 = 10
> 0
x + y = 4 implique (x + y)2 = 16
ou x2 + 2xy + y2 = 16
En remplaçant dans cette dernière égalité
2xy par 2.(3) = 6, on obtient :
x2 + 6 + y2 = 16 ou x2
+ y2 = 16 – 6 = 10
On obtient donc le système :
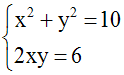
En soustrayant membre à membre, on obtient :
x2 + y2 – 2xy = 10 – 6
= 4 ou (x – y)2 = 4
> 0
On obtient ainsi :
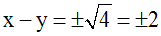
Ainsi, le système donné est logiquement
équivalent à l’ensemble des deux systèmes
suivants :
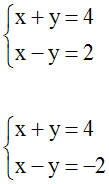
Le premier
système, par addition membre à membre, donne :
2x = 6 ou x = 3
En remplaçant x par 3 dans une de ses
équations on trouve y = 1.
Le système
donné admet donc comme première solution,
(3 ; 1).
Le deuxième
système, par addition membre à membre, donne :
2x = 2 ou x = 1
En remplaçant x par 1 dans une de ses
équations on trouve y = 3.
Le système
donné admet donc comme deuxième solution
(1 ; 3).
Conclusion
L’ensemble des solutions du système donné
est :
{(3 ; 1) ,
(1 ; 3)}.
Remarque importante :
(3 ; 1) et (1 ; 3)
sont deux couples
différents,
car, (a ; b)
est égal à
(b ; a) si seulement si
a = b.
En soustrayant membre
à membre, on obtient :
x2 + y2 – 2xy = 1 – 2
= –1 <
0
Or,
x2 +
y2 – 2xy = (x – y) 2
étant positive
ne peut être égale
à (–1), quantité
négative.
Le système n’admet aucune solution (x ;
y) telle que x et y nombres réels.