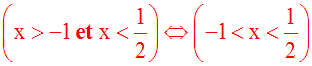
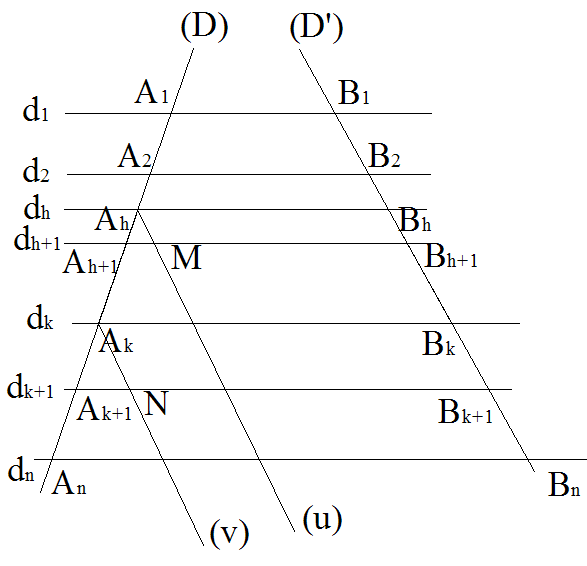
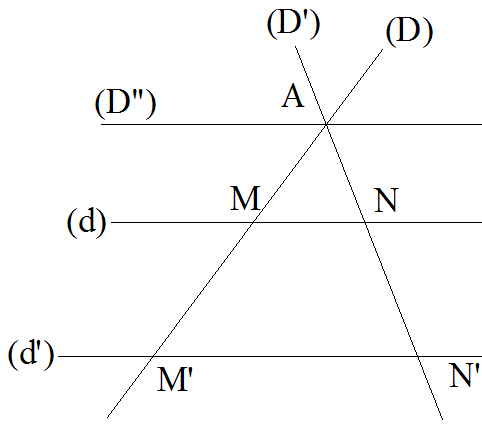
Équation d'une droite et position relative de deux droites -3ème
Je retiens
Dans un repère orthonormal (x'x , y'y), d'origine O, la forme générale de l'équation d'une droite d non parallèle à x'x et à y'y est :
y = a x + b avec a différent de zéro, étant nommé coefficient directeur de d ou encore pente de d.
Pour x nul, l'ordonnée y vaut b. d passe donc par le point A (0 ; b). b est donc l'ordonnée du point d'intersection A de d avec l'axe des ordonnées. On l'appelle également ordonnée à l'origine.
Soient dans ce même repère, deux droites d et d' (d et d' non parallèles à x'x et à y'y), d'équations respectives :
y = a x + b et y = a' x + b', avec a et a' différents de 0 et b différent de b'.
d et d' sont dites perpendiculaires si et seulement si le produit de leurs coefficients directeurs a et a' est égal à - 1, c'est-à-dire a . a' = - 1
d
et d' sont dites parallèles
si et seulement si leurs coefficients directeurs a
et a' sont égaux, c'est-à-dire
a = a'
Cas particuliers
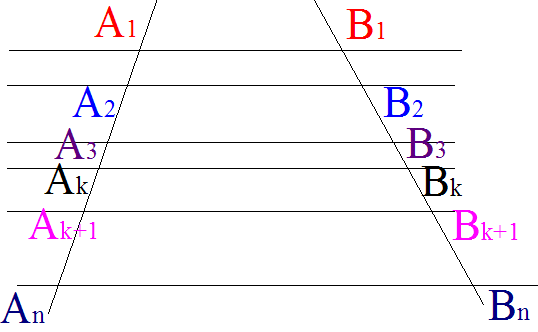
Soit un repère orthonormal (x'x , y'y), d'origine O.
L'ensemble des points M du plan de ce repère ayant leurs abscisses nulles est l'axe y'y des ordonnées.
L'ensemble des points N du plan de ce repère ayant leurs ordonnées nulles est l'axe x'x des abscisses.
Toute droite D parallèle à l'axe x'x des abscisses a pour équation de la forme y = a avec a constant.
Toute droite D' parallèle à l'axe y'y des ordonnées a pour équation de la forme x = b avec b constant.
Je m'entraîne
Soit
un repère orthonormal (x'x , y'y), d'origine O.
Trouve l'équation de la droite d passant par les points A (-5 ; 2) et
B (4
; -1).
Trouve l'équation de la droite d' passant par A et perpendiculaire à d.
On te donne le point M (0 ; 1) et la droite d" pivotant autour de M et ayant
pour équation y = mx + n, m étant un nombre quelconque différent de 0 et n étant
un nombre quelconque.
Pour
quelle valeur de m la droite d'' est :
parallèle à d ? perpendiculaire à d ?
Solution
La forme générale de l'équation de la droite d est y = ax + b.
A appartenant à d, ses coordonnées doivent donc vérifier l'équation de d et on peut écrire :

B appartenant à d, ses coordonnées doivent donc vérifier l'équation de d et on peut écrire :
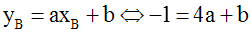
On obtient ainsi le système d'équations à deux inconnues a et b :
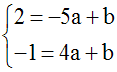
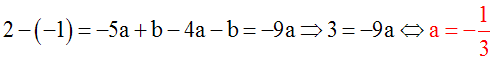

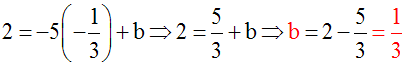
L'équation de d est donc :
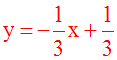
La forme générale de l'équation de la droite d' est y = kx + h.
A appartenant à d', ses coordonnées doivent donc vérifier l'équation de d' et on peut écrire :
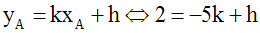
d' étant perpendiculaire à d, le produit de son coefficient directeur k par celui de d doit être égal à -1; donc :
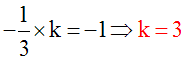
En remplaçant k par 3 dans la relation 2 = -5k + h, on trouve h :

L'équation de d' est donc :
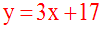
L'équation de la droite d'' est y = mx + n.
M devant appartenir à d'', ses coordonnées doivent donc vérifier l'équation de cette dernière et on peut écrire :
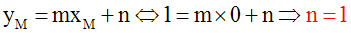
L'équation de d'' s'écrit alors :
y = mx + 1
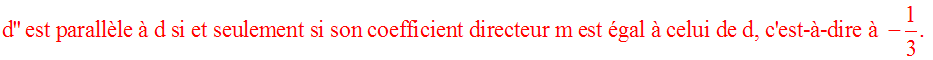

Soit
un repère orthonormal (x'x , y'y), d'origine O.
On te donne deux droites d et d' d'équations respectives :
y = 2x + 5 et y = - x - 3
Dis
pourquoi d et d' sont concourantes. Calcule alors les coordonnées de leur point
d'intersection A.
Solution
d et d' ont des coefficients directeurs 2 et -1 différents; donc elles ne sont pas parallèles. Elles sont donc concourantes.
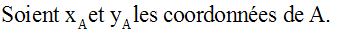
A appartenant à d, ses coordonnées doivent donc vérifier l'équation de d et on peut écrire :
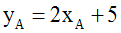
A appartenant à d', ses coordonnées doivent donc vérifier l'équation de d' et on peut écrire :
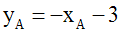
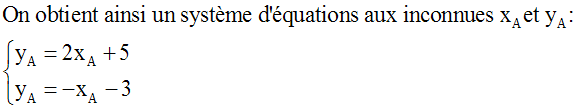
Sa résolution donnera les coordonnées de A.
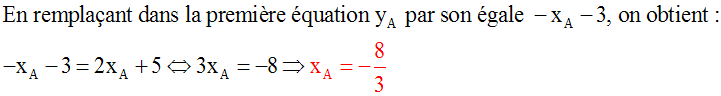
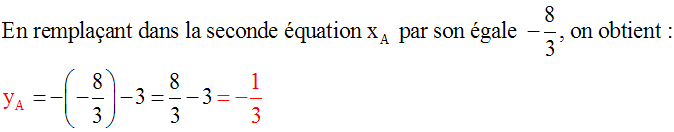
Soit
un repère orthonormal (x'x , y'y), d'origine O.
On te donne la droite d d'équation y = x - 5.
Dis pourquoi le point A (- 1 ; 1) n'appartient pas à d. Trouve l'équation de la
droite d' passant par A et perpendiculaire à d.
Trouve l'équation de la droite d'' passant par A et parallèle à d.
Solution
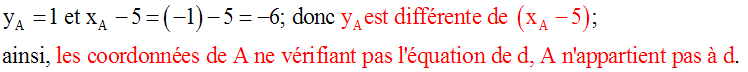
La forme générale de l'équation de la droite d' est y = ax + b.
A appartenant à d', ses coordonnées doivent donc vérifier l'équation de d' et on peut écrire :
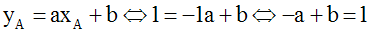
d' devant être perpendiculaire à d, le produit de son coefficient directeur, a, par celui de d qui est 1, doit être égal à -1; donc : a . (1) = -1 ou a = -1.
En remplaçant dans -a + b = 1, a par sa valeur -1 on calcule b :
-(-1) + b = 1 ou 1 + b = 1 ou b = 0
L'équation de d' est donc y = -x + 0 ou y = -x.
d' est donc la seconde bissectrice du repère.
La forme générale de l'équation de la droite d'' est y = wx + u.
A appartenant à d'', ses coordonnées doivent donc vérifier l'équation de d'' et on peut écrire :
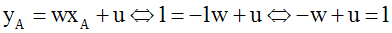
d'' devant être parallèle à d, son coefficient directeur, w, doit être égal à
celui de d, c'est-à-dire 1;
donc w = 1.
En remplaçant dans -w + u = 1, w par son égale 1, on trouve u :
-1 + u = 1 ou u = 1 + 1 = 2
L'équation de d'' est donc
y = 1 . x + 2 ou y = x + 2.
distance et Pythagore dans un repère orthonormal
Je retiens
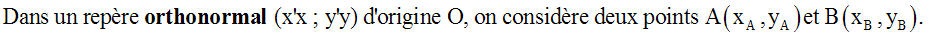
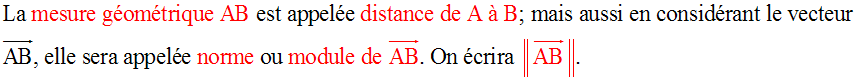
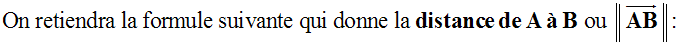
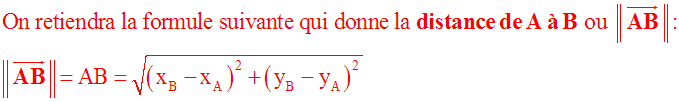
Je m'entraîne
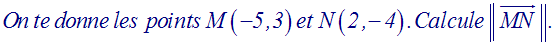
On te donne les
trois points C (0 ; 15), D (4 ; 0) et E (14 ; 11).
Le triangle (CDE) est-il équilatéral ?
Solution
On a :

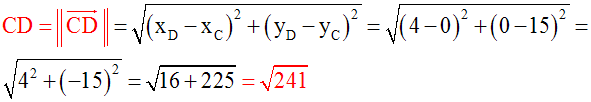
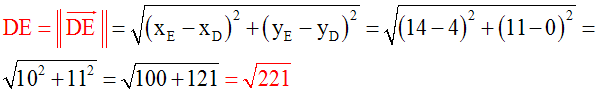
Donc DE n'est pas égale à CD; le triangle (CDE) n'est donc pas équilatéral.

Le triangle (IJK) est-il un triangle rectangle ?
(ici on appliquera la formule donnée ci-dessus pour conclure si ce triangle
vérifie ou non la réciproque du théorème de Pythagore)
Solution
On a :
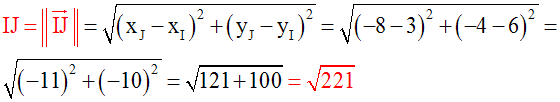
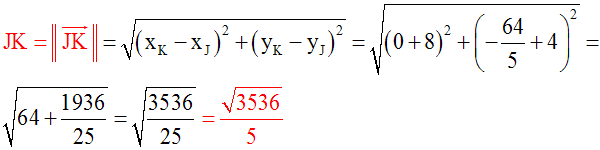
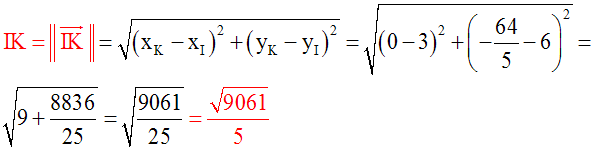
Ainsi, on a :

On sait que si le carré de la longueur d'un côté d'un triangle est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est un triangle rectangle. C'est la réciproque du théorème de Pythagore.
Donc, le triangle (IJK) dont les longueurs vérifient la relation :
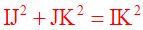
est un triangle rectangle.
Son angle droit est celui qui est opposé à son hypoténuse [IK]; donc son angle droit est en J.
Pythagore 3ème
On prend comme unité de mesure des longueurs le centimètre.
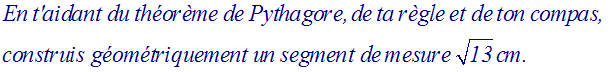
Solution
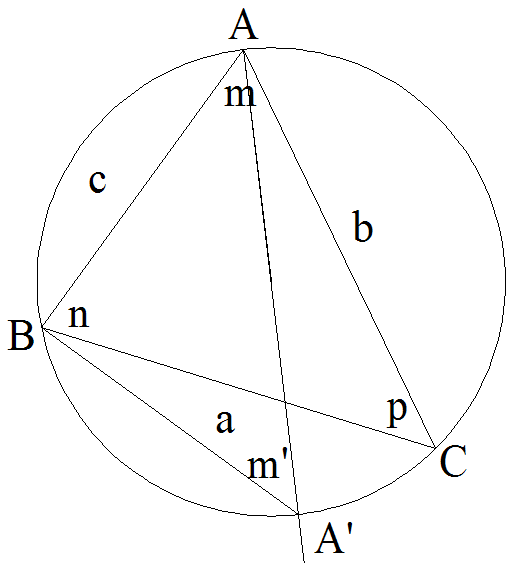
Soit un triangle rectangle (ABC), rectangle en A.
Soient a, b et c les longueurs respectives de son hypoténuse [BC] et de ses deux autres côtés.
Le théorème de Pythagore donne :
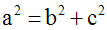
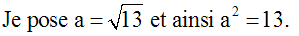
Il me faut donc trouver deux nombres entiers b et c tels que la somme de leurs carrés soit 13.
b = 2 et c = 3 satisfont cette condition.
Il suffit donc de construire, avec ma règle et mon compas, un triangle rectangle dont les côtés de l'angle droit aient pour longueurs 2 cm et 3 cm.
Construction
Je trace d'abord une droite (xy) sur laquelle je place un point A.
Du point A, avec une ouverture de compas quelconque, je trace de part et d'autre de A deux arcs de cercles qui coupent (xy) aux points M et N.
Donc par construction A est milieu de [MN].
Je dois maintenant construire la médiatrice de [MN], qui passant par A, sera une droite perpendiculaire à (xy).
Du point
M, avec une ouverture de compas
supérieure à la moitié de la longueur
MN, je trace, de part et d'autre de (xy),
deux arcs de cercle (m) et (n).
Du point N, avec la même ouverture de
compas, je trace, de part et d'autre de
(xy), deux autres arcs de cercle (m') et
(n').
Ces quatre
arcs de cercle se coupent deux à deux en
deux points P et Q.
(PQ) sera donc la médiatrice de [MN].
J'ai donc finalement construis un angle droit qui est :
{[Ax) , [AP)}
Avec ma règle et une ouverture de compas égale à 2 cm et à partir de A, je place le point B sur [AP).
Avec ma règle, une ouverture de compas égale à 3 cm et à partir de A, je place le point C sur [Ax).
J'obtiens finalement le triangle rectangle (ABC), rectangle en A et recherché; en effet :
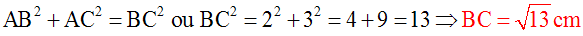
Coordonnées d'un vecteur et translation
Je retiens

Je m'entraîne
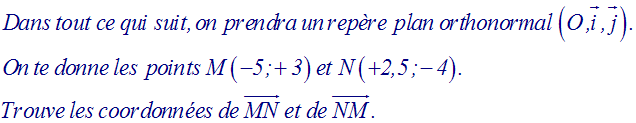
Solution
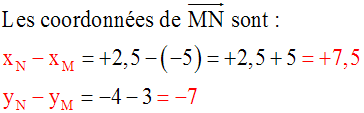
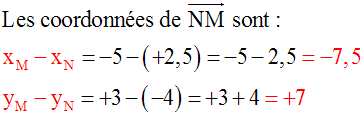
Conclusion

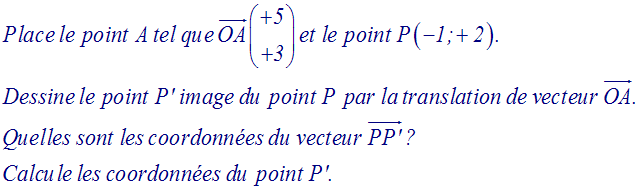
Solution

On place ensuite le point P d'abscisse -1 et d'ordonnée +2.

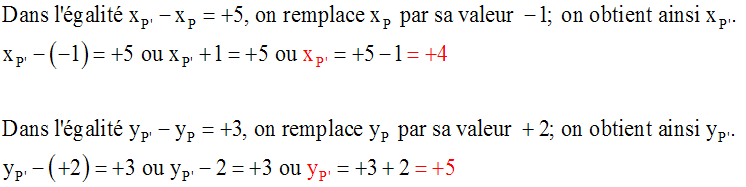
Place le point Q (2 ; -3).
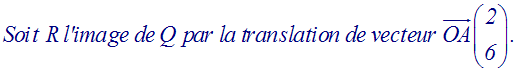
Construis R et calcule ses coordonnées.
Solution
Placement de Q
Il suffit de mener la droite x = 2 parallèle à l'axe des ordonnées et la droite y = -3 parallèle à l'axe des abscisses. L'intersection de ces deux droites sera le point Q.
Construction de R

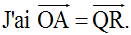
Or, je sais que deux vecteurs équipollents ou égaux ont leurs composantes scalaires, de même nom, égales; donc :
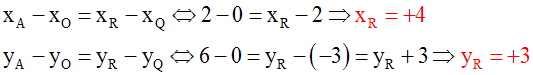
Une translation t transforme le point I (8 ; -1) en J (3 ; 2) . Calcule les coordonnées du vecteur qui définit t.
Solution

Parmi les énoncés suivants, lesquels sont vrais; lesquels sont faux ?
La translation conserve les distances
La translation conserve les mesures d'angle
Il existe un point dont l'image par une translation quelconque lui soit égale
La translation conserve les mesures de surface
Solution
Tous les énoncés, à l'exclusion du troisième qui est faux, sont vrais.
identité remarquable
A titre d'exemple, résoudre les équations :

Solution
Résolution de l'équation :
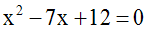
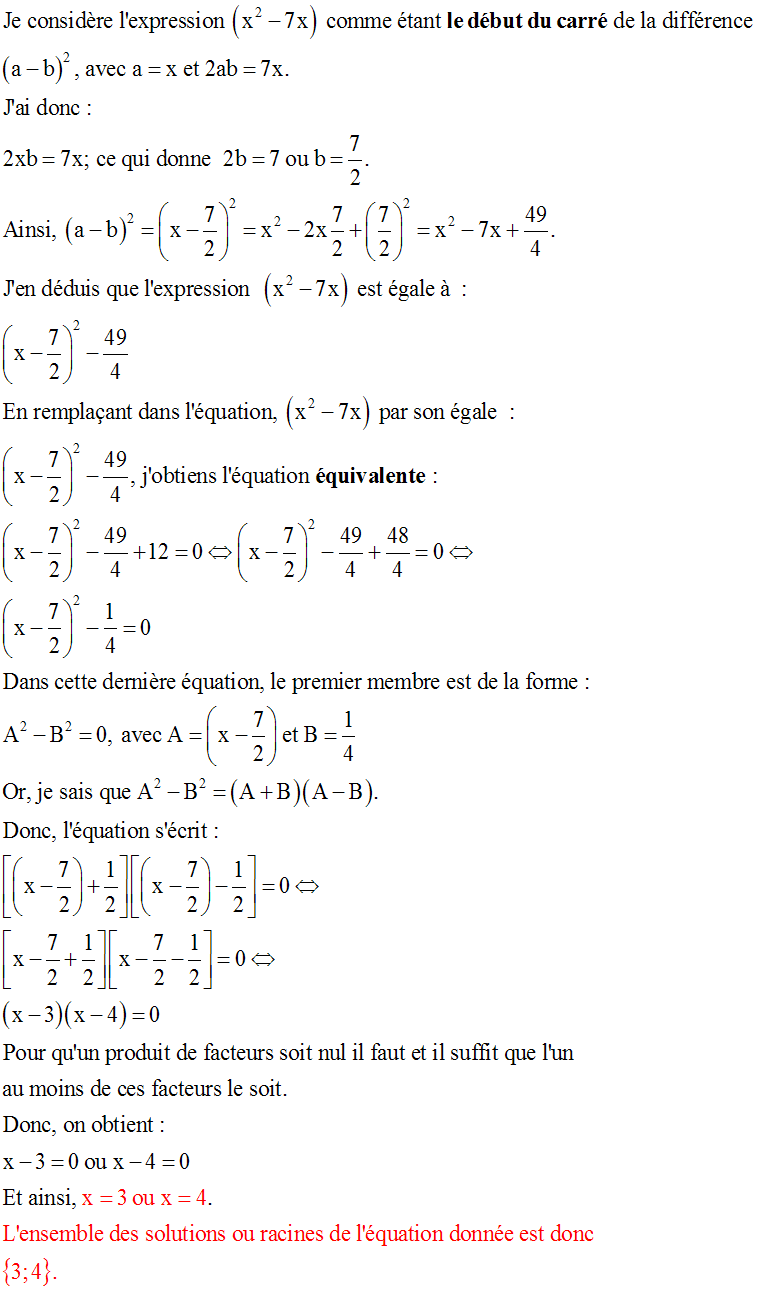
Résolution de l'équation :

D'abord, l'inconnue étant X = cosa, je dois noter la condition que doit respecter X.
En effet, je sais que le cosinus d'une mesure d'angle doit être largement compris entre -1 et +1.
Donc X doit être largement comprise entre -1 et +1; j'écris :
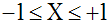
Ayant posé X = cosa, l'équation s'écrit :
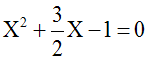
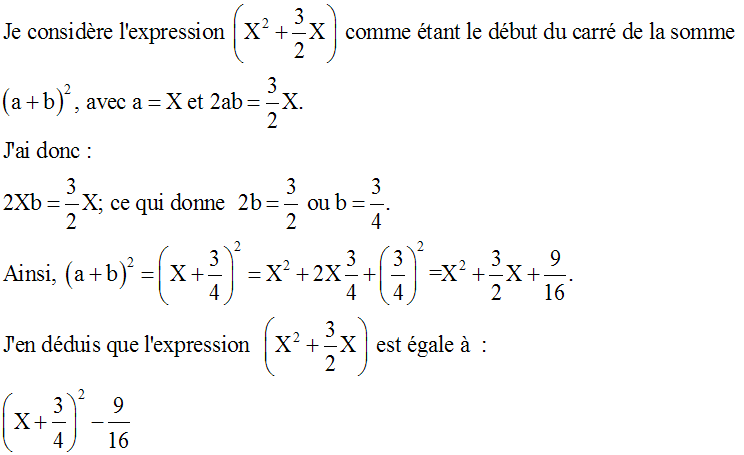


lieu géométrique d'un point mobile
S se déplace dans le plan tel que la mesure de l'angle au sommet S soit constamment égale à 120°.
Les deux bissectrices des angles intérieurs en B et en C se coupent au point W.
Quelle trajectoire décrit W lorsque S se déplace ?
Solution
Je calcule d'abord la mesure w de l'angle intérieur au sommet W, dans le triangle (WBC).
Si m et n sont respectivement les mesures des angles intérieurs en B et C dans le triangle (WBC), et sachant que la somme des mesures des angles intérieurs d'un triangle est égale à 180°, alors :
w + m + n = 180°
Or, [BW) est la bissectrice de l'angle intérieur en B, dans le triangle (SBC); donc, si b est la mesure de cet angle intérieur, alors :
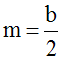
De même, [CW) est la bissectrice de l'angle intérieur en C, dans le triangle (SBC); donc, si c est la mesure de cet angle intérieur, alors :

J'ai donc :
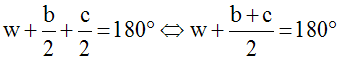
Or, dans le triangle (SBC), j'ai :
s + b + c = 180°, avec s = 120° étant la mesure de l'angle intérieur au sommet S.
Donc, b + c = 180° - s = 180° - 120° = 60°.
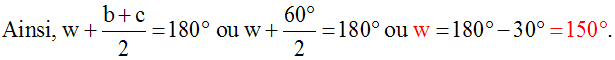
Le point W se déplace dans le plan du triangle (SBC) tel que l'angle intérieur au sommet W, dans le triangle (WBC), a une mesure constante égale à 150°; de plus les points B et C sont fixes.
Par conséquent, la trajectoire de W est un arc de cercle construit sur la corde fixe [BC], cette corde étant vue sous tout angle inscrit dans cet arc de cercle, de mesure constante égale à 150°.
Cette trajectoire sera appelée arc capable.
Construction de l'arc capable
Cet arc passant par W, B et C, est donc inclus dans le cercle circonscrit au triangle (WBC).
Par ailleurs, je sais que la tangente à ce cercle menée par C forme avec [CB) un angle dont la mesure est égale à 150°.
Ainsi, pour construire la trajectoire, je procède comme suit :
- Je construis la médiatrice (d) de [BC]
- Du point C, je mène la demi-droite [Cx) incluse dans le demi plan défini par la droite (BC) et ne contenant pas W, l'angle {[CB) , [Cx)} ayant pour mesure 150°
- L'intersection O de [Cx) et de (d) sera donc le centre du cercle circonscrit au triangle (WBC)
- Avec une ouvertrure de mon compas égale à OC, je trace ce cercle
- La trajectoire décrite par W sera donc l'arc capable (BWC).une animation illustrant ce qu'est un arc capable
tu as dit translation ?
L'image de (F) par la
symétrie centrale de centre O
est (F'); celle de (F') par la
symétrie centrale de centre O'
(O et O' distincts) est (F").
Quelle est la transformation qui
qui nous fait passer directement
de (F) à (F") ?
Solution
Je nomme S la symétrie centrale de centre O et S' celle de centre O', O et O' étant distincts.
Si M est un point quelconque de (F), alors son image par S est le point M' tel que O est milieu de [MM'].
De plus, lorsque M décrit (F), M' décrit (F') image de (F) par la symétrie S.
L'image de M' par S' est le point M'' tel que O' est milieu de [M'M''].
De plus, lorsque M' décrit (F'), M'' décrit (F'') image de (F') par la symétrie S'.
Dans le triangle (MM'M''), on a :
O milieu de [MM'] et O' milieu de [M'M''].
Or, je sais que le segment joignant les milieux de deux côtés d'un triangle a son support parallèle au troisième côté et sa longueur égale à la moitié de celle de ce côté.

trouve l'erreur
Un élève a rédigé la démonstration suivante :
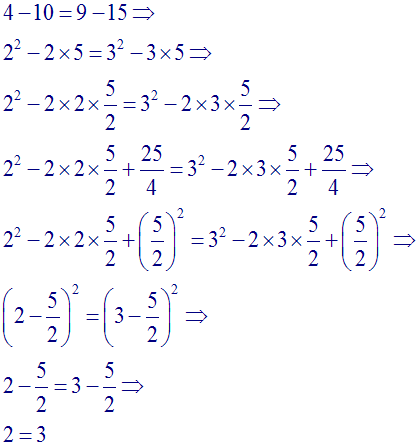
Trouve l'erreur commise.
Solution
L'erreur a été commise lors du passage de la sixième à la septième ligne.
En effet, l'égalité :
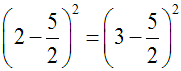
est logiquement équivalente à :
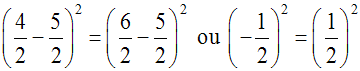
Cependant, cette dernière égalité ne peut pas impliquer :
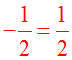
Simplifions par A...
La
quantité sous le radical d'une
racine carrée doit être toujours
largement positive.
On a l'inéquation :
Multiplions les deux membres par
la quantité non nulle x, on
obtient :
Ce raisonnement
manque de rigueur
et ce procédé de
calcul est faux.
ce qu'il ne faut
jamais écrire ou faire au brevet
Simplifier une
expression par une quantité A
sans se soucier
de la condition portant sur A, à
savoir :
A doit être différente
de 0, est considéré
comme un manque de
rigueur.
Chaque fois que
l'on a à simplifier par une
quantité A,
ne pas oublier d'expliciter
préalablement la
condition : A différente de 0.
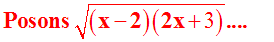
Manipuler
des racines carrées sans avoir
indiqué au préalable
les valeurs de la variable x
pour lesquelles la quantité sous
le radical est largement
positive
est un
manque de rigueur et est
considéré comme une erreur.
Dans notre
exemple, on devait indiquer
préalablement aux
calculs que (x - 2)(2x
+ 3) doit être largement
positif, c'est-à-dire :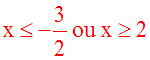
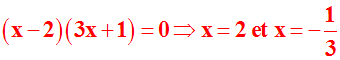
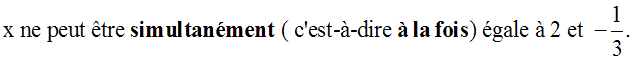
Il faudra
remplacer
la conjonction "
et
" par la
disjonction "
ou
".
On devait
donc écrire :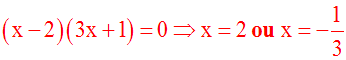
a : mesure
d'un angle aigu,
en radian
cos
(a) = k, avec k nombre
strictement inférieur à 0 ou
strictement supérieur à + 1
Le résultat de ce calcul est
faux. En effet
la valeur du cosinus d'un angle
aigu
quelconque est toujours
largement compris entre 0 et + 1.
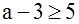
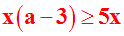
En effet, on a multiplié les
deux membres de l'inéquation par
la quantité x sans se
soucier du signe de x.
Si x est
strictement négatif,
alors
le sens de l'inéquation change.
Ainsi, on devait écrire :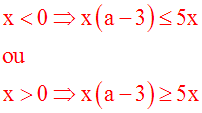
Je
construis le triangle (ABC)
sachant que les mesures
géométriques de ses côtés sont :
AB = a, BC = b et AC = c a
> b > c
Manque de rigueur dans cet
énoncé; effectivement, on devait
d'abord poser
la condition d'existence
de ce triangle avant de
procéder à sa construction, à
savoir
l'inégalité triangulaire
:
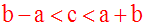
Je travaille dans
l'ensemble N
des nombres entiers naturels.
Je dois résoudre l'équation 2 x
- 1 = 0.
J'ajoute aux deux membres
l'opposé de - 1 qui est + 1;
j'obtiens :
2x - 1 + 1 = 0 + 1 ou 2x = +
1
Je divise les deux membres de
cette dernière équation par 2;
j'obtiens :
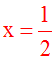
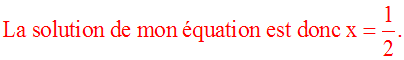

Conclusion :
Chaque fois que tu dois résoudre
une équation, relis l'énoncé
de ton
problème pour vérifier que l'on
n'a pas précisé
l'ensemble dans lequel tu
dois travailler.
Si
aucune condition n'a
été précisée, alors la
résolution de l'équation se fait
d'une manière générale.
Souvent aussi l'énoncé porte sur
des inconnues à calculer et qui
doivent
vérifier
des conditions particulières.
Par exemple, si l'inconnue à
calculer est un nombre de
personnes,
alors on devine qu'un résultat
décimal
tel que 3,45 ou négatif tel que - 5 n'a aucun sens.
Je manipule des fractions en x telles que :
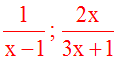
sans avoir indiqué préalablement
les conditions que doivent
vérifier les dénominateurs.
Ces
manipulations sans avoir indiqué
les conditions que doivent
vérifier les dénominateurs
est
une erreur.
On sait que
le
dénominateur d'une fraction doit
être toujours différent de 0.
Ainsi, la première expression n'a de sens que si
(x - 1) est différent de 0; ce
qui donne x différent de
1.
La seconde n'a de sens que si
(3x + 1) est différent de 0;
ce qui donne 3x différent de - 1
ou x différent de
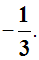
Ainsi,
avant tout calcul
sur ces expressions, on devait
poser la condition ou les
conditions que doit satisfaire
la variable.
Mon nom est Anna.
On me demande de résoudre, par
l'équation, un problème.
Il s'agit de trouver le nombre
d'enfants qui
composent une famille donnée.
J'ai posé mon équation et je
l'ai résolue; j'ai trouvé deux
valeurs X =
- 5
et X = 3 que j'ai soigneusement
encadrées.
Ma
réponse s'est arrêtée là, aucun
commentaire de plus.
Un bon exemple de raisonnement
à ne pas reproduire
dans une épreuve de brevet.
Certes, Anna a réussi à résoudre
son équation.
Mais il faut savoir qu'une
équation mathématique est
souvent
neutre
au regard des
conditions
réelles posées
au départ dans l'énoncé.
Ici, la condition portée sur
l'inconnue X de notre équation
est que la solution doit être un
nombre
entier
naturel, car il
s'agit d'enfants.
Anna devait donc, à la fin,
exclure la valeur - 5 en
justifiant.
Conclusion :
méthode à suivre pour résoudre
un problème, par l'équation.
1- lire l'énoncé
2- le relire, mais cette fois-ci
en soulignant tous les
passages pertinents, à savoir :
ceux permettant d'identifier
l'inconnue et ceux
indiquant les
conditions
que doit vérifier l'inconnue
3-
Traduire en
équation l'énoncé du problème
4-
Résoudre l'équation; à
cette étape on ne se soucie pas
des conditions;
toute
notre attention doit être portée
sur la résolution de l'équation
5- les solutions ( racines) de
l'équation, trouvées, on doit
vérifier si elles
satisfont les
conditions
identifiées à l'étape 2.
Celles ne satisfaisant pas ces
conditions seront exclues
Mon nom est
Rémi.
J'ai réussi à résoudre, par
l'équation, le problème suivant
:
Georges, un père de famille a 35
ans. Martine, sa fille aînée a
...
Dans combien
d'années
l'âge de ce père
de famille sera-t-il le
double de celui de sa
fille ?
J'ai trouvé la racine de mon
équation : - 4.
Ce
nombre étant négatif, je l'ai
exclu et j'ai déclaré que mon
problème était impossible.
Rémi croit
avoir réussi; malheureusement ce
n'est pas le cas, car il n'a pas
su
interpréter
la solution
négative.
Le temps pouvant s'exprimer
dans le passé,
comme dans le présent ou le
futur, la racine x = - 4
indique que l'âge
du père était le double de celui
de sa fille, il y à 4 ans de
cela.
La vérification est facile : il
suffit de retrancher 4 à chacun
des deux âges et de constater
que la condition a
été déjà satisfaite
(dans le passé).
Clémentine écrit :
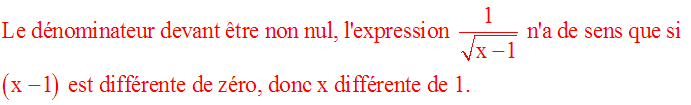
Certes, le dénominateur doit être différent de 0.
Mais aussi la quantité se trouvant sous le radical doit être largement positive, car la racine carrée d'une quantité négative n'existe pas dans l'ensemble des nombres que l'on a appris.
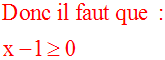
Ce qui donne :
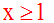
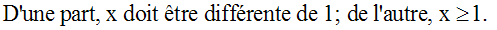
Donc finalement l'expression donnée n'a de sens que si x > 1.
Un élève, lors d'un calcul, trouve le résultat suivant :
1 + sina > 3
Cette inégalité est fausse.
En effet, on sait que le sinus d'un angle aigu est toujours largement compris entre 0 et 1.
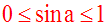
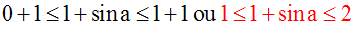
Conclusion :
Gardons toujours à l'esprit que quel que soit l'angle aigu, son sinus et son cosinus sont largement comprises entre 0 et 1, et quelle que soit la quantité K qu'on leur ajoute, le résultat est largement compris ente K et K + 1
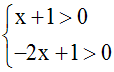
un élève écrit :

L'erreur commise, ici, est l'utilisation de la disjonction " ou "; en effet, la résolution d'une inéquation de ce type, consiste à trouver l'ensemble des solutions qui satisfont simultanément ( c'est-à-dire à la fois ) les deux inéquations.