1- Je comprends
Premier cas de figureDans le plan de ma feuille, je trace deux droites concourantes (d) et (d') au point A.
Je trace ensuite deux droites parallèles (D) et (D').
(D) rencontre (d) et (d') en E et F.
(D') rencontre (d) et (d') en G et H.
Avec ma règle graduée, je mesure les longueurs : AE, AG, AF, AH, EF, GH, FH, EG.
Je constate que :
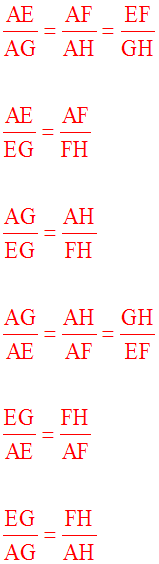
Deuxième cas de figure
Dans le plan de ma feuille, je trace deux droites concourantes quelconques (d) et (d').
Je trace ensuite trois droites parallèles (D), (D') et (D") telles que :
(D) rencontre (d) et (d') en E et F
(D') rencontre (d) et (d') en G et H
(D") rencontre (d) et (d') en I et J
Avec ma règle graduée, je mesure les longueurs : EG, GI, EI, FH, HJ, FJ.
Je constate que :

Troisième cas de figure
Je trace un triangle quelconque (ABC).
Je place ensuite le milieu M du côté [AB] et le milieu N du côté [AC].
Je constate alors que
la droite (MN) est parallèle au troisième côté [BC].Avec ma règle graduée, je mesure les longueurs MN et BC.
Je constate que :
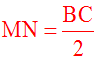
2- Je retiens et je me souviendrai
Points et segments homologues dans une projection selon une direction donnée
Soit une famille de trois droites parallèles (D), (D') et (D") rencontrant deux droites non parallèles ou sécantes (d) et (d').
La direction commune des droites parallèles est (D).
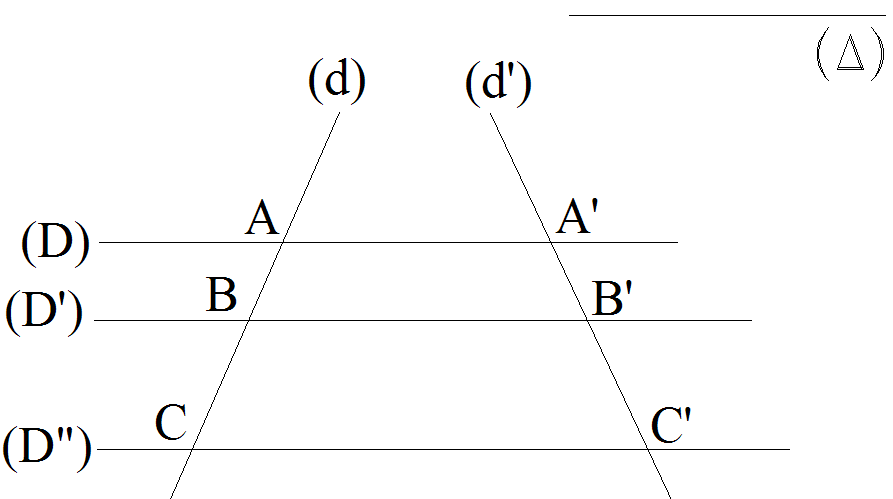
Soient A, B et C les points de rencontre de ces trois droites parallèles avec (d) et A', B' et C' leurs points de rencontre avec (d').
Si on considère la projection de (d) sur (d') selon la direction (D), alors l'image de A par cette projection sera A', celle de B sera B', celle de C sera C'.
On dira aussi que A et A' sont homologues dans la projection de (d) sur (d') selon la direction (D).
De même, B et B' sont homologues et C et C' le sont également.
Deux segments définis par des points homologues sont dits homologues.
Ainsi, A et A' étant homologues, B et B' l'étant aussi, [AB] et [A'B'] sont alors deux segments homologues.
Théorème 1
Si trois droites
parallèles (D), (D') et (D") rencontrent deux droites (d) et (d'),
respectivement et dans cet ordre,
en A, B, C et A', B', C', alors :
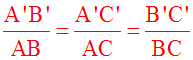
En d'autres termes :
Trois droites parallèles déterminent sur deux sécantes quelconques des segments homologues proportionnels.
Ce théorème est connu sous le nom de théorème de Thalès. En classe de Quatrième, il sera admis sans démonstration.
Cette proportion qui découle du
théorème de Thalès a des applications dans les domaines de
l’architecture, la topographie,
le dessin industriel et la mécanique classique.
Première conséquence
On sait qu'à partir d'une proportion, en permutant l'ordre des termes moyens ou extrêmes, on obtient une nouvelle proportion.
Ainsi,on a :
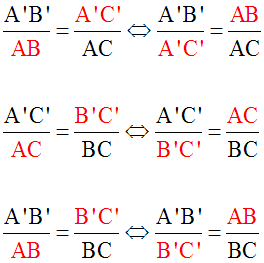
Le théorème de Thalès peut donc s'exprimer de la manière suivante :
Du fait du
parallélisme des trois droites (D), (D') et (D"), le rapport des
longueurs de deux segments quelconques pris sur une des
droites sécantes, par exemple (d'), est égal au rapport des
longueurs des deux segments homologues pris sur
l'autre, (d).
Une application directe à deux droites parallèles
Théorème 2
Si deux droites parallèles quelconques, (D) et (D'), rencontrent deux droites concourantes quelconques (d) et (d'), alors deux quelconques des segments définis sur (d) [resp. (d')] et les segments qui leur sont homologues, définis sur (d') [resp. (d)], sont dans une proportion.
Par ailleurs, (d) et (d') délimitent sur les droites parallèles (D) et (D') deux segments dont les longueurs sont dans une de ces proportions.
Démonstration
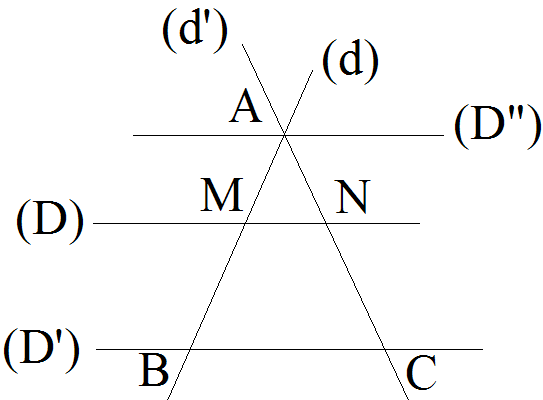
Soient deux droites concourantes quelconques (d) et (d') et soit A leur point d’intersection.
Soient (D) et (D') deux droites parallèles quelconques telles que :
(D) rencontre (d) et (d') respectivement aux points M et N
(D') rencontre (d) et (d') respectivement aux points B et C
Soit (D" ) la droite parallèle à (D) et (D') passant par A.
(D" ), (D) et (D') étant parallèles et coupées par les deux sécantes (d) et (d'), le théorème 1 s’applique : le rapport des longueurs de deux segments quelconques inclus dans (d) est égal à celui des longueurs des deux segments homologues inclus dans (d').
On a donc :
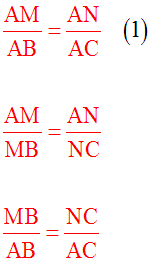
Dans chacune de ces proportions, en inversant les rapports, on obtient les trois autres proportions :
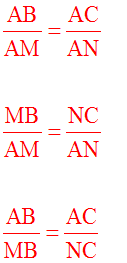
Démontrons la deuxième partie du théorème 2 qui énonce :" (d) et (d') délimitent sur les droites parallèles (D) et (D') deux segments dont les longueurs sont dans une de ces proportions."
Menons de N la droite parallèle à (AM) et rencontrant le côté [BC] au point P.
Le quadrilatère (MNPB) a, par construction et par hypothèse, ses côtés deux à deux opposés et parallèles ; donc (MNPB) est un parallélogramme.
Ses côtés opposés ont leurs longueurs égales ; donc MN = BP.
Soit (D1) la droite parallèle à (d) = (AM) et passant par C.
(D1), (NP) et (d) étant des droites parallèles coupées par les sécantes (d') et (D'), le théorème 1 s’applique : le rapport des longueurs de deux segments quelconques inclus dans (D') est égal à celui des longueurs des deux segments homologues inclus dans (d').
On a donc :
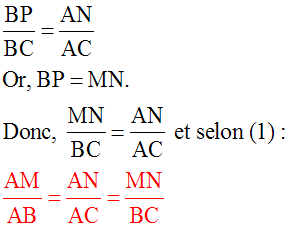
Remarque :
On aurait pu traiter le cas où (D) et (D') seraient de part et d'autre par rapport à (D"). Cependant, rien ne change pour ce qui est des démonstration et on obtiendra les mêmes résultats.
Une application directe à un trapèze
Dans un trapèze quelconque toute droite (d) parallèle aux bases partage les côtés non parallèles en des segments tels que, s’ils sont pris dans un ordre donné, ont leurs longueurs proportionnelles.
Démonstration
Soit (ABCD) un trapèze quelconque dont les bases sont [AB] et [DC].
Soit une droite (d) parallèle à ces bases et rencontrant les côtés non parallèles [AD] et [BC] respectivement en M et N.
Les droites (AB), (DC) et (d) étant trois droites parallèles coupées par les sécantes (AD) et (BC), le théorème 1 s’applique : deux segments quelconques définis sur (AD) et leurs homologues définis sur (BC) sont dans une proportion.
Ainsi, on a :

Théorème 3
Dans un triangle quelconque, le segment joignant les milieux de deux quelconques, de ses trois côtés, a son support parallèle à celui du troisième côté.
En Quatrième, ce théorème sera admis sans démonstration.
Conséquence qui en découle
Dans un triangle quelconque, le segment joignant les milieux
de deux quelconques, de ses trois côtés, a sa longueur égale à la
moitié de celle de ce troisième côté.
Démonstration
Dans un triangle (ABC), soient M et N milieux respectifs des côtés [AB] et [AC].
On a donc :
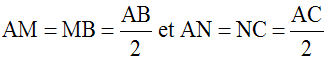
Or, d’après le troisième théorème ci-dessus, (MN) est parallèle à (BC).
(MN) étant parallèle à (BC), le théorème 1 s’applique : deux segments quelconques définis sur (AB) et leurs homologues définis sur (AC), sont dans une proportion.
De plus, la deuxième partie du théorème 2 s’applique : les segments [MN] et [BC] délimités par les sécantes (AB) et (AC) ont leurs longueurs dans une de ces proportions.
On a donc :
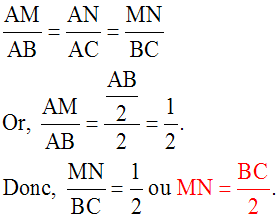
Théorème 4
Dans un triangle quelconque, si une droite passe par le milieu d’un, quelconque, de ses côtés, et est parallèle au support d’un second côté, alors elle passe par le milieu du troisième côté.
Démonstration
Dans un triangle (ABC), soit (d) une droite passant par le milieu M du côté [AB] et parallèle à(BC).
Soit N le point de rencontre de (d) avec le côté [AC].
(d) // (BC) ou encore (MN) // (BC); donc le théorème 1 appliqué au triangle (ABC) donne :
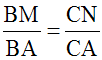

Parallélisme et proportionnalité - Applications à un triangle - Deuxième partie
3-
Je m’entraîneOn donne un triangle (ABC) et une droite (d) parallèle à [BC] rencontrant les côtés [AB] et [AC] respectivement aux points M et N.
AN = 6 cm ; NC = 2 cm ; MN = 4 cm.
Calcule BC.
Solution
(d) est parallèle à (BC) ; donc le
théorème 1 s’applique :
deux segments quelconques définis sur
(AB) et leurs homologues définis sur (AC) ont leurs longueurs
proportionnelles.
A a pour homologue lui-même, M a pour homologue N et B a pour homologue C.

Le théorème 2 complète cette proportion par la double proportion :
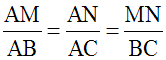

Dis pourquoi le triangle (ABC) tel que AB = 8 cm, AC = 6 cm et BC =5 cm existe.
Construis (ABC) avec ton compas et ta règle.
Sur [AB] place le point M tel que AM = 5 cm.
La parallèle à (BC) passant par M coupe le côté [AC] en N.
Calcule AN et MN.
Solution
8 – 5 < 6 < 8 + 5 ou AB – BC < AC < AB + BC
Les mesures des segments [AB], [BC] et [AC] vérifiant cette inégalité triangulaire, alors
le triangle (ABC) existe.
Pour construire (ABC), on procède de la manière suivante :
Avec la règle gradué, on construit un quelconque des trois segments [AB], [BC] et [AC], par exemple [AC].
Du point A, avec une ouverture de compas égale à 8 cm, on trace un arc de cercle (C1).
Du point C, avec une ouverture de compas égale à 5 cm, on trace un arc de cercle (C2).
(C1) et (C2) se coupent au point B.
On obtient ainsi le triangle (ABC) demandé.
Dans le triangle (ABC), (MN) étant
parallèle à (BC), support du côté [BC], le théorème 2
s’applique :
deux segments quelconques définis sur (AB) et
leurs homologues définis sur (AC)
ont leurs longueurs proportionnelles.
De plus, MN et BC sont dans une de ces proportions.
On a donc :
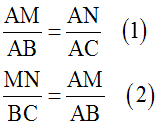
L’égalité (1) donne :
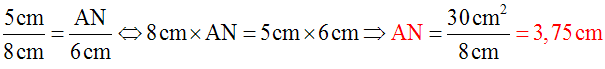
L’égalité (2) donne :
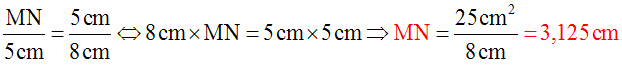
On donne deux droites (x’x) et (y’y) concourant au point O.
Sur (x’x), de part et d’autre de O, on place les points M et N tels que OM = 6 cm et ON = 12 cm.
Du point M, on trace une droite (d) coupant (y’y) au point M’.
Du point N, on mène la droite (d’) parallèle à (d) et rencontrant
(y’y) au point N’.
Sachant que OM’ = 1,5 cm, calcule ON’.
On pose MM’ = a ; calcule NN’ en fonction de a.
Solution
Les deux droites (d) et (d’) étant
parallèles, le théorème 2 s’applique :
deux segments
quelconques définis sur (x’x) et leurs homologues définis
sur (y’y) ont leurs longueurs proportionnelles.
De plus, (x’x) et (y’y) délimitent deux segments parallèles et dont les longueurs sont dans une de ces proportions.
Ainsi, on a :
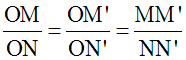
L’égalité des deux premiers rapports donne :
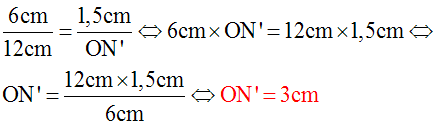
L’égalité du premier rapport et du troisième donne :
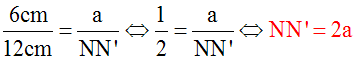
On donne un triangle quelconque (ABC).
Du point M milieu de [AB], on mène la droite (d) parallèle au support de [BC] et rencontrant [AC] au point N.
Du point N, on mène la droite (D) parallèle au support de [AB] et rencontrant [BC] au point P.
Démontre que [AP] est la médiane relative au côté [BC].
Solution
Dans le triangle (ABC), (d) passe par le milieu M du côté [AB] et est parallèle à au support du côté [BC].
Or, on sait que dans un triangle, si une droite passe par le milieu d’un côté et est parallèle au support d’un deuxième côté, alors elle passe par le milieu du troisième côté.
Par conséquent, (d) passe par le milieu du troisième côté [AC] qui ne peut être que N, puisque deux droites concourantes se rencontrent en un seul point.
Pour la même raison, (D) passant par le milieu N du côté [AC] et étant parallèle au support du côté [AB], passe par le milieu du troisième côté [BC] qui ne peut être que P.
P étant est milieu de [BC],
[AP] est la médiane relative au côté [BC].
On donne un triangle rectangle (ABC) dont l’angle droit est en A.
Soient M, N les milieux respectifs de [AB] et [AC].
On pose a la longueur de l’hypoténuse.
Calcule MN en fonction de a.
De N on mène la droite (d) parallèle à (AB) et rencontrant
l’hypoténuse au point P.
Quelle est la nature du quadrilatère (ANPM) ?

Solution
On sait que dans un triangle, le segment joignant les milieux de deux quelconques, de ses trois côtés, a son support parallèle à celui du troisième côté, et sa longueur égale à la moitié de celle de ce troisième côté.
Ainsi, [MN] joignant les milieux M et N des deux côtés [AB] et [AC], a son support parallèle à l’hypoténuse [BC] et sa longueur égale à la moitié de celle de cette hypoténuse ; donc :

Or, on sait que dans un triangle, si une droite passe par le milieu d’un côté et est parallèle au support d’un deuxième côté, alors elle passe par le milieu du troisième côté.
(d) passant par N milieu de [AC] et étant parallèle à (AB), passe donc par le milieu du troisième côté [BC] ; ainsi P est milieu de [BC].
M et P étant respectivement milieux de [BC] et [BA], le segment [PM] a son support parallèle à celui du troisième côté [AC].
Dans (ANPM), on a :
(NP) // (AB) ou (AM)
(PM) // (AC) ou (AN)
Ce quadrilatère, ayant les côtés deux à deux opposés et parallèles, est un parallélogramme.
De plus son angle au sommet A est droit ; donc il est
un rectangle.On sait que dans un rectangle, les diagonales ont leurs longueurs égales ; donc, dans le rectangle (ANPM), AP = MN.
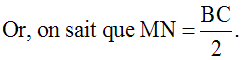
Deux quantités égales à une même troisième sont égales ; par conséquent :
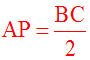
Remarque importante
P étant milieu de [BC], donc [AP] étant la médiane relative à l’hypoténuse [BC], on vient de démontrer une propriété importante de tout triangle rectangle :
La longueur de la médiane relative à l’hypoténuse est égale à la moitié de la longueur de cette hypoténuse.
On donne un triangle quelconque (ABC).
On trace une droite (d) parallèle à (BC), rencontrant [AC] et [AB]
respectivement aux points M et E.
On trace une droite (d’) passant par E, parallèle à (AC) et rencontrant [BC] au point K.
Complète :
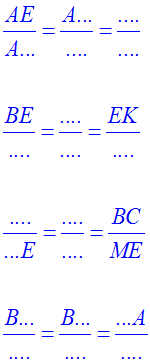
Solution
(d) ou (EM) est parallèle au support du côté [BC] ; donc le théorème 2 s’applique : deux segments quelconques définis sur (AB) et leurs homologues définis sur (AC) ont leurs longueurs proportionnelles.
De plus les segments [EM] et [BC] ont leurs longueurs dans une de ces proportions.
Ainsi, M et E étant homologues, on a :
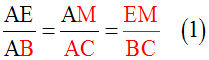
(d’) ou (EK) est parallèle au support du côté [AC] ; donc le théorème 2 s’applique : deux segments quelconques définis sur (AB) et leurs homologues définis sur (BC) ont leurs longueurs proportionnelles.
De plus les segments [EK] et [AC] ont leurs longueurs dans une de ces proportions.
Ainsi, E étant homologue de K, on a :
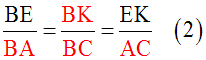
Si on inverse les rapports dans la double proportion (1), on obtient la double proportion :
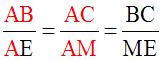
Si on inverse les rapports dans la double proportion (2), on obtient la double proportion :
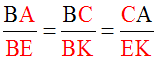
On donne deux droites concourantes (D1) et (D2) et O leur intersection.
(d) et (d’) sont deux droites parallèles telles que :
- (d) et (d’) coupent (D1) respectivement aux points A1 et B1
- (d) et (d’) coupent (D2) respectivement aux points A2 et B2
On a :
A1B1 = 3 cm; OB1 = 5 cm et OB2 = 4 cm
Calcule A2B2
Solution
Les deux droites parallèles (d) et (d’) étant parallèles, le théorème 1 s’applique : deux segments quelconques définis sur (D1) et leurs homologues définis sur (D2) ont leurs longueurs proportionnelles.
Ainsi, par exemple :
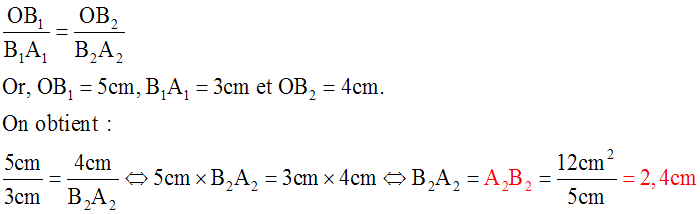
On donne un
jardin trapézoïdal (ABCD) dont la petite base est [AB] et dont la hauteur mesure h = 7 m.Les droites contenant les côtés non parallèles se coupent au point O.
Sachant que OA = 15 m, AD = 10 m, CD = 35 m, calcule AB et en déduire l’aire de ce jardin en ares.
Solution
Dans le triangle (ODC), la droite (AB) est parallèle à (DC), support du côté [DC].
Par conséquent, le deuxième théorème s’applique : deux segments quelconques définis sur (OD) et leurs homologues définis sur (OC) ont leurs longueurs proportionnelles.
De plus, [AB] et [DC] ont leurs longueurs dans une de ces proportions.
Ainsi, on a :
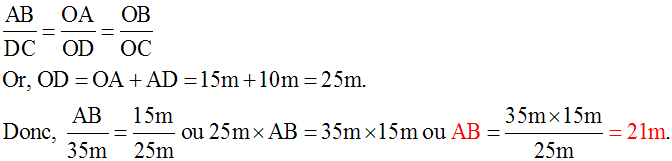
Si on pose S l’aire du jardin, et sachant
que l’aire d’un trapèze est égale au produit de sa hauteur par la
demi somme
de ses bases, alors :
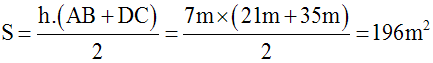
Or, on sait que 1 are vaut 1 dam 2
Donc S = 1,96 dam 2 = 1, 96 ares.
Parallélisme et proportionnalité - Applications au triangle - Troisième partie
On donne un triangle quelconque (ABC).
Soit B’ un point quelconque appartenant au côté [AB].
On mène de B’ la droite (d) parallèle à (BC) qui coupe le côté [AC] au point C’.

1- Dans le triangle (ABC), on abaisse de A la hauteur [AH]
relative au côté [BC] qui rencontre (d) en H’.
Démontre que dans le
triangle (AB’C’), [AH’] est la hauteur relative au côté [B’C’].

P et P’ étant les périmètres respectifs des triangles (ABC) et (AB’C’) ;
S et S’ étant leurs aires respectives,
démontre que :
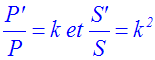
2- Dans le triangle (ABC), on mène la médiane [AM] relative au côté [BC]. Elle coupe (d) au point M’.
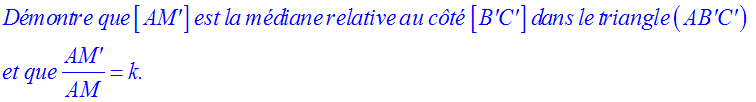
Solution
1-
(AH) étant perpendiculaire à (BC), elle est
perpendiculaire à toute droite parallèle à (BC) et en particulier à
(d).
Comme H’ appartient à (AH), (AH) et (AH’) sont identiques.
Par conséquent (AH’) est perpendiculaire à (d) ou encore à (B’C’) ; ainsi
[AH’] est la hauteur relative au côté [B’C’]dans le triangle (AB’C’).
Dans le triangle (ABH), la droite (B’H’) est parallèle au support de [BH], car (d) et (BC) sont parallèles.
Par conséquent, le premier théorème s’applique : deux segments quelconques définis sur (AB) et leurs homologues définis sur (AH) ont leurs longueurs proportionnelles.
Ainsi, on a :
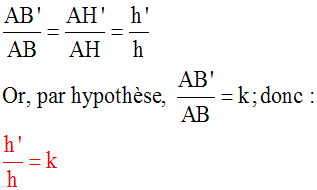
P est égal à la somme des trois longueurs des côtés du triangle (ABC) ; donc :
P = AB + BC + CA
P’ étant le périmètre du triangle (AB’C’), on a :
P’ = AB’ +B’C’+C’A
Or, dans le triangle (ABC), (B’C’) étant parallèle à (BC), le théorème 2 s’applique : deux segments quelconques définis sur (AB) et leurs homologues définis sur (AC) ont leurs longueurs proportionnelles.
De plus, [B’C’] et [BC] ont leurs longueurs dans une de ces proportions.
Ainsi, on a :
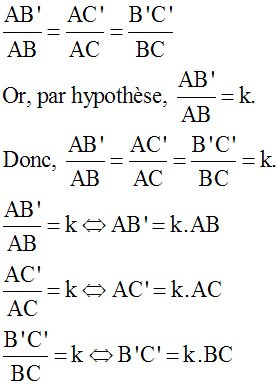
En additionnant membre à membre les trois dernières égalités ci-dessus, on obtient :
P’ = AB’ + AC’ + B’C’ = k . AB + k . AC + k . BC =
k . (AB + AC + BC)
Or, AB + AC + BC = P
Donc finalement :
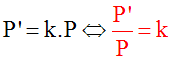
S étant l’aire du triangle (ABC), on a :
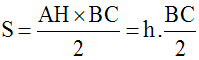
S’ étant l’aire du triangle (AB’C’), on a :
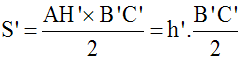
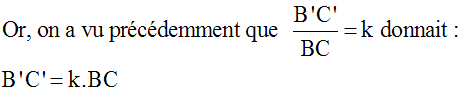
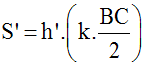
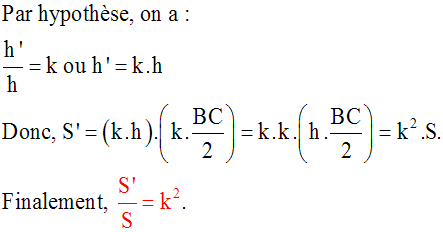
2-
Dans le triangle (ABM), la droite (B’M’) est parallèle au support de [BM], car (d) et (BC) sont parallèles.
Par conséquent, le deuxième théorème s’applique : deux segments quelconques définis sur (AB) et leurs homologues définis sur (AM) ont leurs longueurs proportionnelles.
De plus, [B’M’] et [BM] ont leurs longueurs dans une de ces proportions.
Ainsi, on a :
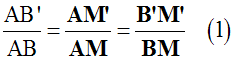
Dans le triangle (AMC), la droite (M’C’) est parallèle au support de [MC], car (d) et (BC) sont parallèles.
Par conséquent, le deuxième théorème s’applique : deux segments quelconques définis sur (AC) et leurs homologues définis sur (AM) ont leurs longueurs proportionnelles.
De plus, [M’C’] et [MC] ont leurs longueurs dans une de ces proportions.
Ainsi, on a :
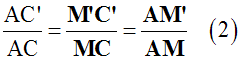
Sachant que deux quantités égales à une même troisième sont égales, les deux dernières proportions (1) et (2) donnent :
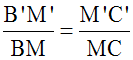
Or, on sait que dans une proportion, si on permute les termes moyens (ou les termes extrêmes), on obtient une nouvelle proportion.

Or, par hypothèse, on a dans le triangle (ABC), [AM] médiane relative au côté [BC] ; donc M est milieu de [BC] ;
ainsi MB = MC.
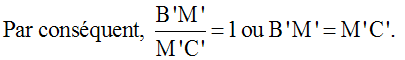
Ceci traduit que M’ est milieu du côté [B’C’], ou encore que
[AM’] est la médiane relative à [B’C’], dans le triangle (AB’C’).
Par ailleurs, on a vu précédemment que :
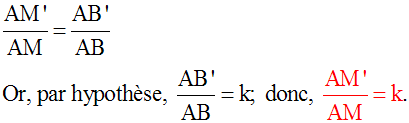
On donne un triangle quelconque (ABC) dont les côtés [AB], [BC] et [AC] ont respectivement pour longueurs c, a et b, et dont la hauteur relative au côté [BC] a pour pied H et pour longueur h.
Un point M se déplace sur le côté [AB]. On pose x la longueur AM.
Dans quel intervalle de nombres varie x ?
1ère partie
On donne deux nombres positifs a et b.
Calcule ( a + b) et ( a . b) dans chacun des cas suivants :
a = 1 et b = 7
a = 2 et b = 6
a = 3 et b = 5
a = 4 et b = 4
a = 5 et b = 3
a = 6 et b = 2
a = 7 et b = 1
Que constates-tu ?
On donne deux autres nombres positifs m et n.
Calcule ( m + n) et (m . n) dans chacun des cas suivants :
m = 1 et n = 15
m = 2 et n = 14
m = 3 et n = 13
m = 4 et n = 12
m = 5 et n = 11
m = 6 et n = 10
m = 7 et n = 9
m = 8 et n = 8
m = 9 et n = 7
m = 10 et n = 6
m = 11 et n = 5
m = 12 et n = 4
m = 13 et n = 3
m = 14 et n = 2
m = 15 et n = 1
Que constates-tu encore ?
Énonce la propriété obtenue.
On admettra cette propriété pour la suite de l’exercice.
2ème partie
De M on trace la droite (d) parallèle à (BC) qui rencontrera le côté [AC] au point N. De N on trace la droite (D) parallèle (AB) qui rencontrera le côté [BC] au point P.
Quelle est la nature du quadrilatère (MNPB) ?
Calcule en fonction de a, b, c, h et x le périmètre et l’aire de ce quadrilatère.
Pour quelle valeur de x l’aire de (MNPB) est-elle maximum ? Quelle est dans ce cas la position de M ? Calcule ce maximum ; que constates-tu ?
Solution
M se déplace tout en restant sur [AB] ; donc il a deux positions limites : lorsqu’il se confond avec A, dans ce cas AM ou x est nulle et lorsqu’il se confond avec B, dans ce cas AM ou x vaut AB = c.
x
devant rester largement positive, varie donc dans l’intervalle [0 ; c].
1ère partie
(a + b) et (a . b) prennent respectivement les valeurs :
8 et 7 ; 8 et 12 ; 8 et 15 ; 8 et
16 ; 8 et 15 ; 8 et 12 ; 8 et 7.La somme (a + b) restant
constante, le produit (a . b) croît de 7 à 16 puis décroît de 16 à 7.De plus, ce produit atteint son
maximum qui est 16 pour a = b = 4.(m + n) et (m . n) prennent respectivement les valeurs :
16 et 15 ; 16 et 28 ; 16 et 39 ; 16 et 48 ; 16 et 55 ; 16 et 60 ; 16 et 63 ; 16 et
64 ; 16 et 63 ; 16 et 60 ; 16 et 55 ; 16 et 48 ; 16 et 39 ; 16 et 28 ; 16 et 15.La somme (m + n) restant
constante, le produit (m . n) croît de 15 à 64 puis décroît de 64 à 15.De plus, ce produit atteint son
maximum qui est 64 pour m = n = 8.Conclusion
Si deux nombres positifs varient de manière que leur somme reste constante, leur produit varie et atteindra son maximum lorsque ces deux nombres deviennent égaux.
Pour la suite, on admettra cette propriété.
2ème partie
Par construction, (MN)
et (BC) ou (BP) sont parallèles ; il en est de même pour (NP) et (AB) ou (MB).(MNPB)
, ayant ainsi ces côtés deux à deux opposés et de supports parallèles, est un parallélogramme.On pose P le périmètre de (MNPB). On a donc :
P = MN + NP + PB + BM
Comme aussi dans un
parallélogramme les côtés opposés ont même longueur, MN
= BP et MB = NP et
P = MN + MN + BM + BM = 2MN + 2BM = 2(MN + BM).
Dans le triangle (ABC), la droite (MN) est parallèle au support du côté [BC] ; par conséquent, le deuxième théorème s’applique : deux segments quelconques définis sur (AB) et leurs homologues définis sur (AC) ont leurs longueurs proportionnelles.
De plus, [MN] et [BC] ont leurs longueurs dans une de ces proportions.
Ainsi, on a la double proportion :
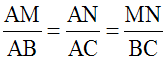
L’égalité du premier rapport et du dernier donne la proportion :
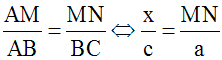
Sachant que dans une proportion, le produit des termes extrêmes est égal à celui des termes moyens, on a :

MB = AB – AM = c – x
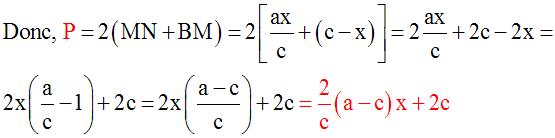
On pose S l’aire de (MNPB).
Soit H’ l’intersection de la hauteur [AH] avec (MN).
On sait que l’aire d’un parallélogramme est le produit de la longueur d’une quelconque de ses dimensions par la longueur de la hauteur correspondante.
Ainsi S = MN . HH’
Dans le triangle (ABH), la droite (MH’) étant parallèle au support de [BH], le premier théorème s’applique : deux segments quelconques définis sur (AB) et leurs homologues définis sur (AH) ont leurs longueurs proportionnelles.
Ainsi, on a une de ces proportions :
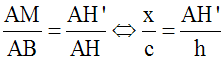
Sachant que dans une proportion, le produit des termes extrêmes est égal à celui des termes moyens, on a :
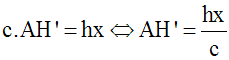

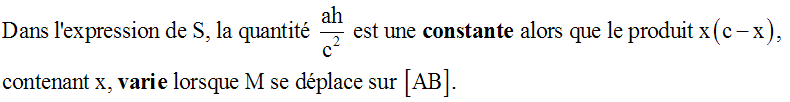
Or, on a :
x ≥ 0
et AB ≥ AM ou AB – AM ≥ 0 ou c – x ≥ 0x + (c – x) = x + c – x = c et c est une constante.
Les quantités positives x et (c – x) varient de manière que leur somme reste constante.
Selon la propriété obtenue dans la première partie de cet exercice, leur produit, variant avec x, atteindra son maximum lorsqu’elles deviennent égales, c’est-à-dire lorsque x = c – x.
Donc, S atteindra son maximum lorsque x = c – x.
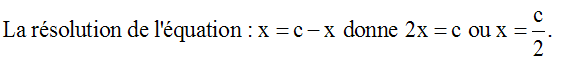
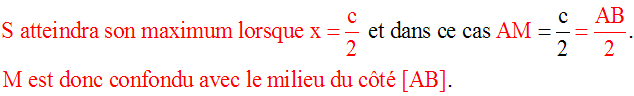

On donne un triangle quelconque (ABC). On suppose
l'angle au sommet A aigu.
La bissectrice
[Ax de l’angle intérieur au sommet A rencontre le côté
[BC], opposé à A, au point M.
[Ax sera appelée bissectrice intérieure en A.
Du point C on mène la demi-droite [Cy parallèle à (AM) ; cette demi-droite rencontre (BA) au point F.
Démontre que le triangle (AFC) est isocèle.

Dans un triangle, on appelle
angle extérieur tout angle adjacent et supplémentaire à un angle intérieur.Ainsi, l’angle {[AC) , [AF)} est un angle extérieur car il est adjacent et supplémentaire à l’angle intérieur au sommet A.
Soit [At la bissectrice de {[AC) , [AF)}.
[At sera appelée bissectrice extérieure en A.
[At rencontre (BC) au point N.
Démontre la double proportion :
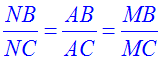
Quelle propriété peux-tu alors en déduire pour un triangle ?
Solution
(AM) et (CF) sont deux droites parallèles coupées par la sécante (AC) ; or, on sait que, dans ce cas, les angles alternes internes ont même mesure.
Par ailleurs, ces deux droites parallèles, coupées par la sécante (BA), définissent avec celle-ci des angles correspondants de même mesure.
Donc, les angles alternes internes {[CA) , [CF)} et
{[AM) , [AC)} ont même mesure.Et aussi les angles correspondants {[FA) , [FC)} et {[AB) , [AM)} ont même mesure.
Or [Ax étant la bissectrice de l’angle intérieur au sommet A, les angles {[AM) , [AC)} et {[AB) , [AM)} ont même mesure.
Deux quantités égales à une même troisième sont égales ; par conséquent,
{[CA) , [CF)}et {[FA) , [FC)} ont même mesure et le triangle (AFC) est isocèle.
Dans le triangle (BCF), la droite (AM) est parallèle au support du côté [CF]. Par conséquent, le premier théorème s’applique :
deux segments quelconques définis sur (BC) et leurs homologues définis sur (BF) ont leurs longueurs proportionnelles.
Ainsi, on a une de ces proportions :
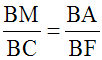
On connaît une des propriétés d'une proportion quelconque :
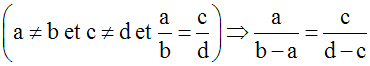

Or, le triangle (AFC) étant isocèle, ses côtés [AC] et [AF] ont même mesure ; donc AC = AF.
En remplaçant AF par son égale AC, dans la dernière proportion ci-dessus, on obtient :
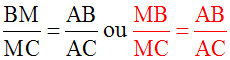
Dans un triangle quelconque, toute bissectrice
intérieure partage le côté qui lui est opposé en deux
segments.
Ces derniers et les deux autres côtés ont
leurs longueurs dans une proportion.
Soit (d) la droite passant par C et parallèle à (AN). Elle coupe (BA) au point E.
(AN) et (EC) sont deux droites parallèles coupées par la sécante (AC) ; or, on sait que, dans ce cas, les angles alternes internes ont même mesure.
Par ailleurs, ces deux droites parallèles, coupées par la sécante (AE), définissent avec celle-ci des angles correspondants de même mesure.
Donc, les angles alternes internes {[CA) , [CE)} et
{[AC) , [At)} ont même mesure.Et aussi les angles correspondants {[EA) , [EC)} et {[AF) , [At)} ont même mesure.
Or [At étant la bissectrice de l’angle extérieur {[AC) , [AF)}, les angles {[AC) , [At)} et {[AF) , [At)} ont même mesure.
Deux quantités égales à une même troisième sont égales ; par conséquent,
{[CA) , [CE)}et {[EA) , [EC)} ont même mesure et le triangle (AEC) est isocèle.
Dans le triangle (BAN), la droite (EC) est parallèle au support du côté [AN]. Par conséquent, le premier théorème s’applique :
deux segments quelconques définis sur (BA) et leurs homologues définis sur (BN) ont leurs longueurs proportionnelles.
Ainsi, on a une de ces proportions :
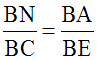
Par application d’une propriété des proportions, on obtient :
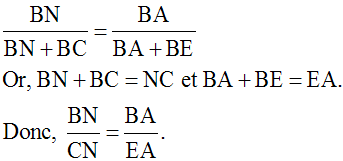
Or, le triangle (AEC) étant isocèle, ses côtés [AC] et [EA] ont même mesure ; donc AC = EA.
En remplaçant EA par son égale AC, dans la dernière proportion ci-dessus, on obtient :
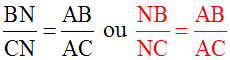
Dans un triangle quelconque, toute bissectrice
extérieure partage le côté qui lui est opposé en deux
segments.
Ces derniers et les deux autres côtés ont
leurs longueurs dans une proportion.
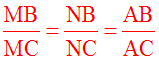
Dans un triangle quelconque, les bissectrices intérieure et extérieure menées d’un sommet quelconque partagent le côté qui leur est opposé en des segments. Ces derniers et les deux autres côtés, pris dans un ordre donné, ont leurs longueurs dans une double proportion.
On te donne un triangle (ABC) avec AB = 3 cm et AC = 5 cm.
La bissectrice de l’angle intérieur au sommet A coupe le côté opposé [BC] au point M tel que MB = 2 cm.
Calcule la longueur de [BC].
Solution
On sait que la bissectrice intérieure en A partage le côté opposé [BC] en deux segments [MB] et [MC] tels que :
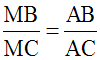
Ainsi, on a :
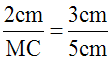
Dans une proportion, le produit des termes extrêmes est égal à celui des termes moyens ; donc :
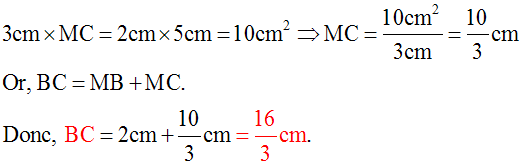
Anna se trouve en randonnée dans les Alpes.
Elle est sur un terrain assez plat, face à un arbre.
Elle souhaite connaître la hauteur h de cet arbre, sans prendre le risque en grimpant.
Les outils qu’elle possède est une boussole, un canif et un double décamètre.
Comment a-t-elle procédé pour trouver h ?
Solution
Avec son canif, elle se fabrique un bâton suffisamment droit de 150 cm de longueur, ceci à l’aide d’une petite branche d’arbre.
Elle plante au sol et verticalement ce bâton à la distance de 200 mètres du pied Q de l’arbre.
Elle nomme P le pied de son bâton, S et R les sommets respectifs de l’arbre et de son bâton.
Le bâton ainsi planté, Anna s’allonge sur l’herbe tout en fixant le sommet R du bâton, et tout en rampant jusqu’à ce qu’elle obtienne, à l’œil nu, une visée permettant de constater l’alignement de son œil O, avec R et S, O étant le plus proche possible du sol.
Dans cette position, elle se procure une petite pierre qu’elle pose à l’endroit O’ où se trouve sa tête, O’ étant sur la verticale passant par son œil.
O étant le plus proche possible du sol, Anna considère alors que O’ et O sont pratiquement confondus.
Elle se lève, puis avec son double décamètre, elle mesure la longueur O’P.
Elle trouve O’P = 5 mètres.
Elle procède ensuite au raisonnement suivant : "
Dans le triangle (O’QS), (PR) est une droite parallèle au support (QS) du côté [QS], car (PR) et (QS) sont des verticales.
Donc, deux segments quelconques définis sur (O’S) et leurs homologues définis sur (O’Q) ont leurs longueurs proportionnelles.
De plus, le segment [PR] et le côté [QS] ont leurs longueurs dans une de ces proportions.
Je peux donc écrire :
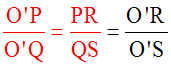
Or, je sais que O’Q = O’P + PQ = 5m + 200m = 205m.
Dans la première proportion que je viens d’écrire, je remplace O’P, O’Q et PR par leurs valeurs que je connais ; j’obtiens :
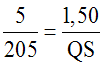
Je sais que dans une proportion, le produit des termes extrêmes est égal à celui des termes moyens ; donc :
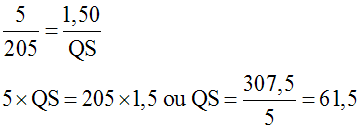
Or, QS est la hauteur h de cet arbre ; donc je trouve :
h = 61,5 mètres. "
3,4,5,......Pythagore - 2ème partie
L’outil le plus fréquent utilisé dans les exercices et les problèmes est la réciproque de ce théorème qui s’énonce comme suit :
Dans un triangle, si le carré de la longueur d’un de ses côtés est égal à la somme des carrés des longueurs des autres côtés, alors ce triangle est un triangle rectangle.
Je la démontre.
Je considère un triangle (ABC) tel que :
BC2 = AB2 + AC2
Je mène de
C (j’aurai pu le faire également de B) la hauteur
relative au côté [AB] qui rencontre
(AB) en A’.
Deux cas de figure peuvent se présenter : A’ appartient à [AB] ou A’ n’appartient pas à [AB].
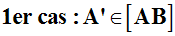
Le théorème de Pythagore appliqué au triangle (CA’B) rectangle en A’ donne :
BC2 = A’B2 + A’C2 (3)
Mais aussi, le même théorème appliqué au triangle (CA’A) rectangle en A’, donne :
AC2 = A’A2 + A’C2 (4)
Or, par hypothèse, j’ai :
BC2 = AB2 + AC2
Dans l’égalité (3), je remplace BC2 par son égal AB2 + AC2 ; j’obtiens :
AB2 + AC2 = A’B2 + A’C2 (5)
Dans l’égalité (5), je remplace AC2 par son égal A’A2 + A’C2 ; j’obtiens :
AB2 + A’A2 + A’C2 = A’B2 + A’C2
En simplifiant par A’C2 , j’obtiens :
AB2 + A’A2 = A’B2 (6)
Or, A’ appartenant à [AB], j’ai donc, en utilisant l'égalité remarquable,
(X – Y)2 = (X – Y) (X – Y) = X2 – 2XY + Y2 :
A’B = AB – AA’ et ainsi, A’B2 = AB2 + AA’2 – 2AB.AA’
En remplaçant dans (6), A’B2 par son égale :
AB2 + AA’2 – 2AB.AA’
j’obtiens :
AB2 + A’A2 = AB2 + AA’2 – 2AB.AA’ ou encore, après simplification :
0 = – 2AB.AA’
En simplifiant par AB différente de zéro, j’obtiens :
0 = – 2AA’

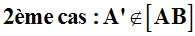
Le théorème de Pythagore appliqué au triangle (CA’B) rectangle en A’ donne :
BC2 = A’B2 + A’C2 (3’)
Mais aussi, le même théorème appliqué au triangle (CA’A) rectangle en A’, donne :
AC2 = A’A2 + A’C2 (4’)
Or, par hypothèse, j’ai :
BC2 = AB2 + AC2
Dans l’égalité (3’), je remplace BC2 par son égal AB2 + AC2 ; j’obtiens :
AB2 + AC2 = A’B2 + A’C2 (5’)
Dans l’égalité (5’), je remplace AC2 par son égal A’A2 + A’C2 ; j’obtiens :
AB2 + A’A2 + A’C2 = A’B2 + A’C2
En simplifiant par A’C2 , j’obtiens :
AB2 + A’A2 = A’B2 (6’)
Or, A’ n’appartenant pas à [AB], j’ai donc, en utilisant l'égalité remarquable,
(X + Y)2 = (X + Y) (X + Y) = X2 + 2XY + Y2 :
A’B = AB + AA’ et ainsi, A’B2 = AB2 + AA’2 + 2AB.AA’
En remplaçant dans (6’), A’B2 par son égale :
AB2 + AA’2 + 2AB.AA’
J’obtiens :
AB2 + A’A2 = AB2 + AA’2 + 2AB.AA’ ou encore, après simplification :
0 = 2AB.AA’
En simplifiant par AB différente de zéro, j’obtiens :
0 = 2AA’

Conclusion :

La réciproque du théorème de Pythagore est ainsi
démontrée.
Maïssane, collégienne hors du commun
Maïssane a su, à l'aide d'un chevron parfaitement
droit, calculer à quelle hauteur du sol se trouve le
centre d'une plaque d''inscription encastrée sur un mur
vertical.
Comment a-t-elle procédé ?
La donnée du problème : la longueur du chevron est
supérieure à la hauteur recherchée.
Solution
Maïssane peut facilement mesurer la longueur du chevron;
elle trouve L.
Ensuite, elle appuie ce chevron au mur de manière à ce
que son sommet vienne toucher, en équilibre, le
centre de la plaque.
Elle procède à la mesure de la distance qui sépare le
pied du mur de celui du chevron; elle trouve d.
L
et d étant connues et sachant que le mur est
vertical et que le sol est horizontal, elle
applique le théorème de Pythagore au triangle formé par
le sommet du chevron appuyé au mur, son pied au sol et
le pied du mur.
Elle écrit alors :
X2
+ d2 = L2, X étant la hauteur à
laquelle se trouve le centre de la plaque par rapport au
sol.
Ce
qui donne finalement :
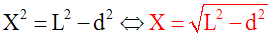
Inéquations - Première partie
Bien qu’il soit dédié à la Troisième, ce chapitre peut être un outil de révision pour un élève de Seconde, ayant eu des difficultés lors de l’étude des inéquations
Inéquations
1- Inégalité et propriétés
1-1- Inégalité
Soient deux nombres réels quelconques a et b.
On dira que a et b sont comparables lorsqu’au moins une des relations :

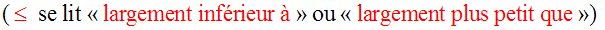
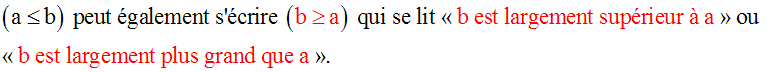
Cette relation, dite « inégalité large », est
partout définie dans R.
Ceci veut dire que pour
tout a réel et pour tout b réel, a et b sont comparables.
Propriétés
Pour tous a, b, c réels :
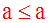
On dit que l’inégalité est réflexive.
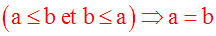
On dit que l’inégalité est antisymétrique.
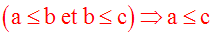
On dit que
l’inégalité est transitive.
On conclut en disant que l’inégalité est une relation d’ordre partout définie dans R.
On ne change pas le sens de l’inégalité en additionnant à ses deux membres une même quantité :
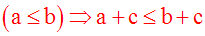
On
ne change pas le sens de l’inégalité en multipliant ses deux membres par une
quantité positive :
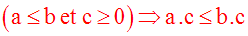
Soient deux nombres réels quelconques a et b.
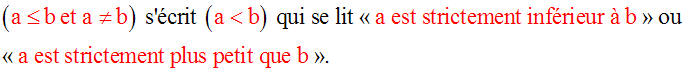
On aura ainsi défini l’inégalité stricte.
On peut écrire indifféremment :
a < b ou b > a
Cette dernière écriture se lit « b est
strictement supérieur à a » ou « b
est strictement plus grand que a ».
Pour tout
réel a, (a < a) est
fausse.
Donc l’inégalité
stricte n’est pas partout définie
dans R.
Propriétés
L’inégalité stricte est transitive.
Pour tous a, b, c réels
(a > 0 et b > 0 et a > b et c > 0) implique c.a > c.b
Exemple :
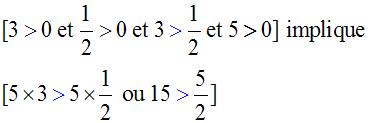
(a > 0 et b > 0 et a > b et c < 0) implique c.a < c.b
Exemple :
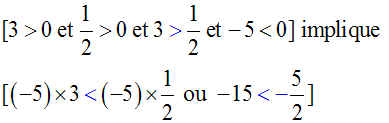
(a < 0 et b < 0 et a > b et c > 0) implique a.c > b.c
Exemple :

(a < 0 et b < 0 et a > b et c < 0) implique a.c < b.c
Exemple :
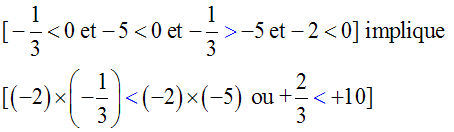
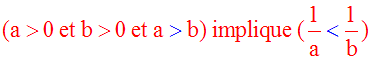
Exemple :

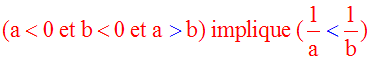
Exemple :
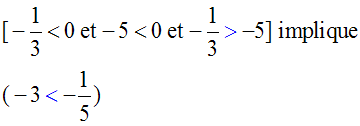
2- Inéquation à une inconnue, du premier degré par à son inconnue
2-1- Définitions
x + 5 = x1 + 5 > 0 est une inéquation dont l’inconnue est x. Le plus grand exposant de x étant 1, elle sera dite du premier degré par rapport à x.
y2 – 5y < 1 est une inéquation dont l’inconnue est y. Le plus grand exposant de y étant 2, elle sera dite du second degré par rapport à y.
Soient a et b deux nombres réels quelconques
.
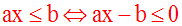
En effet, en ajoutant aux deux membres de la première
inéquation une même quantité (– b), on obtient :
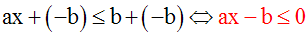
De même on a :
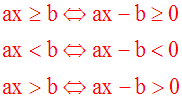
Conclusion :
Toute inéquation à une inconnue du premier degré par rapport à cette inconnue peut se mettre sous une des formes générales :
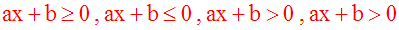
a, b seront appelés coefficients de l’inéquation.