GESTION DE MATHS FLASH (19)

Cette page sera enrichie en permanence; je te conseille donc de la visiter régulièrement
 
 
 
Les expressions ou énoncés qui suivent nous font sûrement perdre des points à l'épreuve de mathématiques, à savoir :

 

 

Simplifions par A(x)

Ici on a oublié de préciser que la simplification n'est possible que si A est différent de 0.

 
 
 

 

 

 

 

 

La primitive de f est F

f possède à une constante près une infinité de primitives; donc à la place de l'article " La " on devait écrire  " Une ".
 

 

 

 

 

 

 

 


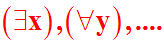
Pour exprimer que quel que soit y, il existe au moins x on a écrit " il existe au moins x tel que quel que soit y "

Ce n'est pas du tout pareil; en effet dans l'expression " que quel que soit y, il existe au moins x " les éléments x peuvent être nombreux à satisfaire les propriétés ou conditions qui suivent, alors que dans l'expression "  il existe au moins x tel que quel que soit y " x est unique pour tous les éléments y.

 

 

 

 

 

 

 

 

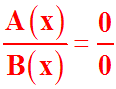
Dans des cas où des formes indéterminées interviennent, il est souhaitable de rédiger des phrases telle que :

Le rapport ci-dessus, lorsque x tend vers..., prend une forme indéterminée; levons cette indétermination...
 
 
 
 
 

 

 

 

 

f étant continue en tout point x appartenant à l'intervalle [a,b], elle est continue sur cet intervalle.

 
Pour que f soit continue sur un intervalle [a,b] il suffit :

1- qu'elle soit continue sur l'intervalle ouvert ]a,b[

2- qu'elle soit continue à droite au point a et continue à gauche au point b, c'est-à-dire
la limite de f(x) lorsque x tend vers a par valeurs supérieures soit égale à f(a) et la limite de f(x) lorsque x tend vers b par valeurs inférieures soit égale à f(b)

Ainsi, la phrase écrite ci-dessus manque de rigueur; il est souhaitable de la remplacer par celle qui suit :

f étant continue sur ]a,b[, continue à droite au point a, continue à gauche au point b, elle est continue sur [a,b].
 
 
 
 
 

 

 

 

 

f étant continue au point a, elle est dérivable en ce point.

 
Cette phrase est une erreur très grave; en effet la réciproque du théorème :
f étant dérivable au point a, elle est continue en ce point est fausse.
 
 

 

 

 

 

 

 
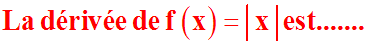
L'erreur est de se lancer immédiatement dans le calcul de l'expression de la dérivée, sans ce soucier de l'expression sous valeur absolue (ici, x).

Si x est largement positive, f(x) est égale à x et si x est strictement négative, f(x) est égale à -x.
 

Ainsi, la dérivée est égale à 1 si x est largement positive et à - 1 si x est strictement négative.
 
 
 
 
 

 

 

 

 
 
D'après ce qui précède, f possède au point 0 deux dérivées, à gauche et à droite, différentes ( - 1 différent de 1); donc f n'est pas dérivable au point 0.
 
 
 
 
 

 

 

f(x) = x2



Ne jamais oublier le symbole dx, sous le signe de la somme. On devait donc écrire :



 
 

 

 

 

 

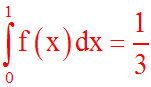
t variable indépendante


u(t) = f[x(t)] implique u ' = f ' [x(t)]
 
u est une fonction de fonction; sa dérivée (par rapport à t) est égale au produit de la dérivée de f par rapport à x par la dérivée de x par rapport à t.

Donc u ' (par rapport à t) = f ' (par rapport à x) . x ' (par rapport à t)
 
Exemple :
 
u(t) = f[x(t)], avec x(t) = 2t2 et f(x) = x3

f ' (par rapport à x) est 3x2
 

x ' (par rapport à t) est 4t


 u '(t) = 3x2 . [4t] = 3[2t2]2 . (4t) = 12t4 . 4t = 48t5

 

 
 
 
 

 

 

La limite de f(x) lorsque x tend vers a par valeurs inférieures étant égale à la limite de f(x) lorsque x tend vers a par valeurs supérieures, f est donc continue au point a.

 
la condition d'égalité des deux limites de f(x), à gauche et à droite de a, n'est pas une condition suffisante pour la continuité de f au point a.

A cette condition il faudra ajouter celle exprimant que ces deux limites doivent avoir f(a) comme valeur commune, a étant évidemment un élément appartenant au domaine de définition de f.

On devait donc écrire :

Les limites de f(x) lorsque x tend vers a par valeurs inférieures et lorsque x tend vers a par valeurs supérieures sont toutes deux égales à f(a); f est donc continue au point a.

Exemple :

On te donne la fonction numérique définie par :

f(x) = x, si x est différent de 3

f(3) = - 2

Démontre que f n'est pas continue au point 3.

 

 

 

 

 

 

(x - 3) (x + 1) = 0 logiquement équivalente à x - 3 = 0  et  x + 1 = 0 logiquement équivalente à x = 3  et x = - 1

x ne peut être simultanément égal à 3 et - 1; donc la conjonction " et " devra être remplacée par la disjonction inclusive " ou ".

D'une manière générale on écrit :
 

A . B = 0 logiquement équivalente à A = 0  ou  B = 0
 

 

 

 

 

 

 

Arc sin (- 1, 1002)

Des résultats d'un calcul numérique tels que Arc sin (a) ou Arc cos (a), avec a strictement inférieure à - 1 ou strictement supérieure à + 1 sont tous faux.

En effet, Arc sin (a) veut dire " Arc dont le sinus est a ". Mais comme le sinus est toujours largement compris entre - 1 et +1, la valeur de a ne peut être ni strictement supérieure à + 1 , ni strictement inférieure à - 1.
 

Il en est de même pour Arc cos (a).
 
 
 
 

 

 

 
– 2x

La fonction numérique  f(x) = ax  dite " fonction puissance " n'est définie que pour a réel strictement positif.

En effet, ax peut également s'écrire e[x . Log(a)]  et ainsi le réel Log(a) n'est défini que pour a strictement positif.

 

 

 

 

 

 

 

u fonction numérique

[u(x)n] ' = n . [u(x)(n – 1)]
 
Cette formule est fausse.
On a souvent tendance à confondre la fonction composée u(x)n avec la fonction xn.
La dérivée de cette fonction composée est égale au produit de la dérivée de u(x) par rapport à x par celle de un par rapport à u.
On devra ainsi remplacer la formule fausse ci-dessus par :
 
 [u(x)n] ' = u ' (x) . n . [u(x)n - 1]
 
Exemple :
 
On donne u(x) = x2 – 1.

On demande de calculer [u(x)3] '.

En appliquant la formule ci-dessus, on trouve :

[u(x)3] ' = [(x2 – 1)3] ' = (x2 – 1) ' . 3 . [(x2 – 1)3 – 1] = 3 . (2x) . (x2 – 1)2 =

6x(x2 – 1)2

 

 

 

 

 

 

f et g deux fonctions numériques quelconques

f o g = g o f


la composition des fonctions numériques n'est pas commutative.

Donc cet énoncé est faux.

Généralement, la fonction composée f o g est différente de la fonction composée
g o f.

Exemple :

Soient les deux fonctions numériques f et g définies comme suit :

f(x) = x2
g(x) = x + 1

On a :

g o f (x) = g [f(x)] = g [x2] = x2 + 1
f o g (x) = f [g(x)] = f [x + 1] = (x + 1)2

Or, les expressions x2 + 1 et (x + 1)2 sont différentes; donc g o f est différente de f o g.



 

 

 

 

 

Une suite numérique est une succession de nombres réels.

Cette définition de la suite numérique manque de rigueur.

La succession de nombres réels n'est qu'une conséquence d'une suite numérique.

Une suite numérique est une application d'une partie A de N, N étant l'ensemble des nombres entiers naturels, dans R, R étant l'ensemble des nombres réels.

La partie A est généralement N ou N* = N - {0}.

Rappel :

Une application d'un ensemble E dans un ensemble F est une relation de E vers F telle que tout élément de E possède par cette relation une image et une seule dans F.

Exemple d'une suite numérique

L'application f de N* dans R définie comme suit :

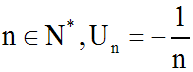
est une suite numérique.

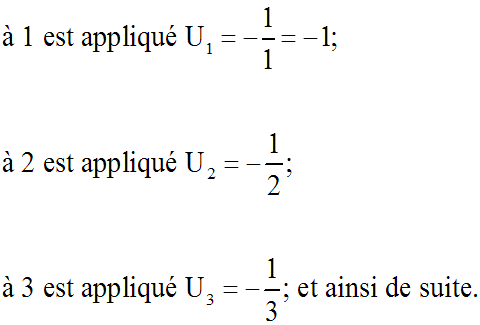
Ainsi, en gardant à l'esprit qu'une suite n'est rien d'autre qu'une fonction de N dans R, on comprend mieux les notions telles que suite convergente ou divergente ( c'est-à-dire son comportement lorsque n tend vers l'infini), suite constante, suite croissante ou décroissante.

Dans notre exemple ci-dessus, la limite de Un lorsque n tend vers l'infini est 0; 0 étant un réel constant fini, Un est donc une suite numérique convergente : elle converge vers 0 lorsque n tend vers l'infini.
 

 

 

 

 

 

 

 

f ' (x0) = 0, donc la courbe représentative (C) de f, fonction continue sur son domaine de définition, admet un extrémum (minimum ou maximum) en x0.

Le fait que la dérivée s'annule en un point x0 appartenant au domaine de définition d'une fonction numérique dérivable n'est pas suffisante pour que sa courbe représentative (C) ait un extrémum au point x0.

Il faut adjoindre à cette condition celle portant sur le signe de cette dérivée : f ' devra s'annuler en changeant de signe.

Ainsi, pour démontrer que (C) admet un extrémum au point x0, il suffit de démontrer que la dérivée s'annule au point x0 en changeant de signe.

D'où la nécessité d'étudier le signe de l'expression de la dérivée dans un voisinage de x0.

 

 

 

 

 

 

f fonction numérique deux fois dérivable sur son domaine de définition.

f '' (x0) = 0; donc la courbe représentative (C) de f admet un point d'inflexion en x0.

Le fait que la dérivée seconde s'annule en un point x0 appartenant au domaine de définition d'une fonction numérique deux fois dérivable n'est pas suffisante pour que sa courbe représentative (C) ait un point d'inflexion en x0.

Il faut adjoindre à cette condition celle portant sur le signe de cette dérivée seconde :
f '' devra s'annuler en changeant de signe.

Ainsi, pour démontrer que (C) admet un point d'inflexion en x0, il suffit de démontrer que la dérivée seconde s'annule au point x0 en changeant de signe.

D'où la nécessité d'étudier le signe de l'expression de la dérivée seconde dans un voisinage de x0.
 

 

retour au sommaire