GESTION DE MATHS FLASH (18)

Le calcul intégral reste l'outil très efficace dans la résolution de problèmes qui relèvent de domaines divers des sciences ou de la technologie

La liste des formules d'intégrales usuelles exposées dans cette page, loin d'être exhaustive, te permet cependant de retenir l'essentiel

 

 

 


Rappel des formules d'intégrales usuelles

 

On suppose dans la suite que toutes les fonctions numériques  utilisées sont intégrables sur leurs domaines de définitions; cependant, pour lever des incertitudes, je préciserai de temps en temps les conditions qui s'imposent à la situation qui se présente.

Dans tout ce qui suit on supposera que toutes les fonctions numériques utilisées sont intégrables sur l'intervalle [ a ; b] et dérivables sur ce même intervalle lorsque leurs dérivées apparaissent dans l'expression sous la somme.

 

 

 

 

 

 

 

 

 

 




 Démonstration

La notation différentielle permet, non seulement d'écrire u ' dx = du, mais aussi d'appliquer les premiers résultats ci-dessus sans ce soucier de la variable indépendante; donc :

uu ' dx = u du et ainsi :

 

 

 

 



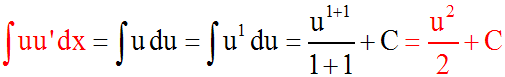
 Je te laisse démontrer cette formule en te basant sur ce qui a été dit plus haut.






 u fonction numérique (non identiquement nulle) définie sur son domaine de définition et ne s'annulant pas sur ce domaine. Alors :


 Démonstration

u ' dx = du et ainsi, on a :

 

 

 

 

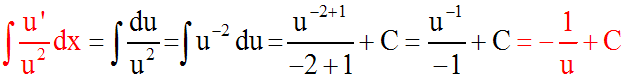
u fonction numérique positive définie sur son domaine de définition. Alors :



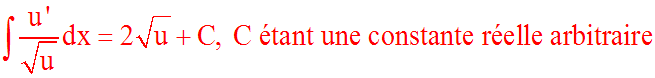
 Démonstration

u ' dx = du et ainsi :

 

 

 

 

 

 

 

 

 

 




 a réel différent de 0



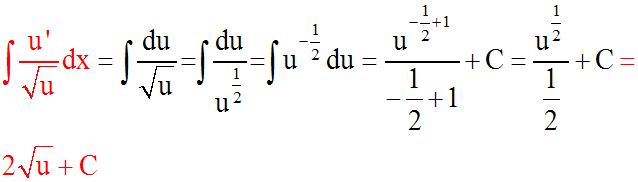
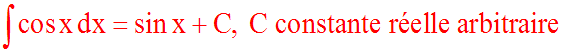
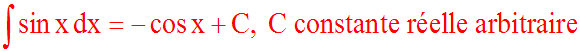
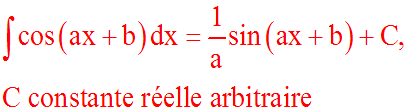
 Démonstration



 

 



 

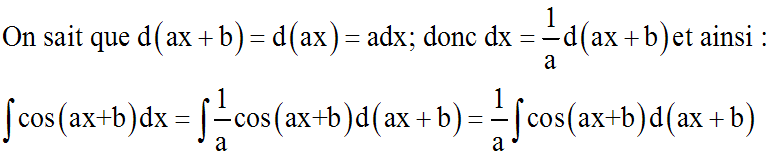
a réel différent de 0



 

 

 

 
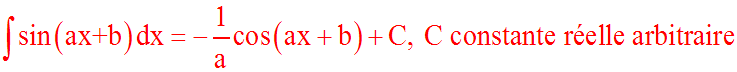
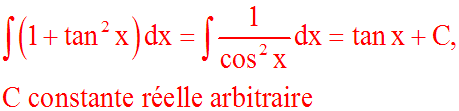
Démonstration


Il est évident que :

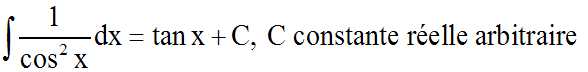
En effet la dérivée par rapport à x, de (tan x + C) est bien :

 

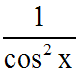
Or, on sait que :

 
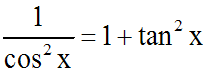
Donc finalement :



 

 

 

 

 

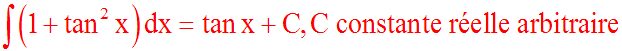
On démontre de la même manière que :

 
 

 

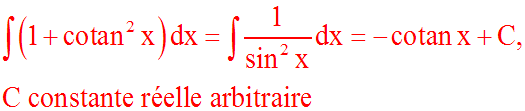
x réel différent de 0



 



 



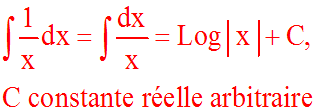
 u fonction numérique définie et dérivable sur son domaine de définition



 

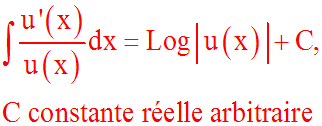
Pour démontrer cette formule, il suffit de remarquer que
u ' dx = du et ainsi :

 



 



 

 

 

 

 

 

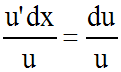
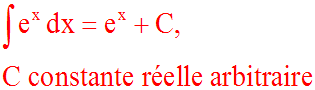
u fonction numérique





 

 

 

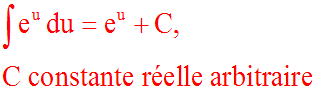
a réel différent de 0
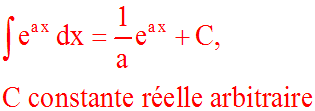
Démonstration

On sait que :

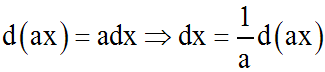
En remplaçant cette valeur de dx dans la somme, on obtient :



 

 

 

 

 

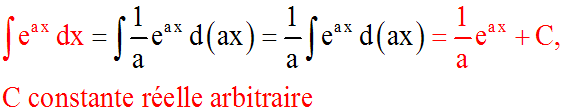
a réel strictement positif et différent de 1



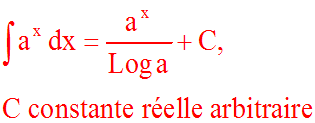
 Démonstration

Posons u(x) = a x.

On a :

Log u(x) = x Log a implique u(x) = e x Loga

Ce qui se traduit aussi par :

 

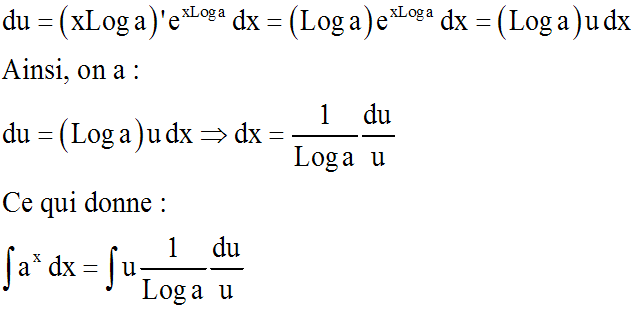
Comme u est différent de 0 et comme a appartient à (R*+) – { 1 }, on peut alors simplifier par u dans le second membre; ce qui donne :


 

 

 

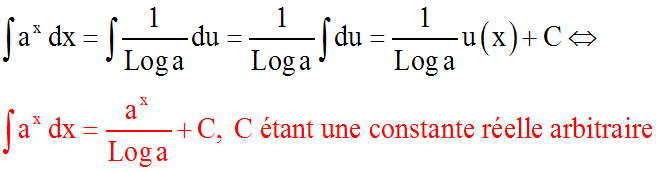
u fonction numérique dérivable sur son domaine de définition
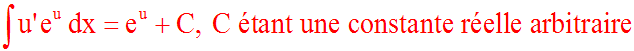
Cette formule est évidente puisque la dérivée de e u est u ' e u.




 

 

a réel différent de - 1

La fonction (xa) étant définie sur R*+
 


 

Je te laisse démontrer cette formule.

 

Remarques sur cette fonction

1- Cette fonction, définie sur R*+ s'appelle fonction puissance.

2- Elle est logiquement équivalente à la fonction :

f(x) = e a . Log x

Donc les propriétés et l'étude de l'une découlent de celles de l'autre.

En particulier :

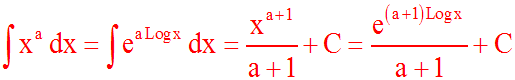
C étant une constante réelle arbitraire

 

 

 

 

Remarque importante

L'utilisation de la différentielle en ne souciant plus de la variable indépendante
(c'est-à-dire en écrivant du , u étant la variable indépendante ou non ), est un moyen sûr pour éviter les erreurs.

 

 

retour au sommaire