Application des équations différentielles à la Géométrie et à la Physique - Deuxième partie
Un corps de masse m tombe d'une certaine hauteur, avec une vitesse initiale v0 à l'instant t = 0.
On nous demande d'établir la loi de variation de la vitesse de sa chute, v, s'il éprouve en tombant une résistance de freinage de la part de l'air, proportionnelle à la vitesse de chute.
Le coefficient de proportionnalité est donné et est égal à k.
On demande ensuite d'étudier les deux cas particuliers suivants :
v0 = 0
Résistance à l'air nulle
La seconde loi de Newton permet d'écrire :

D'après les données du problème, F est composée de deux forces :
- la force de pesanteur mg
- la résistance de l'air - kv ( on a pris cette
valeur négative car cette force est opposée à la vitesse)
Ainsi, on peut écrire :
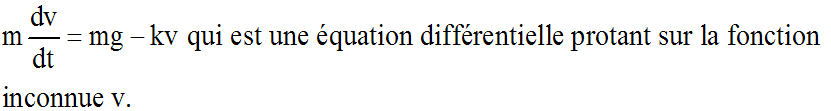
Elle est de la forme :
a y ' + b y + c = 0, avec y = v, a = m, b = k et c = - mg.
La résolution de ce type d'équation a été abordée à la
page (billet) intitulée :" Résolution des équations différentielles ( 2ème
partie ) ".
Je te laisse donc poursuivre la résolution de ce problème.
Tu dois trouver les réponses suivantes :
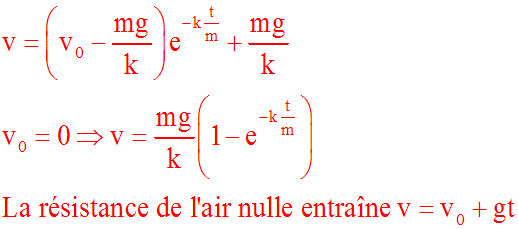
Désintégration du radium
Le radium se désintègre à une vitesse directement proportionnelle
à sa masse à l'instant considéré.
On demande de déterminer la loi de variation de la masse du radium en
fonction du temps, sachant qu'à l'instant t = 0 sa masse était m0.
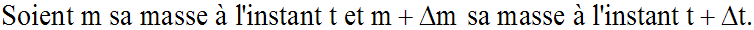

Elle est égale à :
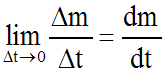
D' après les données et conditions du problème, on écrit :
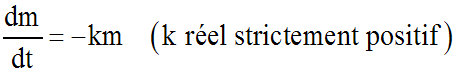
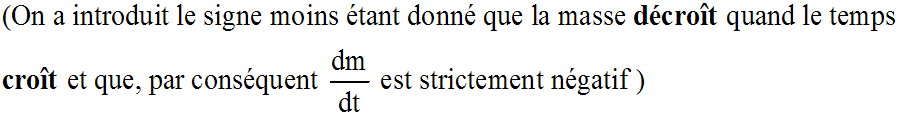
On obtient ainsi une équation différentielle de la forme :
y' + ay = 0, avec y = m, a = k.
La résolution de ce type d'équation a été abordée à la
page (billet) intitulée :" Résolution des équations différentielles ( 1ère
partie ) ".
Je te laisse donc poursuivre la résolution de ce problème.
Tu dois trouver la réponse suivante :
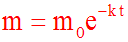
Le pendule mathématique
Un point matériel de masse m se meut sous l'action de son poids sur une
circonférence (C) située dans un plan vertical.
On demande de trouver l'équation de son mouvement.
Toutes les forces de résistance, telles que la résistance
de l'air, les frottements, sont supposées négligeables.
Soit O l'origine d'un repère orthonormal confondu avec le point le
plus bas de (C). L'axe des abscisses Ox est pris tangentiellement à
(C) au point O. L'axe des ordonnées Oy a le sens dirigé vers le haut.
Soit r le rayon de (C) et s la mesure géométrique de la portion d'arc de
cercle de l'origine O au point M variable de masse m. ( s > 0 si M est à
droite de O, sinon s < 0 )
On se propose de trouver la relation liant s au temps t.

L'équation du mouvement s'écrit alors :
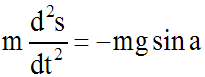
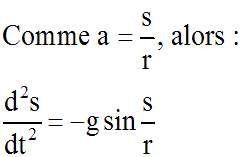
On obtient ainsi l'équation différentielle
recherchée.
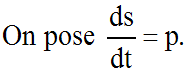
On a donc
:

Par conséquent,
on obtient :
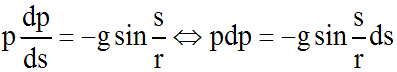
En intégrant :
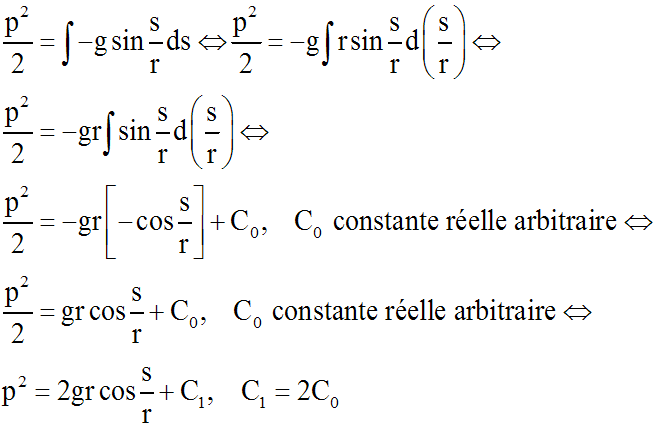
Si s0 est l'élongation
maximale de M,
alors sa vitesse est nulle lorsque s = s0
.
On a donc :
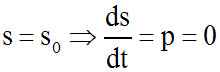
On obtient :
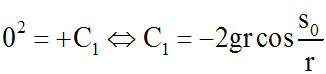
Par conséquent,
on peut écrire :
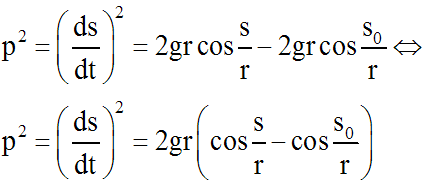
On sait que (relation trigonométrique) :
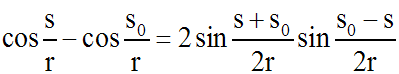
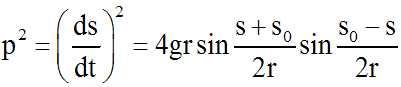
On obtient une équation à variables séparables. En séparant ces dernières, et en supposant (s - s0) différent de 0, donc s différent de s0, on obtient :
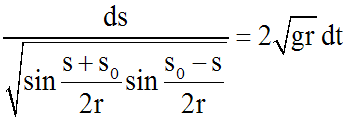
En supposant s = 0 pour t = 0, on obtient :
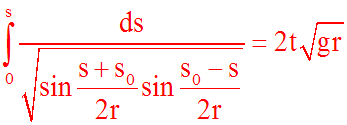
On obtient ainsi la relation liant s à t.


En séparant les variables, il vient :

Comme s = 0 pour t = 0 et en intégrant, on obtient :
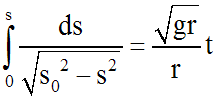

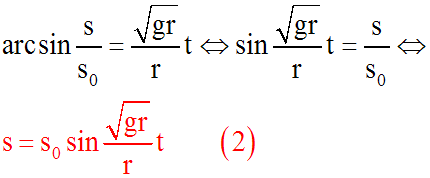
Remarques :
1- On a supposé que s était différent de s0 ; cependant on peut facilement
vérifier que la fonction s (t) obtenue ci-dessus est solution de notre équation
différentielle (1), ceci pour tout t.
2- La relation (2) ci-dessus montre que le point M accomplit des
oscillations harmoniques de période :
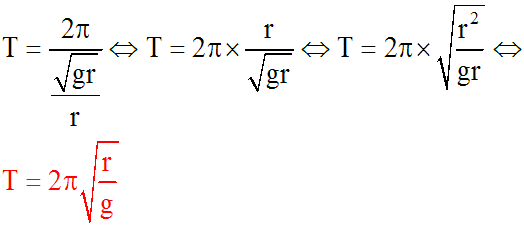
A quelle vitesse faut-il lancer un corps vers le haut et verticalement pour qu'il échappe à l'attraction terrestre?
Si M est la masse de la Terre et m celle du corps, on admettra que ce corps est sollicité par une force f telle que son module f est égal à :
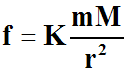
r est la distance séparant le centre de la Terre du centre
de gravité du corps.
K est la constante de gravitation universelle.
C'est la loi d'attraction de Newton.
On sait que l'équation
différentielle du mouvement de ce corps est :
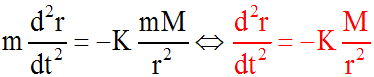
On a pris ici - K car l'accélération est négative.
On définit d'abord les conditions initiales suivantes :
t = 0 implique r = R, R étant le rayon
de la Terre supposé constant et

Soient les notations :
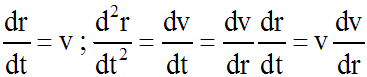
L'équation s'écrit donc :
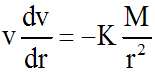
En séparant les variables :
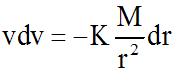
En intégrant :
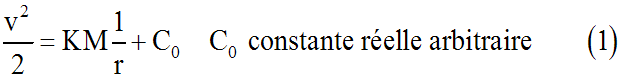
A la surface
de la Terre, v = v0 et r = R; ceci permet de calculer C0 :
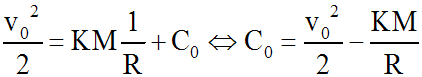
La relation (1) devient :
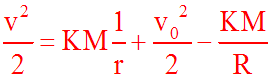
La vitesse du corps devra rester
constamment strictement positive : elle ne s'annule pas.
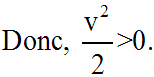

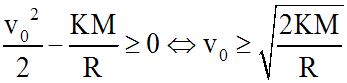
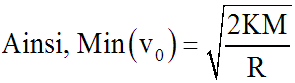
Sur la surface de la Terre, r = R et l'accélération est égale à g; donc :
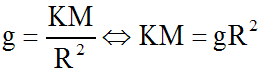
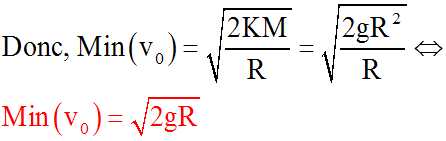
Application numérique :
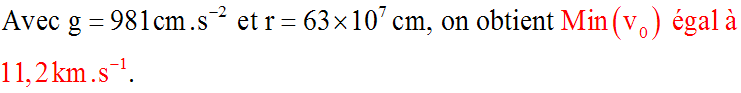
Electricité
Un circuit électrique, muni d'une résistance R ( exprimée en ohms ), est parcouru par une intensité de courant j ( t ), t étant le temps exprimé en secondes (s) et j étant exprimée en Ampères (A).
On demande :
1- de démontrer que ce courant électrique est alternatif, de période T que l'on calculera, sachant que :
j '' + 4 j = 0
et
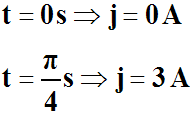
Ce sont là ce qu'on nomme " conditions initiales
" en Physique.
2- de calculer la quantité d'électricité q, exprimée en
coulombs (c), traversée dans le circuit durant une alternance (c'est-à-dire durant la moitié d'une période)
3- de calculer la puissance P fournie au système, exprimée en
watts (W)
4- de calculer l'énergie calorifique, exprimée en Joules
(J), dissipée dans le circuit pendant une période, sachant
qu'elle est entièrement dépensée par la résistance R, et d'en
déduire l'intensité efficace Je
1-
La relation j '' + 4 j = 0 est une équation différentielle de
la forme :
y '' + a y ' + b y = 0, avec a = 0, b = 4.
Son équation caractéristique est :
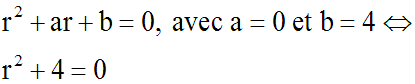
Le discriminant de cette équation caractéristique est :
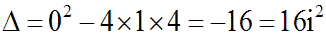
Ses racines sont donc les deux nombres complexes
conjugués r1 et r2 :
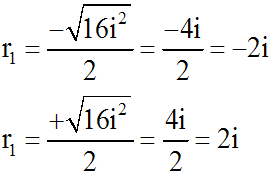
On a démontré, à la page ( billet ) intitulée " Résolution des équations
différentielles
(1ère partie) ", que la solution générale de l'équation
différentielle donnée est :
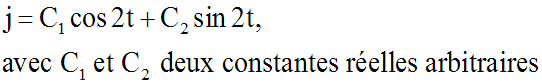
Les conditions initiales donnent :
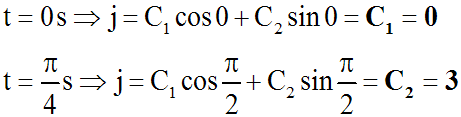
La solution de notre équation différentielle est donc :
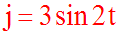
A = 3; sa période est par définition :
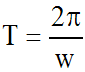
Donc, sa période est :
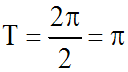

2-
Par définition :
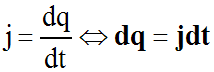
C'est une équation différentielle et, dans notre cas, on peut s'écrire :
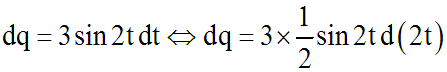
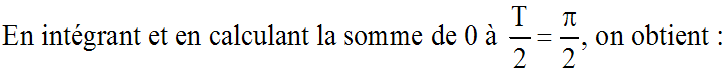
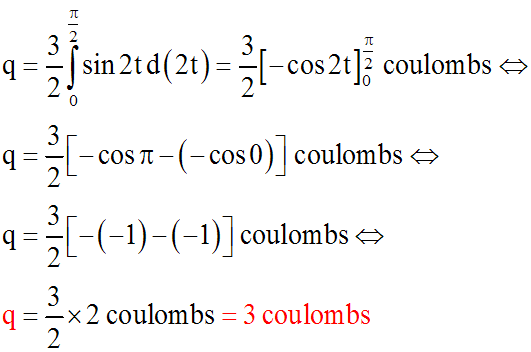
3-
Par définition :
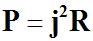
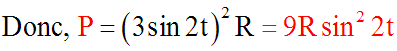
4-
Par définition :
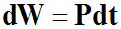
C'est une équation différentielle qui, dans notre cas, elle peut s'écrire :

On sait que (relation trigonométrique) :
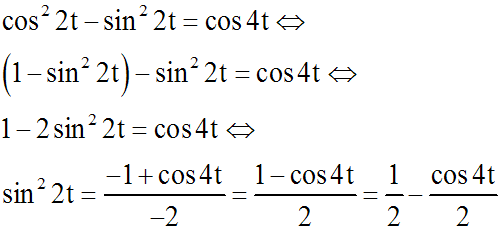
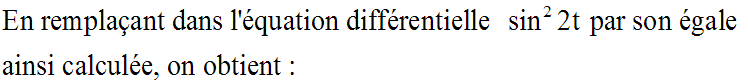
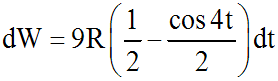
En intégrant et en calculant la
somme de 0 à T, on obtient :
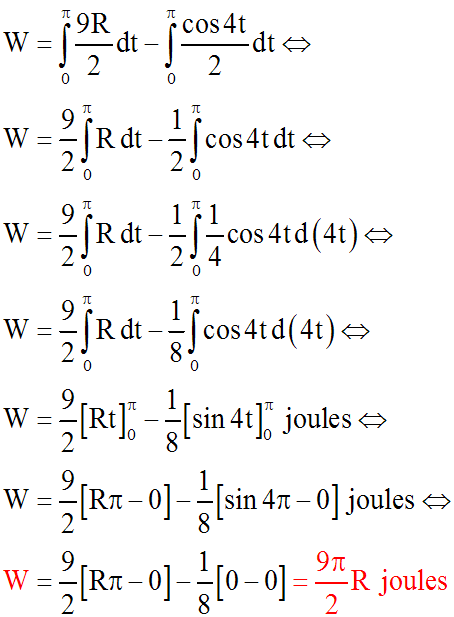
Par définition, l'intensité
efficace Je est celle d'un courant
continu qui, pendant la même
période T, fera dissiper la même énergie W.
On a donc :