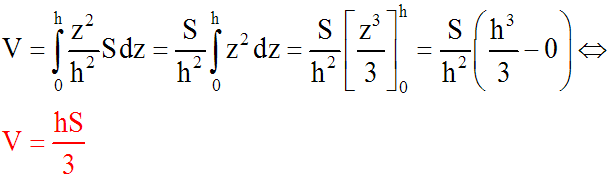La Géométrie et la Physique ont
souvent recours à l'équation différentielle permettant de résoudre des
situations concrètes. Cependant, il faut savoir que , pour les sciences
physiques, cela n'est possible que si ces situations peuvent être approchées
par des modèles mathématiques linéaires.
Cette page abordera les différents cas d'applications sans prétendre être exhaustif.
Cette page abordera les différents cas d'applications sans prétendre être exhaustif.
1- Application à la Géométrie
Aires de l'ellipse et du cercle
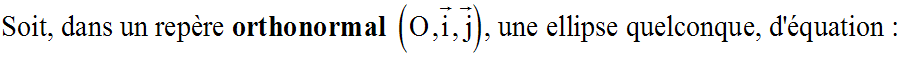
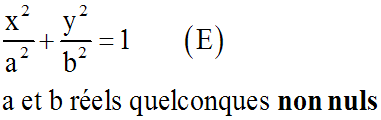
Soit M (x ; y) un point quelconque du premier quart de (E).
La parallèle menée de M à l'axe des ordonnées coupe l'axe des abscisses au point m(x).
Au point m' (x + dx) menons une parallèle à l'axe des ordonnées qui coupe (E) au point M'.
Soit dS l'élément de surface de (Mmm'M').

On obtient donc l'équation différentielle :
dS = y . dx
En intégrant les deux membres, on obtient l'aire du premier quart de (E) :

A partir de l'équation de (E), et comme a et b sont différents de 0, on peut obtenir y :
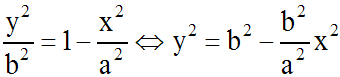
Comme sur le premier quart de (E) les ordonnées sont largement positives, on obtient alors :
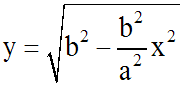
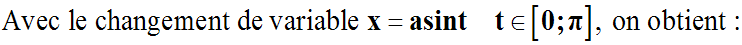
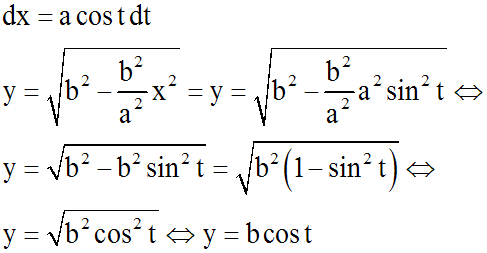
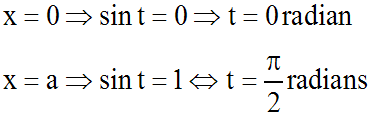
L'équation différentielle s'écrit
alors :
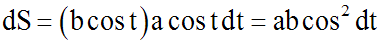
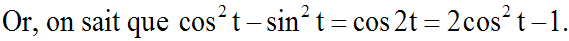
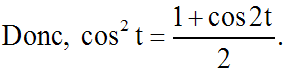
Ainsi :
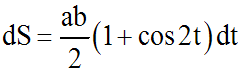
On a donc :
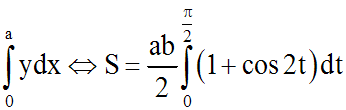
Ce qui donne en calculant l'intégrale :
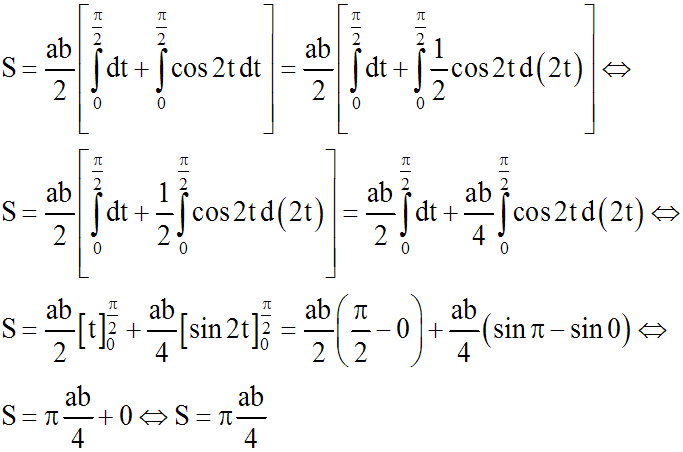
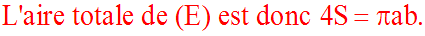
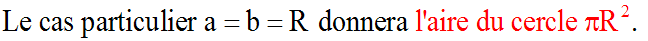
Aire du triangle
On nous demande d'établir la formule
permettant de calculer l'aire d'un triangle.
Soit (ABC) un triangle quelconque et [HB] la hauteur relative au côté [AC], H étant le pied de cette hauteur sur [AC].
Posons HB = h et AC = b.
Soit (ABC) un triangle quelconque et [HB] la hauteur relative au côté [AC], H étant le pied de cette hauteur sur [AC].
Posons HB = h et AC = b.
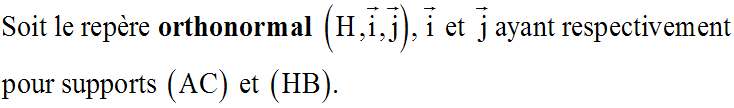
Soit M ( y ; 0 ) un point quelconque de [HB].
Soit M' ( y + dy ; 0 ) un point de [HB] différent de M.
Menons de M et de M' les parallèles respectives (d) et (d') à (AC). (d) coupe (BA) et (BC) respectivement aux points N et P; (d') coupe (BA) et (BC) respectivement aux points Q et R.
L'élément d'aire de (NQRP), noté dS, vaut donc :
dS = NP . dy
On obtient ainsi une équation différentielle.
Or, d'après le théorème de Thalès, on a :
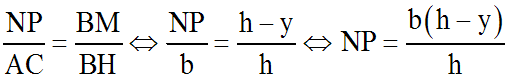
L'équation différentielle ci-dessus s'écrit alors :
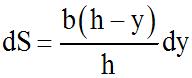
En intégrant les deux membres, on obtient :
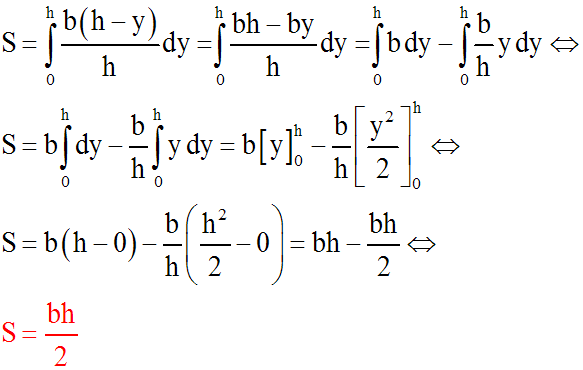
Volumes de solides
Volume de la sphère
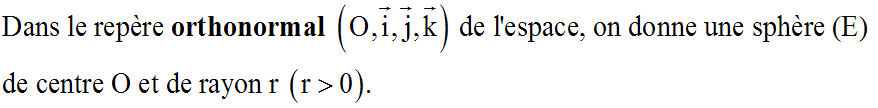
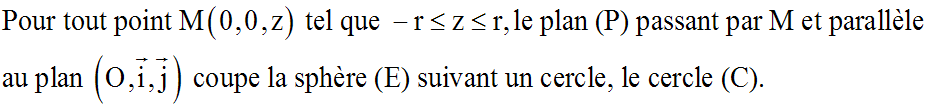
Soit A(z) l'aire de ce cercle (C) et [MN] un rayon quelconque.
D'après le théorème de Pythagore appliqué au triangle (OMN), rectangle en M, on a :
D'après le théorème de Pythagore appliqué au triangle (OMN), rectangle en M, on a :
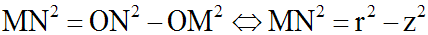
Ainsi, on a :
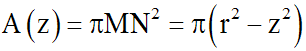
Soit M' ( z + dz).
On obtient l'élément de volume :
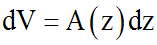
En intégrant les deux membres, on obtient :
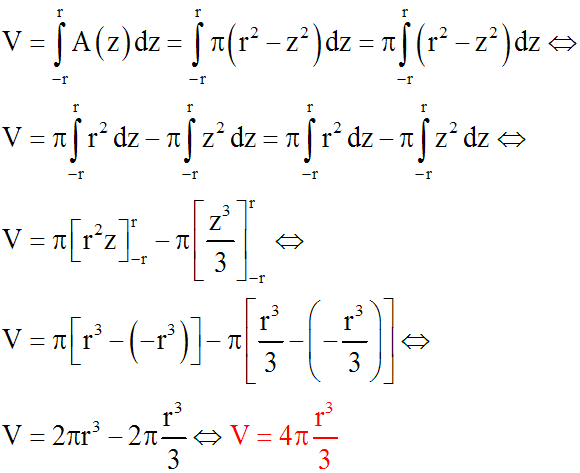
Volume d'une pyramide
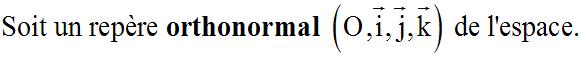

On pose OH = h et S l'aire de sa base (ABC).
On se propose de calculer son volume V.
Soit un plan (Q) parallèle à sa base qui coupe la pyramide selon la section
triangulaire
(A' B' C') et soit H' l'intersection de [OH] et de (A' B' C'). On pose OH'
égale à z et S' l'aire de (A'B'C').
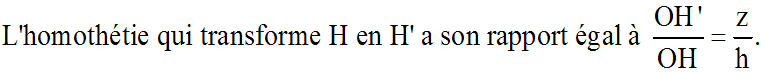

On obtient :
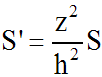
Soit le point H'' (0 ; 0 ; z + dz).
On obtient ainsi l'élément de volume :
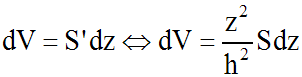
En intégrant les deux membres de cette équation différentielle dans l'intervalle [0 ; h], on
obtient le volume V de cette pyramide
égal à :