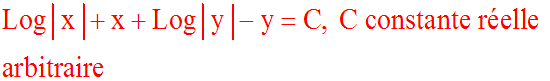L'équation peut s'écrire :
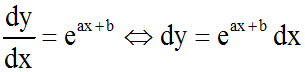
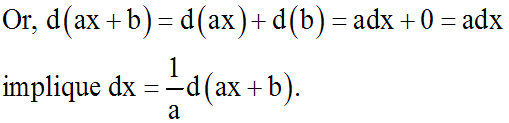
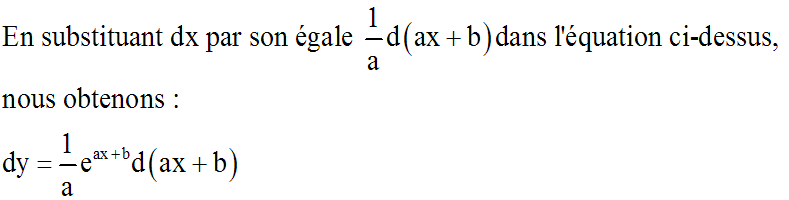
En intégrant les deux membres :
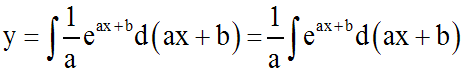
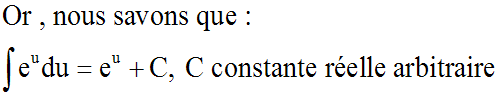
Donc finalement :

Résolution des équations différentielles de la forme ay ' + by + c = 0, avec a, b constantes réelles non nulles quelconques et c constante réelle quelconque
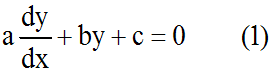
a étant différent de 0, on peut diviser les deux membres de
l'équation par a; on obtient :
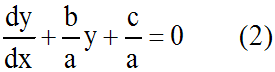
On cherchera les solutions de cette équation de la forme :
y = u(x) . v(x) où u(x) et v(x) sont deux fonctions numériques
dérivables (3)
Dérivons les deux membres de l'égalité (3), on trouve :
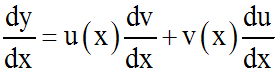
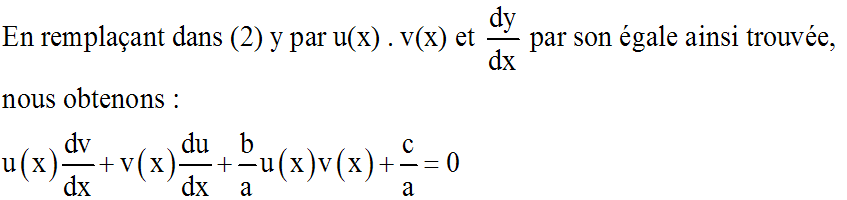
Cette dernière équation peut s'écrire :
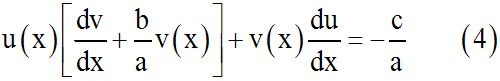
Nous allons choisir la fonction v(x) de telle sorte que :

En séparant les variables dans cette dernière égalité, nous obtenons :
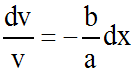
En intégrant les deux
membres, nous obtenons :
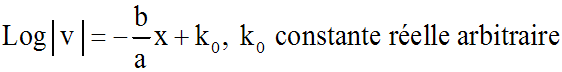

Comme il nous suffit de prendre une solution quelconque non nulle
pour (5), nous prendrons :
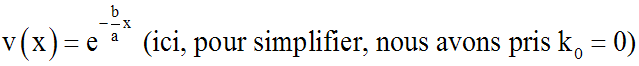
Substituons cette valeur trouvée de v(x) dans (4), en tenant compte de
la nullité de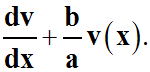
Nous obtenons :
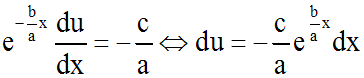
En intégrant, nous obtenons :
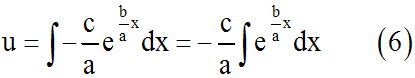
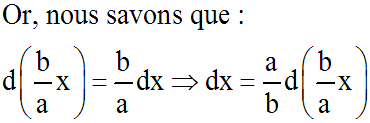
Ainsi, en remplaçant, dans (6), dx par son égale ci-dessus,
nous obtenons :
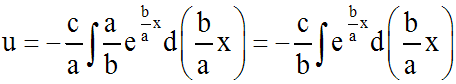
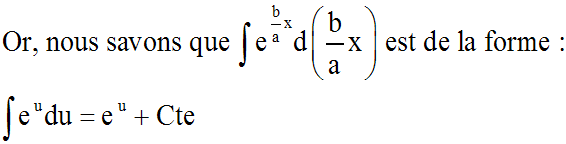
Donc finalement :
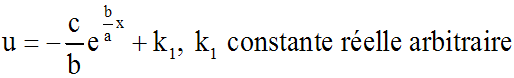
La solution générale de l'équation donnée est
donc :
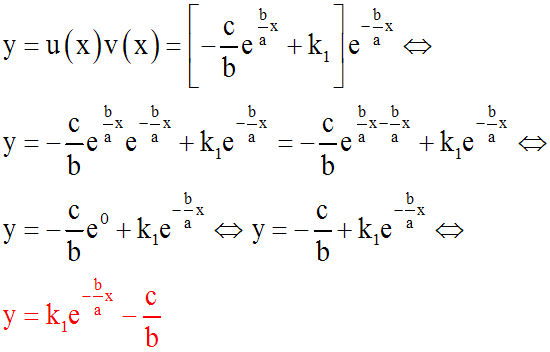
Résolution des équations différentielles à variables
séparées
Soit l'équation différentielle de la
forme :
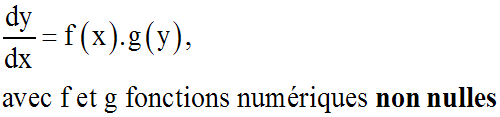
On peut donc écrire :

En intégrant chaque membre, on obtient :
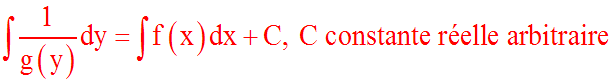
L'équation différentielle de la forme :
M(x) dx + N(y) dy =
0, avec M, N non nulles,
est appelée équation différentielle à variables
séparées.
Sa solution générale est :
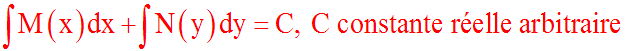
Exemple :
Résous l'équation
x dx + y dy = 0
C'est une équation à variables séparées. On a donc :
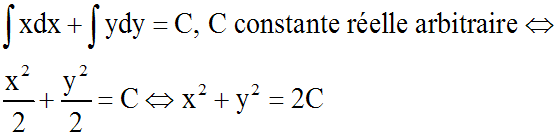
Le premier membre n'étant pas négatif, il en est de même du second; donc 2C est
largement positif.
En posant 2C = K, on obtient finalement :
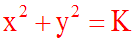
C'est l'équation d'une famille de cercles tous centrés à l'origine du repère, et
de rayon r égal à :
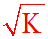
Résolution d'une équation différentielle à variables séparables
Une équation de la forme :
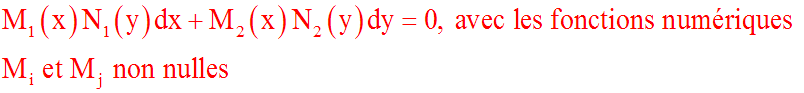
est appelée équation différentielle à variables
séparables; c'est-à-dire qu'elle peut être ramenée à une
équation à variables séparées, en divisant les deux membres par

On obtient ainsi :
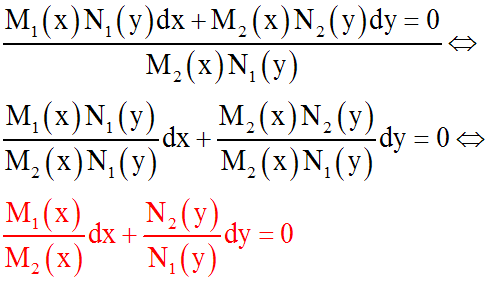
Ainsi, cette dernière équation
est à variables séparées
dont la résolution a été abordée précédemment.
Exemple :
Résous l'équation :
( 1 + x ) y dx + ( 1 - y ) x dy = 0
Séparons les variables :
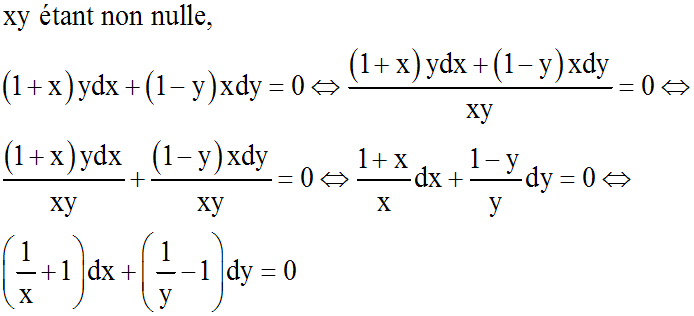
En intégrant :