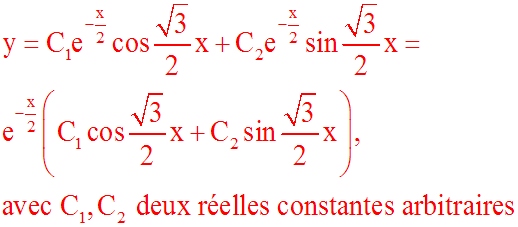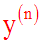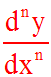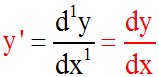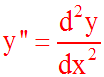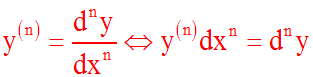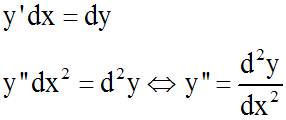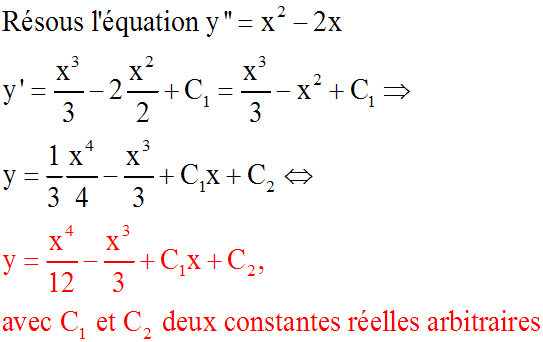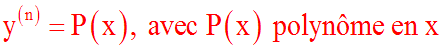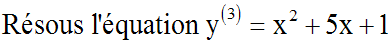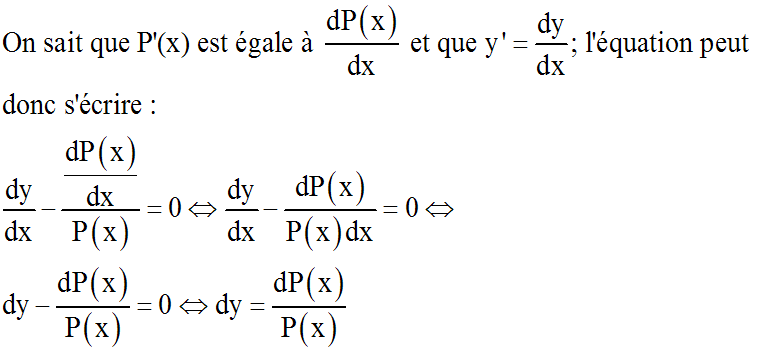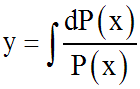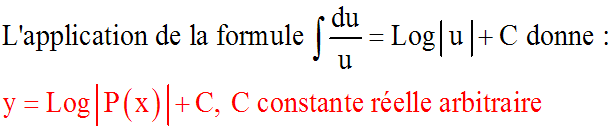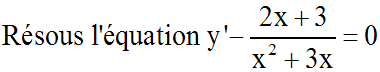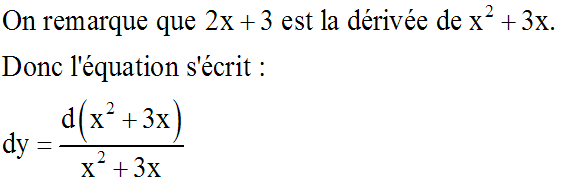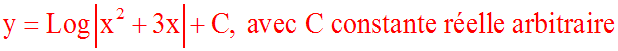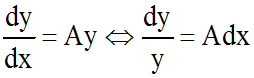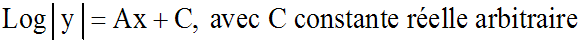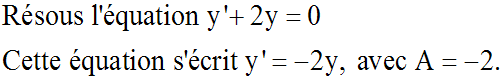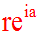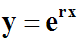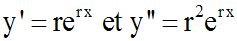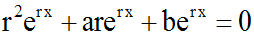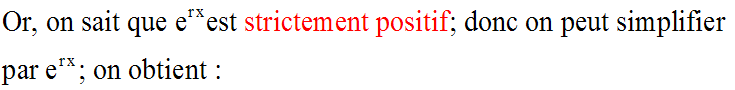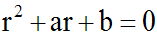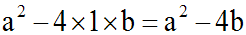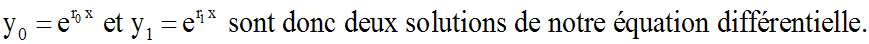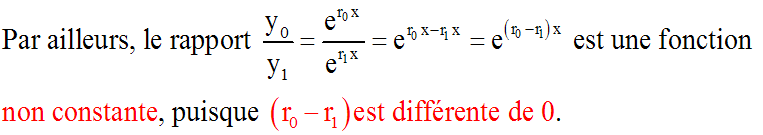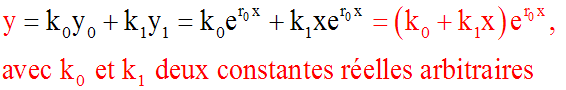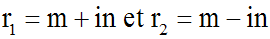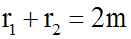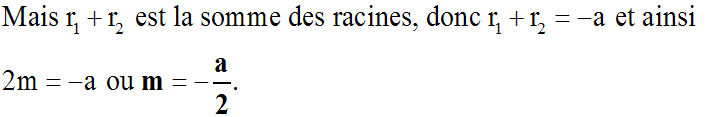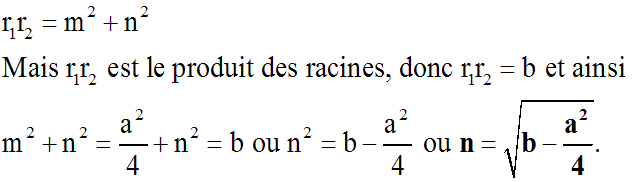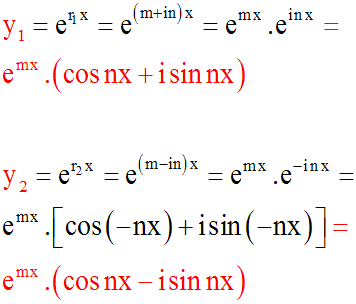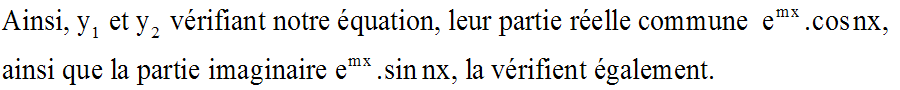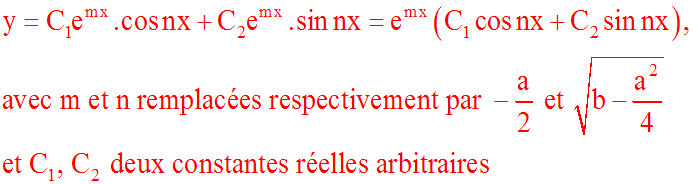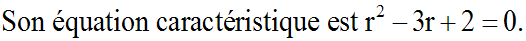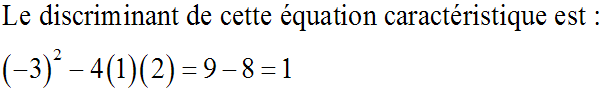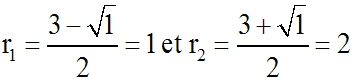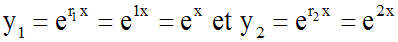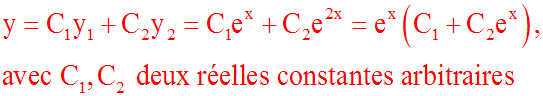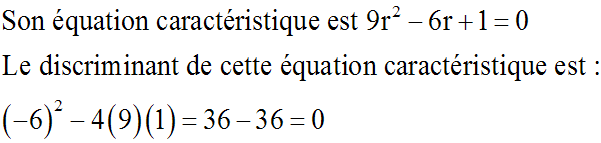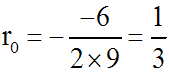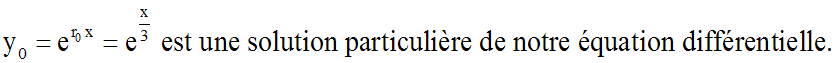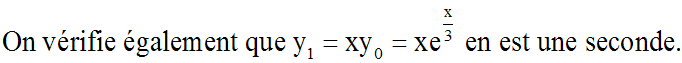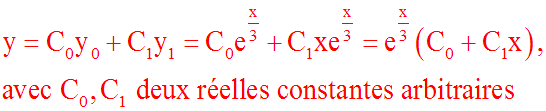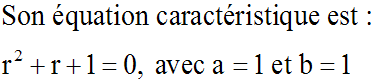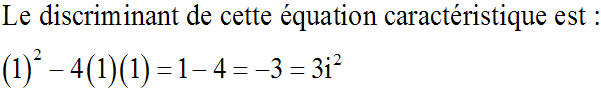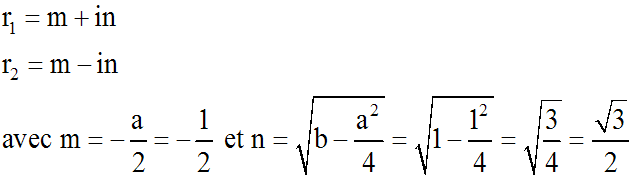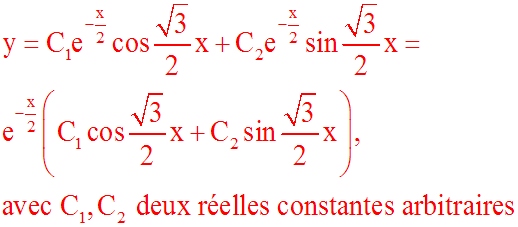Une équation
différentielle est une relation dans laquelle les fonctions
dérivées d'ordres quelconques sont liées à la fonction initiale, ainsi
qu'à la variable indépendante.
Exemples :
2y' + 3x = 0 est une équation différentielle.
Dans cette équation, la dérivée première ou d'ordre 1, y', est liée à la
fonction initiale y (ici 0 . y = 0) et à la variable indépendante x.
-5y'' + 4y' - 5y = x est une équation
différentielle. Dans cette équation, la dérivée seconde ou d'ordre 2, y'', et la
dérivée première ou d'ordre 1, y', sont liées à la fonction y et à la variable
indépendante x.
3y'' + y' - 4y = 0 est une équation
différentielle dans laquelle les dérivées seconde y'' et première y' sont liées
à la fonction initiale y.
L'ordre
d'une équation différentielle est celui de la dérivée qui a
le plus grand ordre.
Ainsi, dans les exemples ci-dessus, la première équation est dite du 1er ordre;
quant aux deux dernières, elles sont du 2ème ordre.
Résoudre
une équation différentielle consiste à trouver
toutes les fonctions qui la vérifient.
Exemple :
y' = 2, a pour solutions toutes les fonctions de la forme
y = 2x + C, avec
C constante réelle arbitraire.
Une solution particulière est y = 2x (on a posé C = 0)
Dans
cette page, on abordera la résolution des équations différentielles inscrites
dans le programme de la terminale S
Notation
Une dérivée d'ordre n quelconque
qui s'écrit :
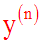
s'écrit également
:
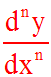
Exemples :
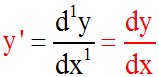
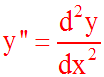
Ainsi, on a
:
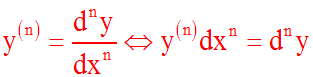
Exemples :
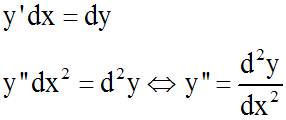
On a les propriétés importantes suivantes
:

Equation de la forme y''+ P(x) = 0 avec P(x) un polynôme en x de degré
quelconque
On a donc y'' = - P(x) et par un
premier passage à la somme, on obtient :
y' = Q(x) + C1 avec Q(x) une primitive
quelconque de P(x) et C1
une constante réelle arbitraire.
A partir de cette dernière équation et par un second passage à la somme, on
obtient :
y = R(x) + C1x
+ C2
avec R(x) une primitive quelconque de Q(x) et
C1,
C2 des constantes
réelles arbitraires.
Exemple :
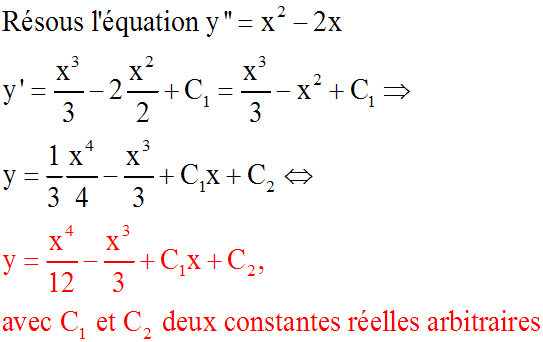
Généralisation
Par
une succession de passages à la somme, on pourra résoudre une
équation de la forme :
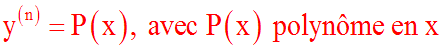
et ainsi,
remonter jusqu'à la solution.
Exemple :
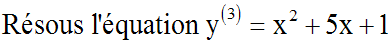
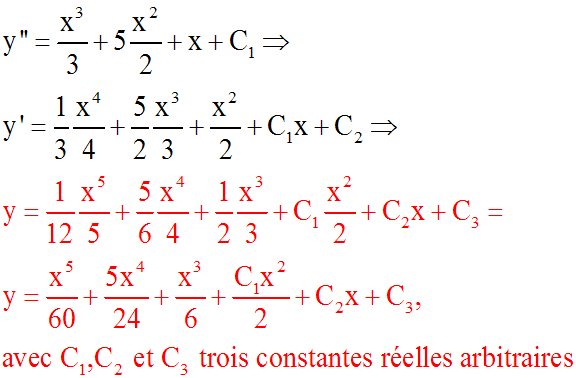

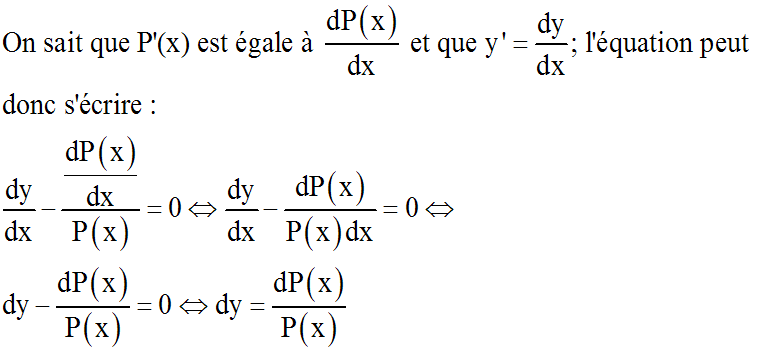
Le passage à la somme
donne :
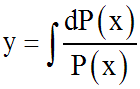
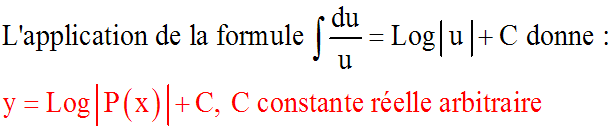
Exemple
:
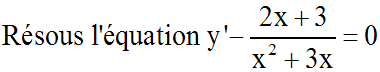
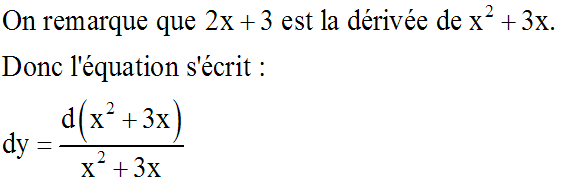
Par passage à la somme, on obtient :
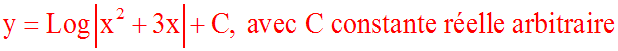
Equation de la forme y' = Ay, avec A constante réelle différente de 0
Cette équation peut également s'écrire :
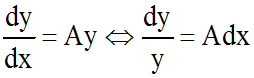
Le passage à la somme donne :
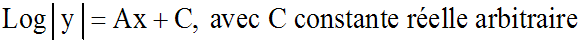

Exemple :
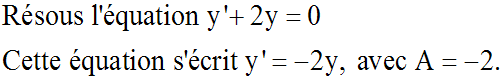
En appliquant le résultat général ci-dessus, on obtient :

Equation de la forme y'' +
ay' + by = 0, avec a, b deux constantes réelles, différentes de zéro,
quelconques
Remarques et définitions préalables
1-
Toute équation de la forme y'' + ay' + by = 0, avec a, b constantes réelles
quelconques, est dite
équation linéaire du second ordre. Elle est linéaire du fait qu'elle soit
du premier degré par rapport à y, y', y''.
2-
Tout nombre complexe z = r(cosa + isina) peut également s'écrire
:
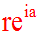
C'est la notation
exponentielle d'un nombre complexe.
3-
L'ensemble E des fonctions réelles d'une variable réelle est un espace vectoriel
sur R.
Dans cet espace, deux fonctions f1 et f2
toutes deux différentes de la fonction nulle 0, sont dites
linéairement indépendantes, si et
seulement si leur rapport est une fonction non
constante.
Exemple :

Résolution de l'équation
L'ensemble des solutions d'une
équation différentielle linéaire du second ordre est un
sous-espace vectoriel de E, de dimension 2.
Dans ce sous-espace, deux fonctions f1 et f2
toutes deux différentes de la fonction nulle 0, sont dites
linéairement indépendantes, si et
seulement si leur rapport est une fonction
non constante.
Nous allons trouver toutes les
solutions de la forme :
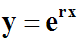
Partant de cette forme, on a successivement :
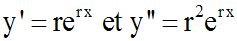
Remplaçons dans l'équation différentielle y, y' et y'' par leurs valeurs
respectives, on obtient :
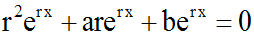
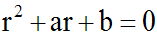
Cette équation
est par définition appelée équation
caractéristique de l'équation différentielle donnée. c'est une
équation du second degré en r.
La résolution de l'équation caractéristique va donc
permettre de calculer les solutions de notre équation différentielle.
Le
discriminant D de notre équation du second degré
est égal à :
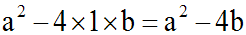
Trois cas sont à envisager : D > 0,
D = 0 et
D < 0
1er cas : D > 0
L'équation caractéristique admet deux
racines réelles distinctes r0 et r1.
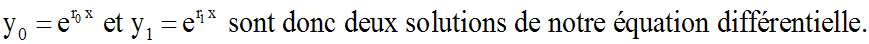
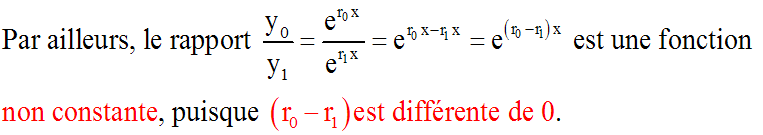
Donc dans le sous-espace vectoriel
des solutions de notre équation,
y0 et y1 sont linéairement indépendantes; une
base est {y0
; y1} et la solution générale de notre équation différentielle est,
dans ce cas, de la forme :

2ème cas : D = 0
L'équation caractéristique admet une racine réelle
double
r0.

Donc,
y0 et
y1 sont deux solutions linéairement indépendantes; {y0
,
y1}
étant ainsi une base dans le sous-espace vectoriel des solutions de notre
équation, la solution générale de notre équation sera :
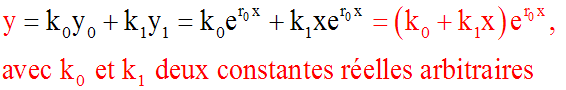
3ème cas : D < 0
L'équation caractéristique
n'admet aucune racine réelle.
Par contre, elle admet deux solutions complexes
distinctes et conjuguées :
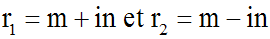
On a :
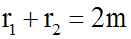
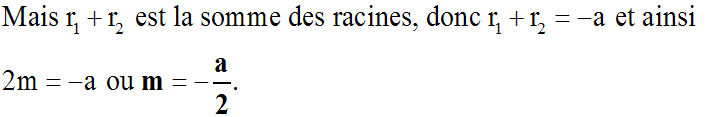
De même, on a :
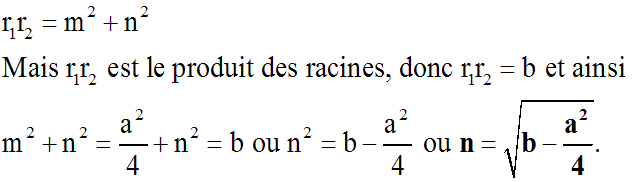
On peut mettre les solutions particulières sous la forme :
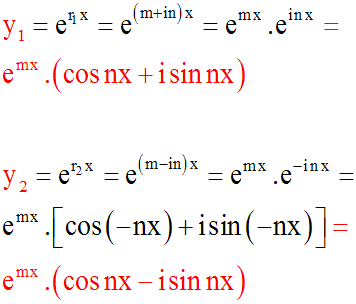
Ce sont là deux fonctions complexes d'une
variable
réelle vérifiant donc l'équation différentielle donnée.
On admettra
que si une fonction complexe vérifie notre
équation différentielle, alors ses parties réelle et imaginaire la vérifient
également.
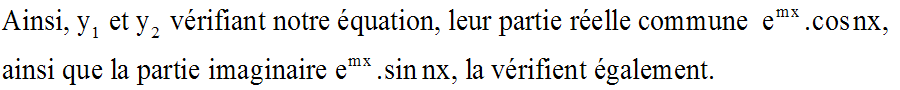
Par ailleurs, ces deux parties, réelle et imaginaire, sont des fonctions réelles
de la variable réelle x; de plus elles ont leur rapport égal à (cotan nx), donc
non constant.
Elles sont ainsi linéairement indépendantes et la
solution générale de notre équation différentielle
sera de la forme :
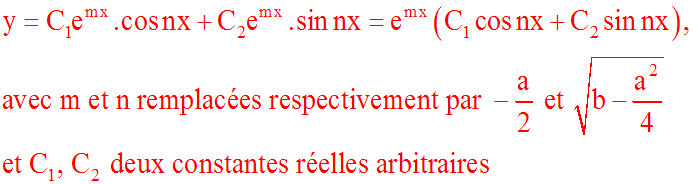
Exemples
1-
Résous l'équation y'' - 3y' + 2y = 0
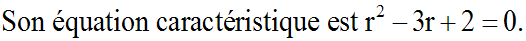
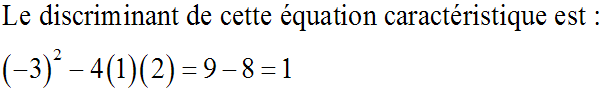
Ce discriminant étant strictement positif,
l'équation caractéristique admet deux racines réelles distinctes :
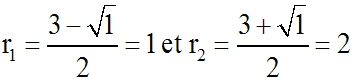
Notre équation différentielle
donnée admet donc les deux solutions réelles particulières :
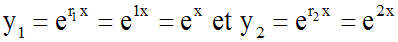

La solution générale de notre équation
différentielle est :
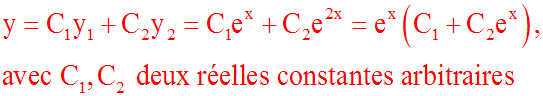
2-
Résous l'équation différentielle :
9y'' - 6y' +y = 0
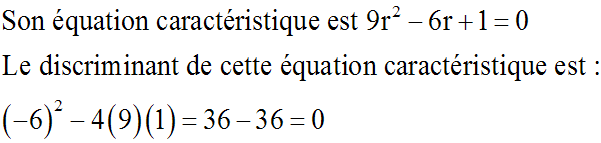
Ce discriminant étant nul,
l'équation caractéristique admet une racine réelle double :
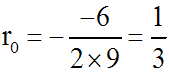
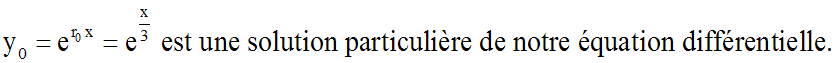
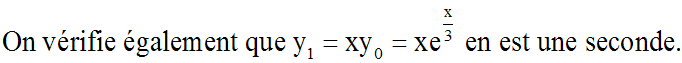

La solution générale de notre équation différentielle
donnée est donc :
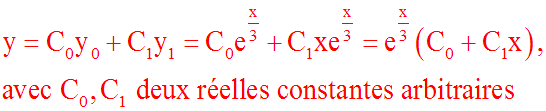
3-
Résous l'équation différentielle :
y'' + y'+ y = 0
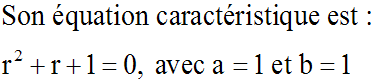
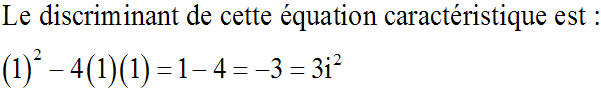
Ce discriminant étant
négatif, l'équation
caractéristique admet deux racines complexes et conjuguées
:
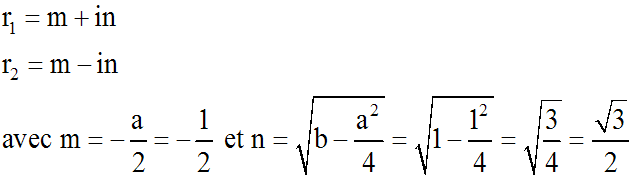
En appliquant les résultats du troisième cas ci-dessus (D < 0), on
obtient la solution générale de notre équation différentielle :