GESTION DE MATHS FLASH

1- Longueur d’un arc de courbe

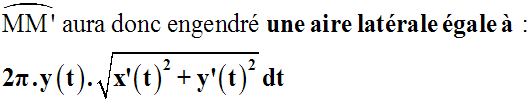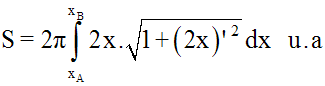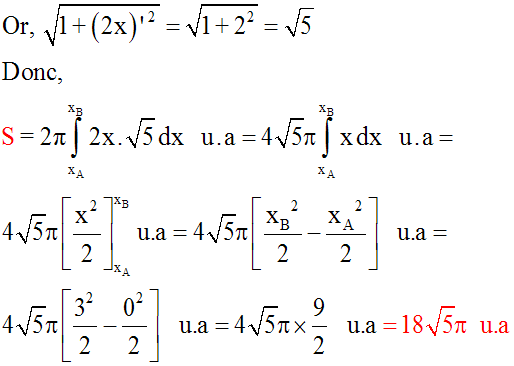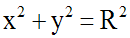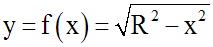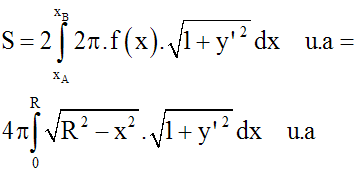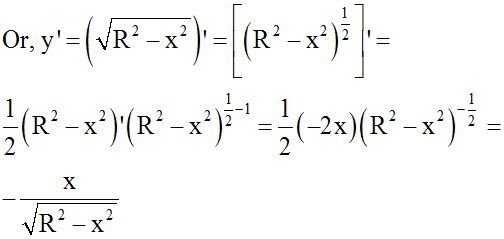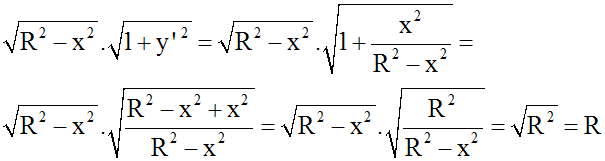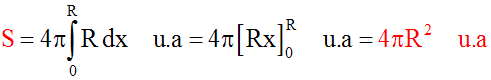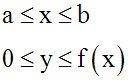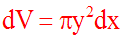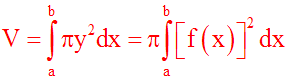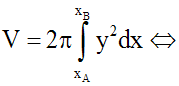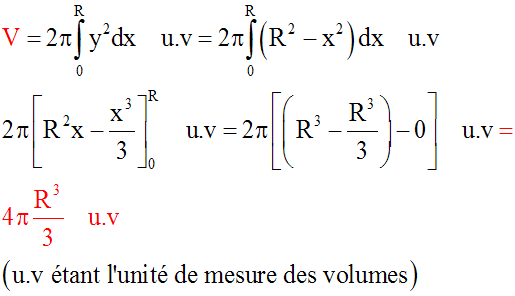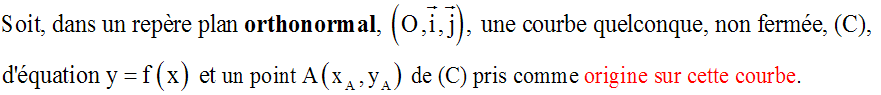
Soit M un point mobile de (C), d’abscisse x et d’ordonnée y. Menons de M la tangente [Mt) à (C) orientée dans le sens de déplacement et la normale [Mn) à (C) dirigée vers son centre de courbure.

On dira que le sens de déplacement sur (C) est positif si l’angle orienté {[Mn) , [Mt)} est positif ( sens contraire des aiguilles d’une montre) ; il est négatif dans le cas contraire.

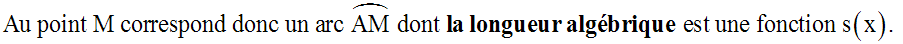
Sur (C), s(x) sera nommée abscisse curviligne de M.

Fixons M et soit un second point M’ de (C) de coordonnées :

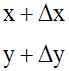
Soient H le pied de la perpendiculaire à [Mt) abaissée de M’ et a la mesure, en radian, de l’angle orienté
{[Mt) , [MM')}.

On a la double inégalité suivante :

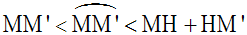
Or, MH = MM’ . cosa et HM’ = MM’ . sina

Donc,

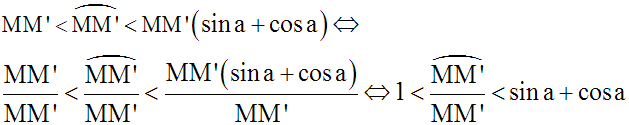
Lorsque M’ tend vers M, a tend vers 0 et (sina + cosa) tend vers 1.

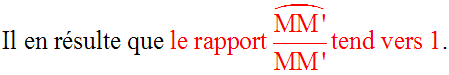
On dira alors qu’un arc et sa corde sont deux infiniment petits équivalents.

Le théorème de Pythagore donne :

Donc :

Ce qui donne :

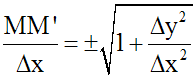
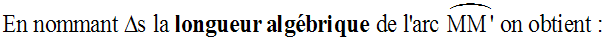
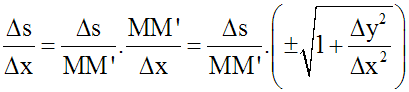
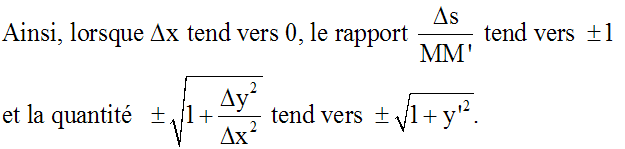
Il en résulte que :

Cette formule donne la différentielle ds d’un arc de le courbe (C) d’équation y = f(x) :

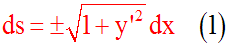
En élevant au carré les deux membres de (1), on obtient :

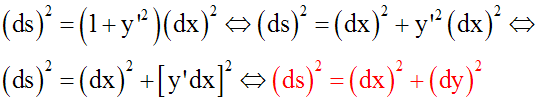
Cette dernière formule sera utile lorsque x et y sont des fonctions d’un paramètre réel, par exemple t.

En effet dans ce cas on peut écrire :

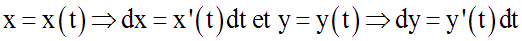
Et, par suite :

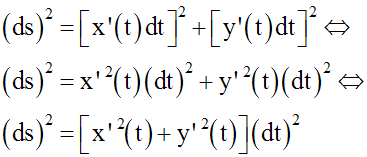
Et ainsi :

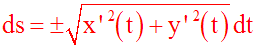
En passant à la somme, on obtient les cas suivants :

1^er cas : en coordonnées cartésiennes

M (x , y) étant un second point de (C), on a :

Finalement, on obtient :

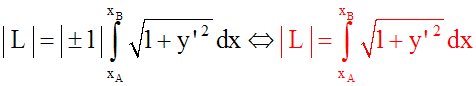
2^ème cas : (C) est définie paramétriquement par les équations x = x(t) et y = y(t)

Finalement, on obtient :

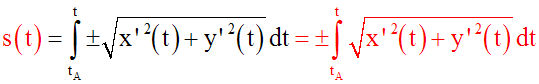
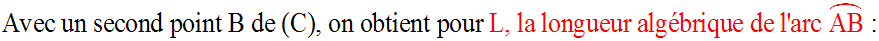
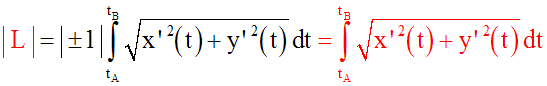
Application

Calcul du périmètre du cercle

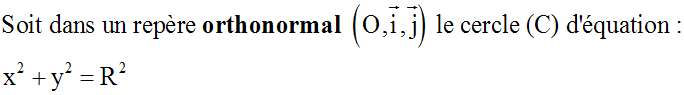
On se propose de calculer son périmètre.

Soient A (R , 0) et B (0 , R) les intersections de (C) respectivement avec l’axe des abscisses et l’axe des ordonnées.

Si L est la longueur algébrique de son premier quart, alors le périmètre de (C) sera 4L.

Soit M(x ; y) un point quelconque de ce premier quart de (C).

On sait que x = R . cost et y = R . sint

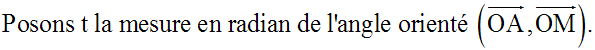
Ce qui donne :

Donc,

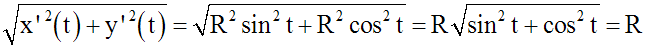
On obtient finalement :

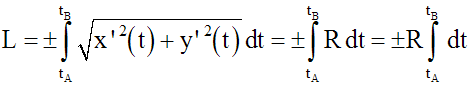
Or, on a :

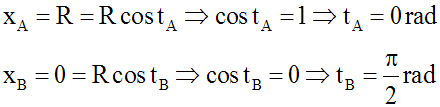
On obtient finalement :

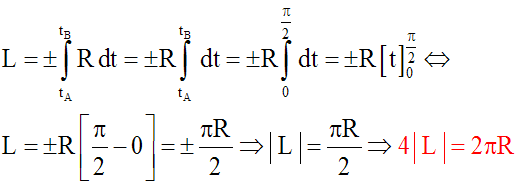
2- Calcul de la surface engendrée par la rotation d'une portion de courbe (C) non fermée autour d'un axe (d)
[(d) située dans le plan de (C) et cette portion de courbe (C) rencontrant (d) au plus en un point]

On suppose d'abord que (C) représente une certaine fonction numérique y = f(x) intégrable sur son domaine de définition Dom(f), projeté orthogonal de (C) sur (d).

Par ailleurs, la portion de (C) a pour extrémités les points A et B.

Le repère, considéré comme orthonormal, a son origine O sur (d).

L' axe des abscisses est (d) dont le sens est fixé.

L'axe des ordonnées est la droite passant par O, située dans le plan de (C) et perpendiculaire à (d), le sens positif étant également fixé.

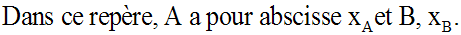
Soient M(x ; y) un point quelconque de la portion de (C) et M ', le second point M' appartenant à cette portion, d'abscisse (x + dx).

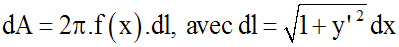
Ainsi, en intégrant cette équation différentielle entre les points x_A et x_B, on obtient l'aire latérale engendrée par la portion de(C) dans sa rotation complète autour de (d).

Si A est cette aire, alors on a :

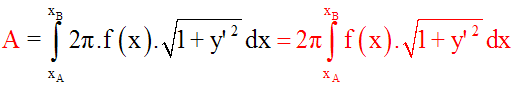
Cas où (C) est définie paramétriquement

Dans ce cas on a :

x = x(t) et y = y(t)

Ainsi, en intégrant cette équation différentielle entre les points t_A et t_B, t_A et t_B étant les valeurs de t pour lesquelles x(t_A) = x_A et x(t_B) = x_B, on obtient l'aire latérale engendrée par la portion de courbe (C) dans sa rotation complète autour de (d).

A étant cette aire, alors :

Applications

A-

On donne dans un repère orthonormal (x'x , y'y) un segment de droite (L) d'équation
y = 2 x limité par ses deux points extrémités A (ici, A est l'origine du repère) et B d'abscisses
respectives 0 et 3.
On demande de calculer l'aire latérale engendrée par une rotation complète de (L) autour
de l'axe des abscisses x'x.

La surface S engendrée par la rotation complète de (L) autour de x'x est égale à :

(ici u . a est l'unité de mesure d'aire)

B-

Calcul de la surface d'un sphère

On donne dans un repère orthonormal (x'x , y'y) le 1er quart de cercle (Q) d'équation :

Il est limité par les points A(0 , R) et B(R , 0).

La surface S de la sphère (S) de centre O et de rayon R sera donc le double de celle engendrée par la rotation complète de (Q) autour de l'axe des abscisses.

L'équation de la courbe limitée par A et B est :

On a donc :

Ainsi, on a :

On obtient finalement :

Remarque :

On trouvera le même résultat si (Q) est défini paramétriquement.

3- Calcul du volume engendré par la rotation d'une portion de surface autour d'un axe

On donne, dans un repère orthonormal (x'x,y'y), une fonction numérique f définie et positive sur l'intervalle [a , b]; a < b.

Soit D l'ensemble des points M(x , y) tels que :

Soient m(x , 0) et m'(x+dx, 0) deux points très voisins de l'axe des abscisses, tous deux ayant leurs abscisses appartenant à [a , b].

Les parallèles à l'axe des ordonnées menées de m et m' rencontrent la courbe (C) d'équation
y = f(x) respectivement aux points M(x , y) et M'(x+dx , y+dy).

L'élément (m m' M' M), assimilé à un rectangle, a pour dimensions :
dx et y.

(m m' M' M) faisant un tour complet autour de l'axe des abscisses, engendrera un élément cylindrique
de volume dV égal à :

Le passage à la somme sur l'intervalle [a , b] donnera le volume V du solide engendré par la rotation complète autour de l'axe des abscisses de la surface limitée par l'ensemble D.

Ainsi, on obtient :

Application

Volume de la sphère

On donne dans un repère orthonormal (x'x , y'y) le 1er quart de cercle (Q) d'équation :

Il est limité par les points A(0 , R) et B(R , 0).

Le volume V de la sphère de centre O et de rayon R sera donc le double du volume engendré par la rotation complète autour de l'axe des abscisses de la surface (OAB).

L'équation de la courbe limitée par A et B est :

On a donc :

retour au sommaire