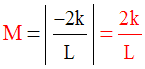Application de l'intégrale au calcul de masses, de moments d'inertie et à la détermination de centres de gravité - Première partie
Il s'agit là de l'application de l'intégrale aux divers calculs portant sur des plaques assimilées à des surfaces planes (faible épaisseur) et sur des barres assimilées à des courbes planes ou à des segments de droite (faible épaisseur)
1- Les hypothèses de calcul
La plaque assimilée à une surface plane aura une épaisseur négligeable par rapport aux autres dimensions.
La barre assimilée à une portion de courbe plane aura également une épaisseur négligeable par rapport à sa longueur.
2- Notions de masse spécifique
Masse spécifique superficielle en un point d'une plaque
Soit une plaque (P) et soit un point quelconque M(x , y) de cette plaque rapportée à un repère orthonormal :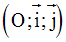
Soit autour de M un élément de surface
DS
et soit
Dm
la masse de cet élément.
On
appellera masse spécifique
superficielle moyenne de cet élément la quantité :
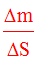
Si, lorsque DS tend vers zéro, la limite finie de ce rapport
existe alors on la notera p (p réel strictement positif et fini) et on écrira :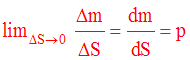
p sera appelée masse spécifique
superficielle de la plaque (P) au point M.
p est donc une fonction numérique dépendant de la position de
M.
Lorsque p varie avec le point M, on dira alors que la
plaque est hétérogène.
Lorsque p est une constante,
alors on dira que la plaque est
homogène.
Masse spécifique linéaire en un point d'une barre
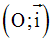
Soit autour de M un élément d'arc
Dl
et soit
Dm
la masse de cet élément.
On appellera masse spécifique
linéaire moyenne de cet élément la quantité :
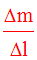
Si, lorsque Dl tend vers zéro, la limite finie de ce rapport existe alors on la notera q (q réel strictement positif et fini) et on écrira :
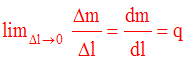
q sera appelée masse spécifique
linéaire de la barre (B) au point M.
q est donc une fonction numérique dépendant de la position de
M.
Lorsque q varie avec le point M, on dira alors que
la barre est hétérogène.
Lorsque q est une constante,
alors on dira que la barre est homogène.
Ces définitions et résultats s'appliquent en particulier aux barres rectilignes.
3- Masse d'une plaque dont le contour est assimilé à l'ensemble des courbes suivantes rapportées à un repère plan orthonormal :
- (C) représentative d'une fonction numérique positive f définie aux points a = xA ³ 0 et b = xB > a, A et B étant les extrémités de (C)
- les droites x = a et x = b parallèles à l'axe des ordonnées
La
masse spécifique superficielle p en un point M(x , y) quelconque
lui appartenant est proportionnelle à x :
p(x) = k x, k réel strictement
positif et constant.
On
suppose que les droites x = a et x = b coupent l'axe des
abscisses aux points A' et B'.
Ainsi la plaque est assimilée à la surface limitée par la courbe
fermée (A A' B' B).
Soit m(x , 0) un point quelconque de cette plaque tel que a
£
x £
b.
Les droites parallèles à l'axe des ordonnées, menées par m et m' rencontrent (C) respectivement aux points M(x , y),
avec y = f(x) et M'(x + dx , y + dy).
L'élément de surface (m m' M' M) peut être assimilé à un
rectangle dont la surface est :
ds = y . dx = f(x) dx
dx étant infiniment petit, la masse spécifique
superficielle p(x) de cet élément peut être considérée
constante en tout point de cet élément.
Si dm est la mase de cet élément, alors on a :
dm = p(x) . ds = k x . f(x) dx
Le passage à la somme donnera la masse
M de la plaque :
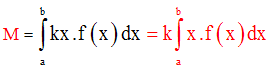
Application
Calcule la masse M d'un disque de centre O et de rayon R.
On suppose que la masse spécifique superficielle p en un point M
quelconque du disque est proportionnelle à la distance du
point à un diamètre déterminé de ce disque.
Réponse :
Si on pose p = K x, avec K réel strictement positif et constant, on trouvera :
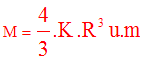
( Ici, " 1 u . m " se lit " une unité de masse ")
Le repère rectiligne d'origine
O a pour support celui de la barre rectiligne [AB].
A (a) et B (b) tels que 0 £ a < b sont les deux extrémités de cette barre.
Soit m(x) un point quelconque de cette barre; donc a
£
x £
b.
Soit le point m'(x + dx)
appartenant à [a , b].
Soit p(x) la masse spécifique linéaire de cette barre au point
m.
L'élément [m m'] a pour mesure algébrique dx. Or, dx
étant infiniment petit, on peut considérer que p(x) est
constant en tout point de [m m'].
Ainsi, si dM est la masse (comptée algébriquement) de [m
m'], alors :
dM = p(x) . dx
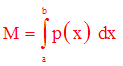
La masse de cette barre s'écrit alors :
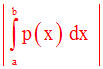
Application
Un corps est assimilé à un segment de droite de longueur 2 L.
On suppose que la masse spécifique linéaire en un point
quelconque du segment est inversement proportionnelle au
carré de la distance du point au milieu du segment.
On demande de calculer la masse de ce corps.
Soit [AB] ce segment et O son milieu.
A est pris comme origine du repère normé :

Le
corps étant rapporté à ce repère, on a :
xA = 0 et xB
= + 2 L
Soit m(x) un point quelconque de [AB] et le point voisin m' (x +
dx).
La relation de Chasles permet d'écrire :
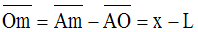
L'élément
[mm'] a pour longueur dx infiniment petit; donc la masse
spécifique linéaire en tout point de cet élément peut être
considérée constante.
On a donc :

Ainsi, si dM est la masse (comptée algébriquement) de cet élément, alors :
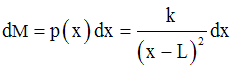
Le passage à la somme donnera :
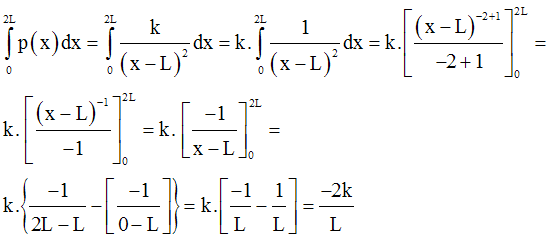
La masse M de ce corps sera donc :