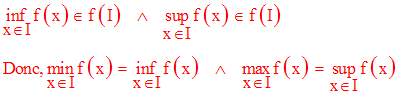
Les bornes inférieure et supérieure de f appartiennent à Im(f) = f (I) :
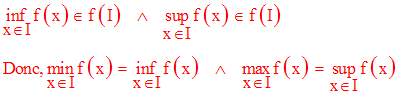
Dérivabilité et notion de différentielle d'une fonction numérique - 1ère partie
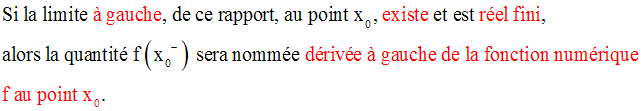
Soit a0 un réel quelconque de I.
On donne une fonction numérique f définie et dérivable sur un intervalle réel I.
On représente
graphiquement f dans un repère orthonormal.
Sa courbe représentative est (C).
Soit A le point appartenant à (C) et ayant pour abscisse a0.
Soit M un point courant de (C) d’abscisse x.
a et m sont les projetés orthogonaux de A et M sur l’axe des abscisses.
Du point A menons la perpendiculaire à (Mm) qui rencontre cette dernière au point H.
Du point A menons la tangente [At à (C) qui rencontre (Mm) au point B.
On a :

Dérivabilité et notion de différentielle d'une fonction numérique - 3ème partie
On a :
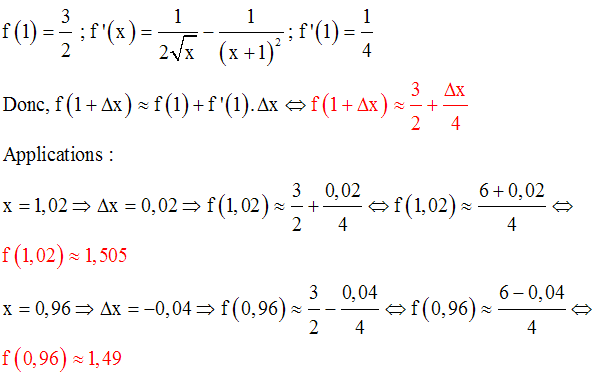
Intégrabilité d'une fonction numérique - Applications - 1ère partie
On a :
