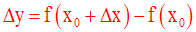
DERIVABILITE ET NOTION DE DIFFERENTIELLE
D’UNE FONCTION NUMERIQUE

1- Dérivées en un point d’une fonction numérique

Soit f une fonction numérique définie sur un intervalle ouvert I de R et soit x₀ un point quelconque de I.

On fait varier la quantité x₀ d’une quantité réelle notée Δx de manière que le point réel x = x₀ + Δx ainsi obtenu appartienne à I.

Δx est nommée accroissement de la variable réelle x₀. C’est une quantité qui peut être strictement positive ou strictement négative.

f fait correspondre à (x₀ + Δx) le réel f (x₀ + Δx). 

On a ainsi :

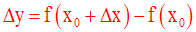
qui sera nommée accroissement de la fonction f (x).

Considérons le rapport :

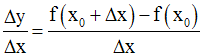
Comme x = x₀ + Δx, Δx = x – x₀,

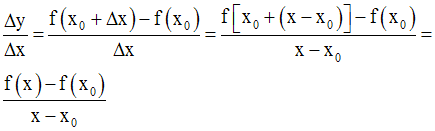
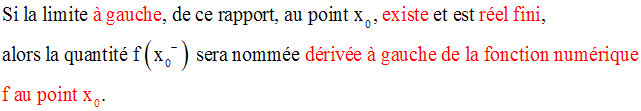
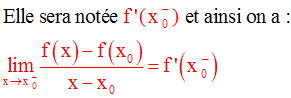
On dira que la fonction numérique f admet une dérivée à gauche au point x₀.

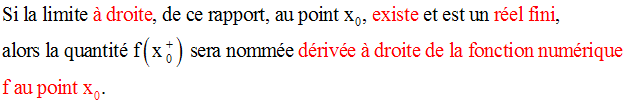
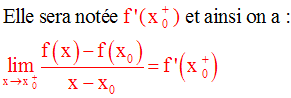
On dira que la fonction numérique f admet une dérivée à droite au point x₀.

Si de plus, au point x₀, les deux dérivées de f, à gauche et à droite, sont égales, alors on dira
que f est dérivable au point x₀.

Dans ce cas, la valeur commune de ces deux dérivées sera notée :

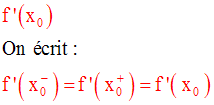
Exemples :

1-

Soit la fonction numérique g définie sur R par :

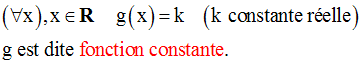
On nous demande de démontrer que g est dérivable en tout point réel x₀.

On forme d’abord le rapport :

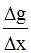
On a :

2-

Soit la fonction numérique h définie sur R par :

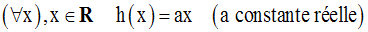
On nous demande de démontrer que h est dérivable en tout point réel x₀.

On forme d’abord le rapport :

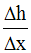
On a :

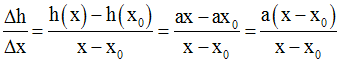
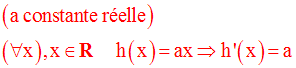
3-

On donne une fonction numérique f définie et dérivable en tout point réel appartenant à un intervalle réel I.

Soit la fonction numérique g définie comme suit :

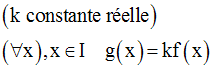
On demande de démontrer que g est dérivable en tout point appartenant à I.

On a :

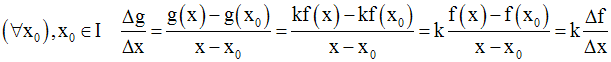
Or, f étant dérivable en tout point x₀ appartenant à I, on a :

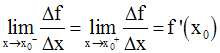
Donc,

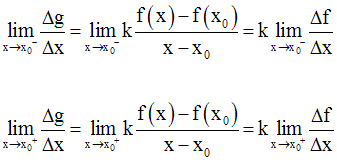
Ainsi,

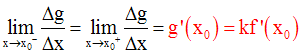
4-

Soit la fonction numérique f définie  par :

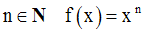
On nous demande de démontrer que f est dérivable en tout point réel x₀ appartenant à son domaine de définition.

On exclut le cas banal où n est nul, puisque, dans ce cas, la fonction devient, sur son domaine de définition R^*,
constante et égale à 1; par conséquent elle est dérivable en tout point réel de son domaine de définition et
sa dérivée est nulle.

f est définie sur R, donc définie en x₀.

On forme d’abord le rapport :

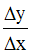
On a :

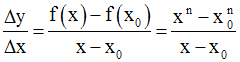
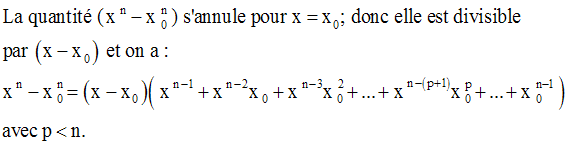
Le rapport s’écrit alors :

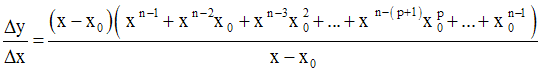
On étudie ensuite les limites de ce rapport, à gauche et à droite, en x₀ .

On sait que :

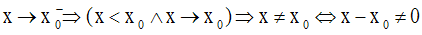
Donc on peut simplifier par (x – x₀) et on obtient :

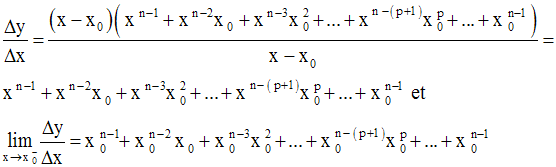
On sait que :

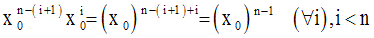
Comme on a n termes de la forme :

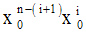
dans l’expression du rapport, alors on obtient finalement :

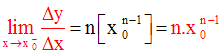
On démontre de la même manière que la limite à droite de ce rapport en x₀ vaut également :

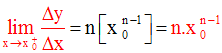
Donc, pour tout réel x₀ , on a :

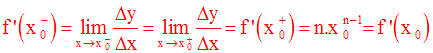
Conclusion :

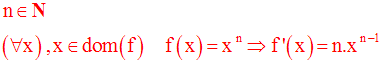
Cette conclusion s’applique également pour n appartenant à l’ensemble des rationnels.

On admettra donc que :

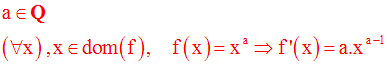
Applications

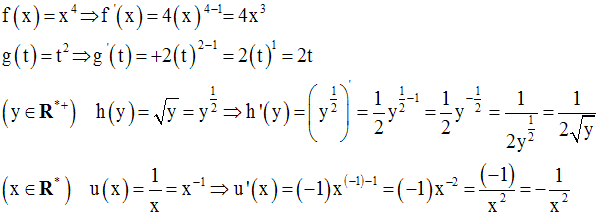
5-

Soit la fonction numérique i définie sur R^* par :

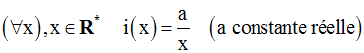
On nous demande de démontrer que i est dérivable en tout point réel non nul x₀.

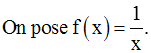
La fonction numérique i peut donc s’écrire :

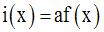
D’après le résultat de l’exemple 3 qui précède, on a :

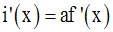
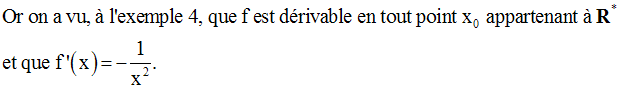
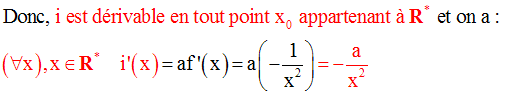
Exercice

Quel est le domaine de définition de f ?

Calcule :

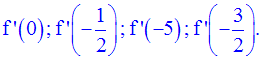
Solution

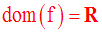
f est dérivable en tout point de R.

On a :

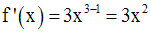
En remplaçant dans cette expression de la fonction dérivée, x par les valeurs données, on obtient :

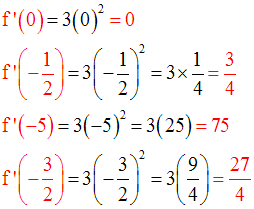
2- Dérivabilité d’une fonction numérique sur un intervalle réel

Soient deux réels finis a et b tels que a < b.
 

Soit f une fonction numérique définie sur un intervalle réel ouvert ]a , b[.

f est dérivable sur ]a , b[ si et seulement si elle est dérivable en tout point de ]a , b[.

Soit f une fonction numérique définie sur un intervalle réel fermé [a , b].

f est dérivable sur [a , b] si et seulement si :

elle est dérivable en tout point de ]a , b[ ;

elle est dérivable à droite au point a ;

elle est dérivable à gauche au point b.

Exercice

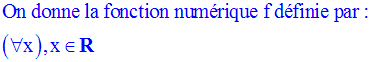
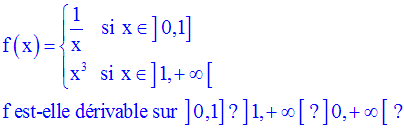
Solution

Dans chacun des trois intervalles d’étude, on forme le rapport :

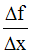
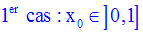
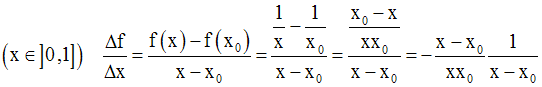
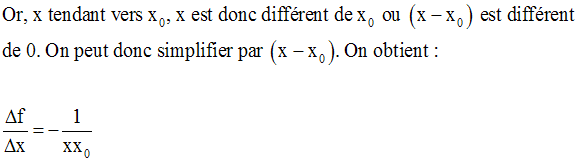
Ainsi,

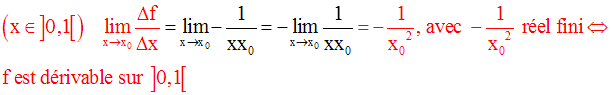
De plus,

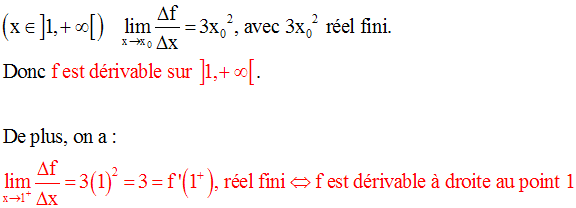
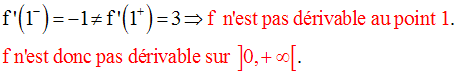
3- Interprétation géométrique de la dérivée d’une fonction numérique en un point réel fini

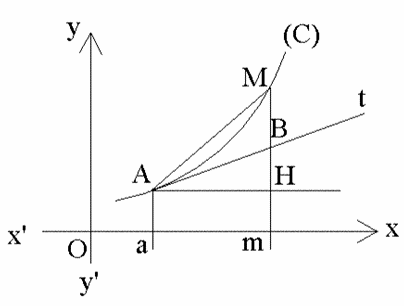
Soit a₀ un réel quelconque de I.

Exemple

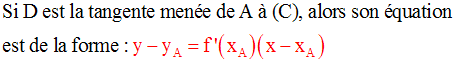
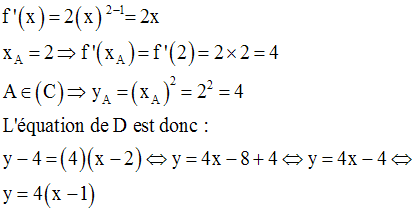
Exercice

On donne la fonction numérique f définie par :

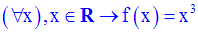
(C) est sa courbe représentative dans un repère orthonormal.

Etablis l’équation de la tangente D à (C), issue du point A de (C) d’abscisse – 2.

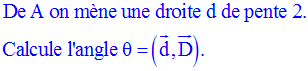
Solution
 

Equation de la tangente D à (C), issue du point A de (C) d’abscisse – 2

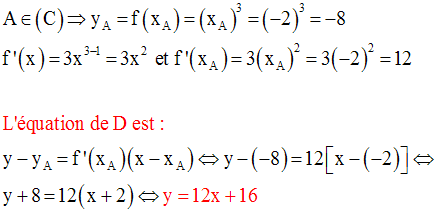
4- Continuité et dérivabilité d’une fonction numérique

Une fonction numérique f dérivable en un point a de son domaine de définition, est continue en ce point.

La réciproque est fausse.

Démonstration

Soit f dérivable au point réel a appartenant à I = dom (f).

La limite de f en a est définie et est égale à f ^’ (a), réel fini.

On a par hypothèse :

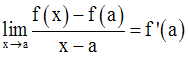
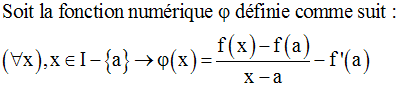
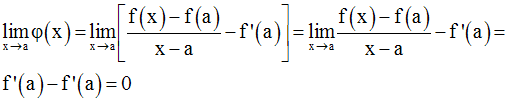
Or, comme la quantité x – a est différente de 0 (car x appartient à I – {a}),

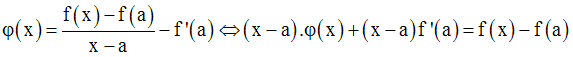
Donc,

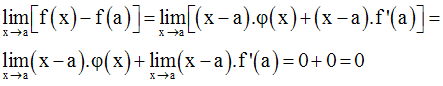
Ainsi, on a finalement :

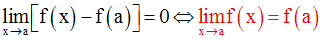
Ce qui implique que f est continue au point a.

La réciproque est fausse ; pour le démontrer, il suffit de trouver une fonction numérique continue en un point réel
de son domaine et non dérivable en ce point.

Soit la fonction numérique g définie par :

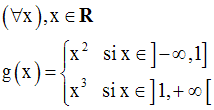
On a :

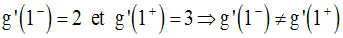
Donc g n’est pas dérivable en 1.

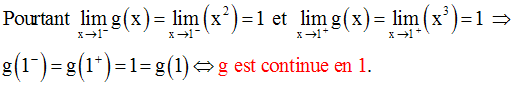
Dérivabilité et continuité d’une fonction numérique sur un intervalle de R

Une fonction numérique f dérivable en tout point d’un intervalle réel est continue en ces points ; donc on a le résultat suivant :

Une fonction numérique f dérivable sur un intervalle réel I est continue sur cet intervalle.

La réciproque est fausse.

Exercice

Solution

Au point 0, on a :

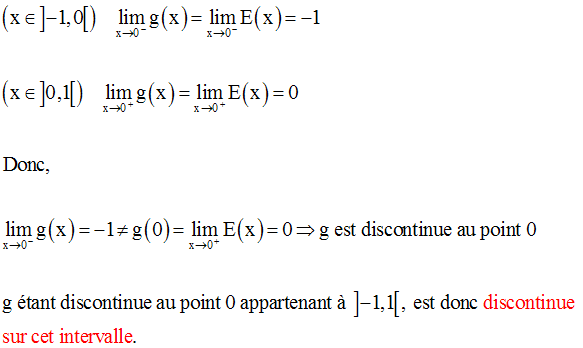
Au point 2, on a :

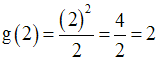
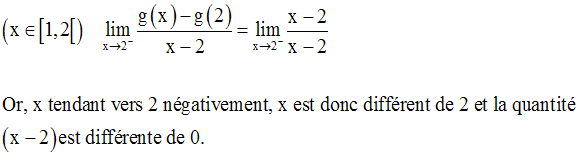
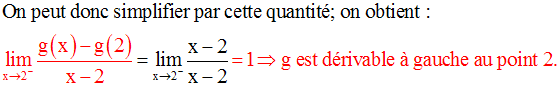
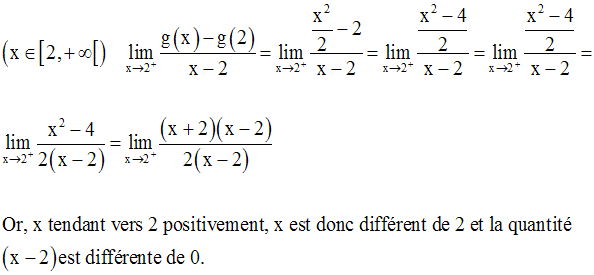
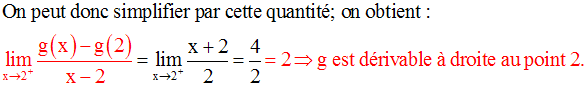
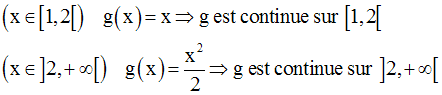
Au point 2, on a :

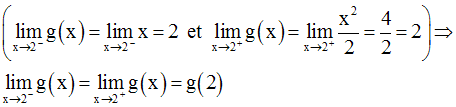
g est donc continue au point 2.

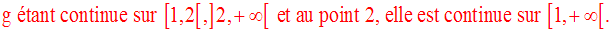
5- Dérivée d’une fonction numérique réciproque

Soit f une fonction numérique continue et strictement monotone sur un intervalle réel [a , b].

On sait que f est un homéomorphisme de [a , b] sur [f(a) , f(b)] et admet une fonction numérique réciproque
f ^-1 qui est également un homéomorphisme de [f(a) , f(b)] sur [a , b].

Supposons que f est dérivable en x₀ appartenant à  [a , b] et que la valeur f ’(x₀) n’est pas nulle.

Posons f (x₀) = y₀ .

On a, du fait des homéomorphismes :

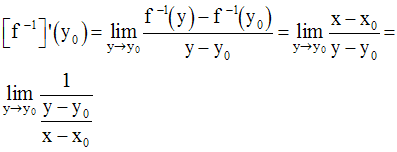
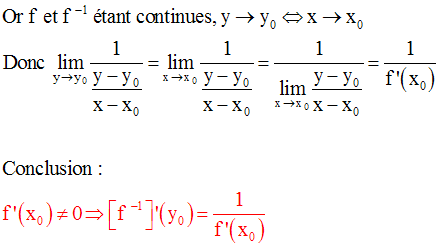
Exemple :

La fonction numérique f définie comme suit :

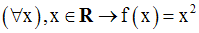
est continue et strictement croissante sur l’intervalle réel ]0 , + ∞[.

f est un homéomorphisme sur ]0 , + ∞[ et admet une fonction réciproque f ^-1 continue et strictement
croissante sur l’intervalle réel ]0 , + ∞[.

On a :

Exercice

On donne la fonction numérique h définie par :

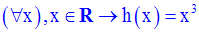
Démontre que h est un homéomorphisme sur [0 , + ∞[.

Définis sa réciproque h ^-1 et calcule :

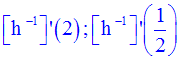
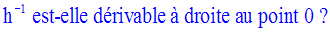
Solution

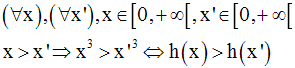
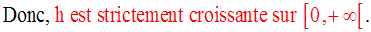
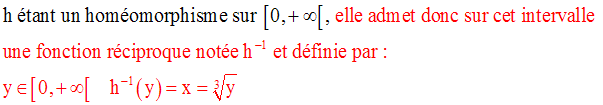
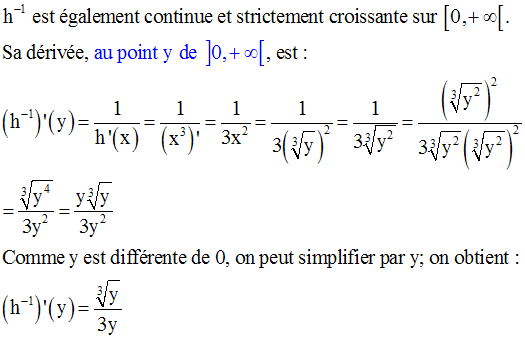
En particulier, on a :

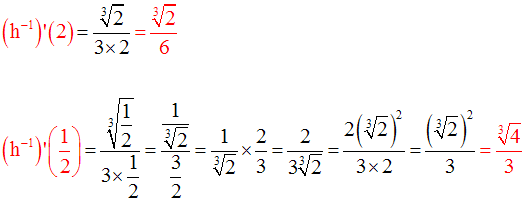
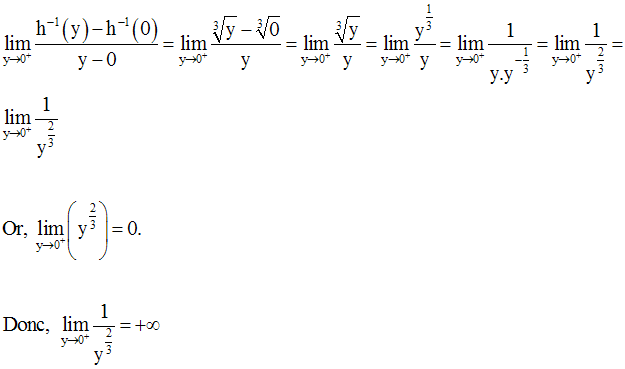
6- Dérivée d’une fonction numérique composée

Soit f une fonction numérique définie et dérivable sur l’intervalle I.

Soit g une fonction numérique définie et dérivable sur l’intervalle J.

Supposons que l’on a :

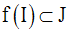
Soit x₀ un élément quelconque de I. f (x₀) appartient à J.

On a :

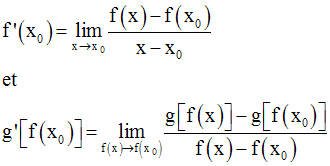
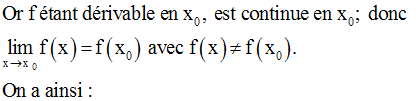
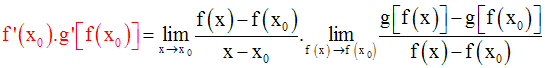
f étant continue au point x₀ , alors :

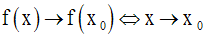
On a donc :

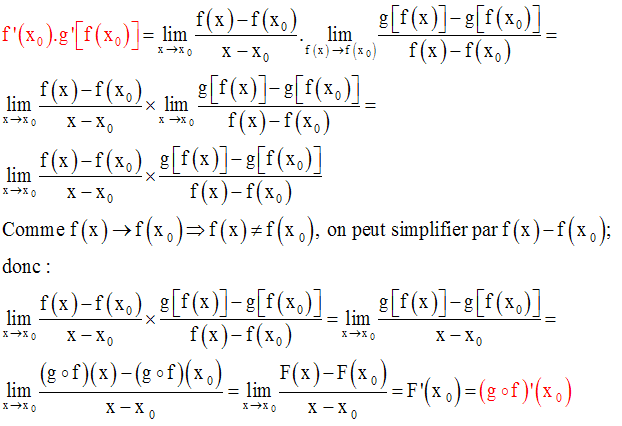
Conclusion :

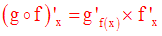
Exemple :

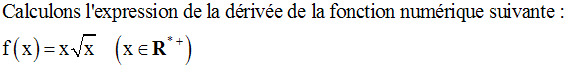
Nous avons :

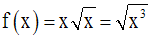
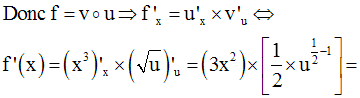
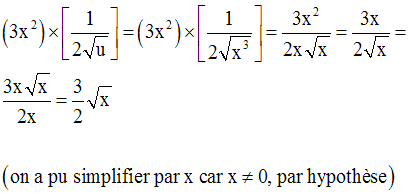
7- Opérations sur les dérivées

On a démontré plus haut que :

La dérivée d’une fonction numérique constante est nulle.
 

La dérivée de la fonction numérique définie par :

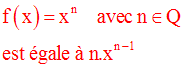
f étant une fonction numérique dérivable sur un intervalle I, la dérivée de k.f,

k étant un réel constant est égale k.f ’.

Autres propriétés

On sait que la limite d’une somme de fonctions numériques est égale à la somme des limites de
ces fonctions, et on sait que la dérivée d’une fonction numérique dérivable est elle-même une
fonction numérique.

Donc on a la propriété suivante :

La dérivée d’une somme de fonctions numériques dérivables sur un intervalle réel I est égale à la
somme des dérivées de ces fonctions numériques.

Application

La dérivée de la fonction numérique « polynôme » f  définie par :

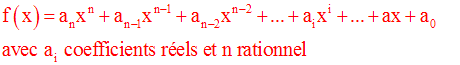
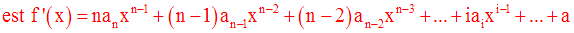
Exemple :

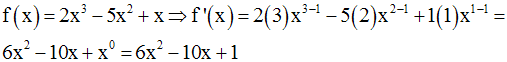
Soient deux fonctions numériques u et v dérivables sur un intervalle I.

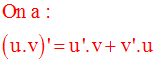
Démonstration

On pose F = u.v

On sait que :

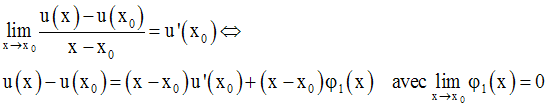
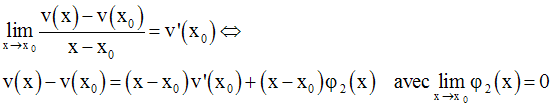
On a donc :

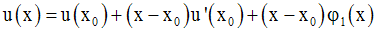
et

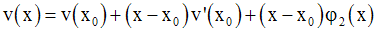
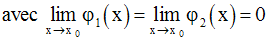
On multiplie membre à membre :

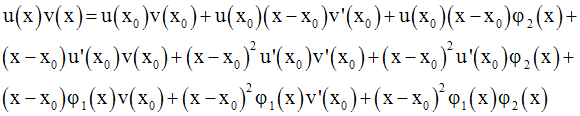
Tous les termes du second membre contenant un facteur de la forme :

tendent vers 0 lorsque x tend vers x₀.

De plus x tendant vers x₀ , x est différent de x₀  ou (x − x₀ ) ≠ 0 et on peut donc diviser les
deux membres par (x − x₀ ) :

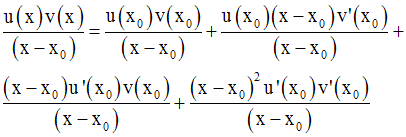
et en simplifiant par (x – x₀) :

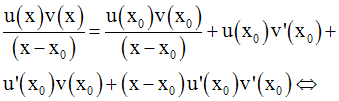
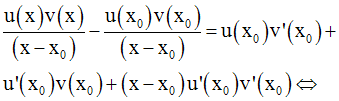
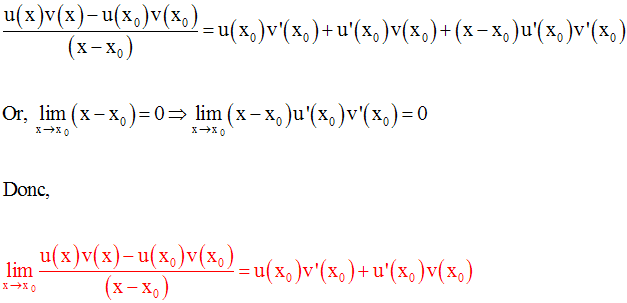
Conclusion :

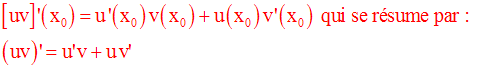
Cette conclusion s’étend à un produit quelconque de fonctions numériques dérivables sur
un intervalle réel I :

Exemple :

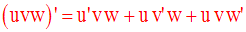
Elle s’étend également à un produit quelconque de fonctions numériques dérivables sur un intervalle réel I,
toutes égales à u :

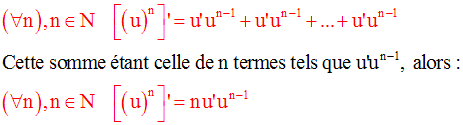
On admettra que cette dernière propriété s’applique également dans le cas où n est rationnel.

Exemples

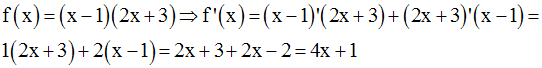
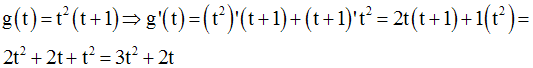
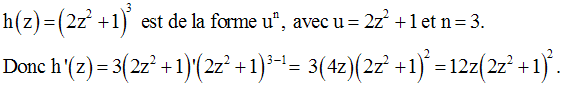
Par la même méthode utilisée pour le calcul de la dérivée de u.v, on peut facilement démontrer que :

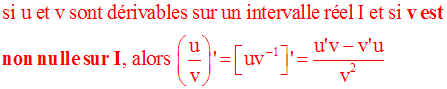
Exemple :

Exercice

Après avoir déterminé le domaine de définition de chacune des fonctions numériques suivantes,
calcule l’expression générale de sa dérivée :

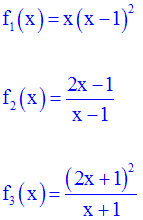
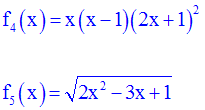
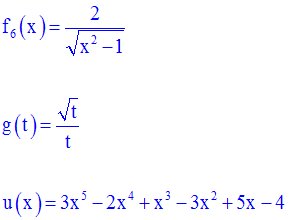
Solution

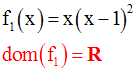
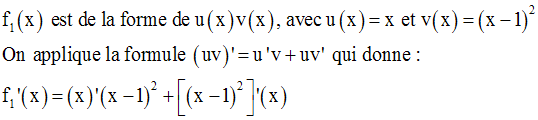
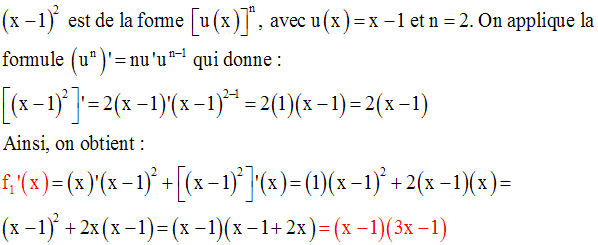
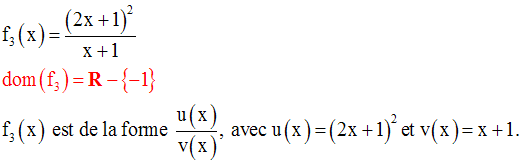
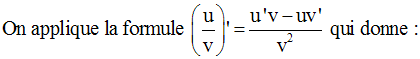
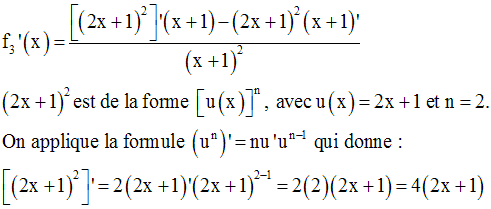
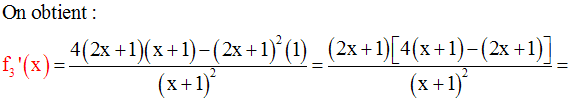
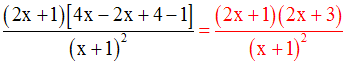
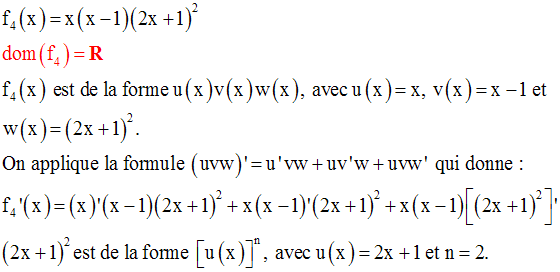
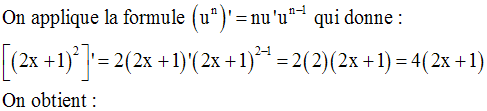
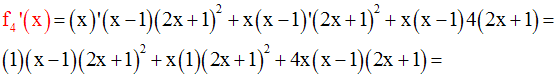
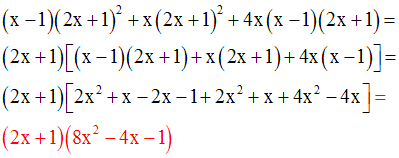
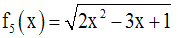
La racine carrée d’un réel strictement négatif n’étant pas définie dans R, la quantité sous le radical
devra être largement positive.

Or, cette quantité est un trinôme du second degré en x dont le coefficient a est égal à 2.

On doit donc trouver l’ensemble des réels x qui le rendent de même signe que celui de a.

Pour cela, on calcule d’abord son discriminant.

On a :

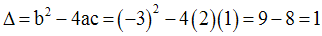
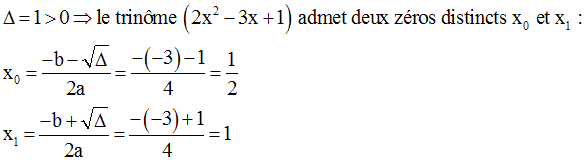
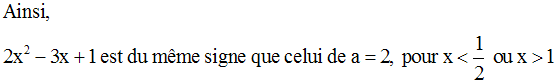
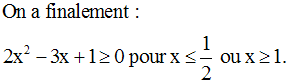
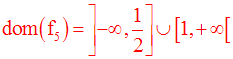
Remarque

On aurait pu trouver facilement les zéros de ce trinôme car la somme de ses coefficients étant nulle,
un des zéros est égal à 1, l’autre se calcule en remarquant que le produit des zéros est la quantité :

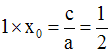
On en déduit la valeur de x₀.

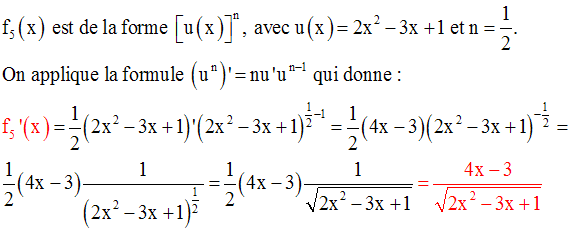
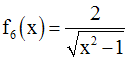
La racine carrée d’un réel strictement négatif n’étant pas définie dans R, la quantité sous le radical
devra être largement positive.

De plus le dénominateur devra être différent de 0.

Or, la quantité sous le radical est un trinôme du second degré en x dont le coefficient a est égal à 1.

Ce trinôme peut se mettre sous la forme :

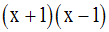
Ses zéros sont :

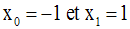
Ainsi, il est de même signe que celui de son coefficient a qui vaut 1, pour :

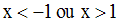
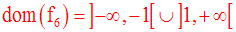
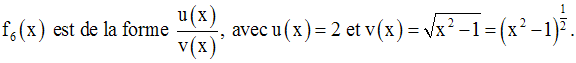
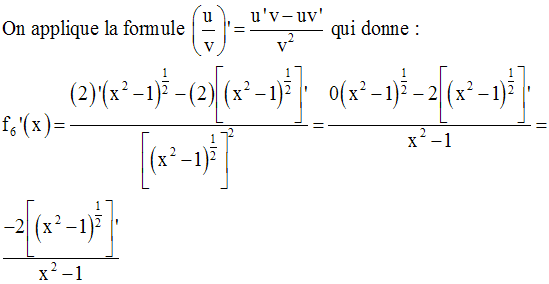
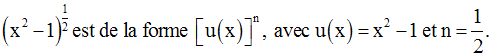
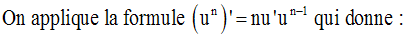
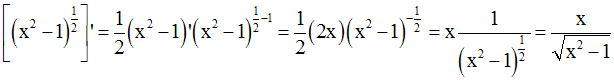
On obtient :

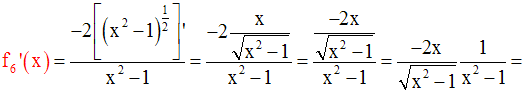
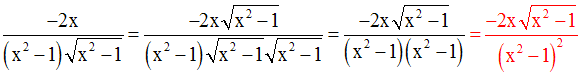
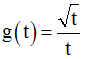
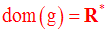
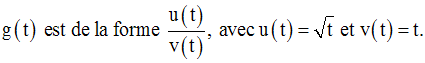
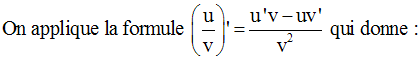
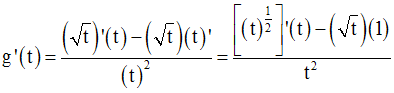
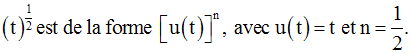
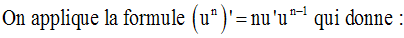
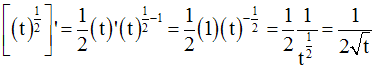
On obtient :

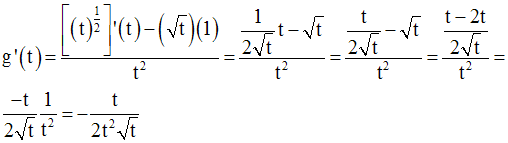
Comme t est différent de 0, on peut simplifier par t ; on obtient :

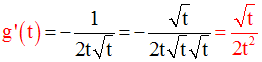
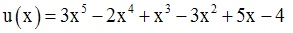
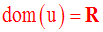
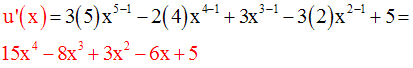
8- Fonction dérivée - Dérivées successives

Soit f une fonction dérivable sur un intervalle I.

Sa dérivée est définie en tout point de I : pour tout réel x de I, il existe une valeur réelle et une seule f ’(x).

Donc f ’ est une fonction numérique définie sur I. On l’appelle fonction dérivée.

f ’ peut à son tour être dérivable sur I ; sa dérivée sera dans ce cas notée :

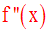
On l’appelle dérivée seconde de f.

D’une manière générale, si la nième dérivée de f existe, alors elle sera notée :

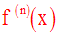
On l’appelle dérivée nième de f.

Définition

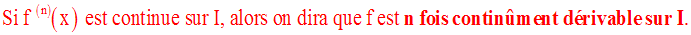
Exemple :

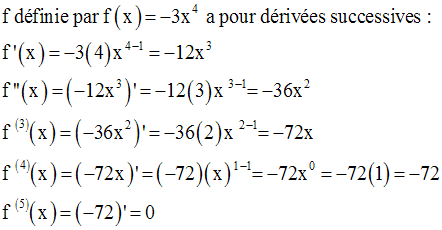
9- Dérivées des fonction circulaires usuelles

Dérivée des  fonctions sinus et cosinus

Rappel d’une formule trigonométrique :

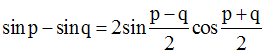
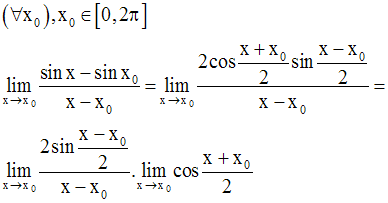
Or :

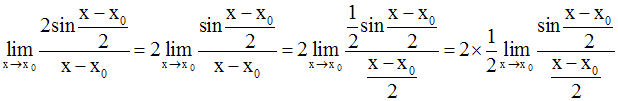
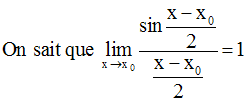
(la démonstration de ce résultat est donnée en exercice, à la fin de ce cours)

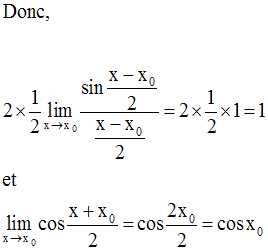
On obtient ainsi :

Et finalement :

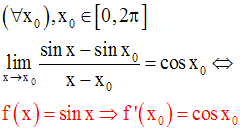
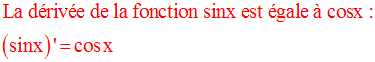
On peut, par la même méthode, démontrer le résultat suivant :

Dérivée des  fonctions tangente et cotangente

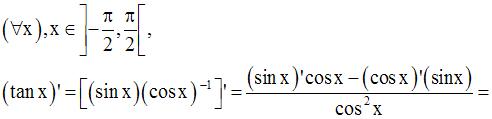
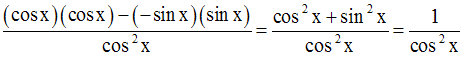
Conclusion :

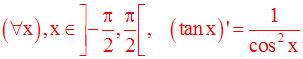
On peut par la même méthode démontrer que :

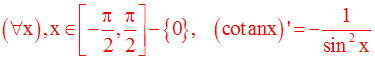
Exemples

Exercice

Dans le domaine de définition de chacune des fonctions numériques suivantes, calcule
l’expression générale de sa dérivée :

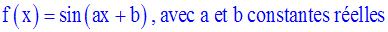
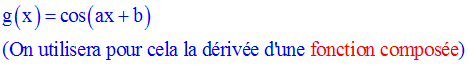
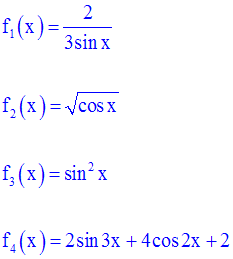
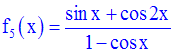
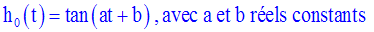
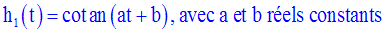
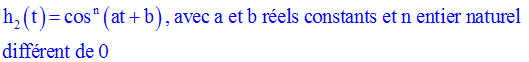
Solution
 

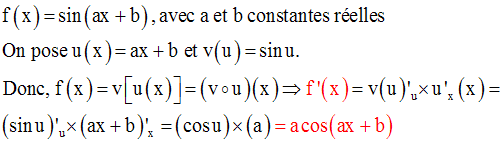
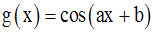
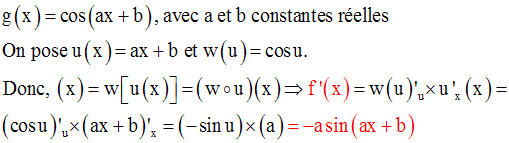
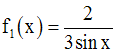
Le dénominateur devra être non nul ; donc :

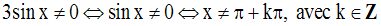
Ainsi, on a :

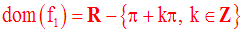
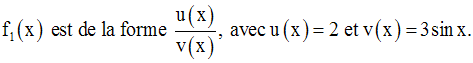
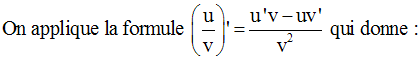
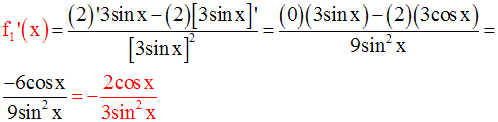
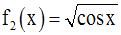
La racine carrée d’un réel strictement négatif n’étant pas définie dans R, la quantité sous le radical
devra être largement positive.

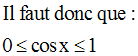
Les solutions générales sont :

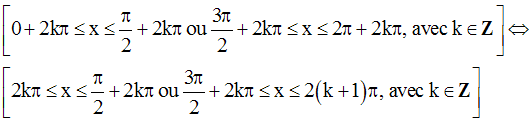
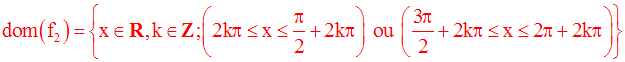
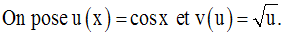
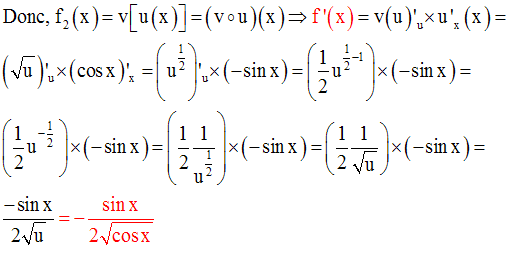
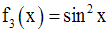
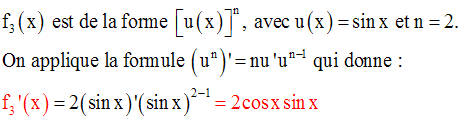
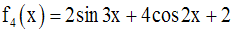
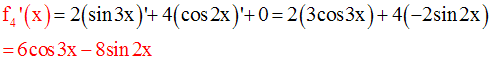
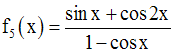
Le dénominateur devra être non nul ; donc il faut que :

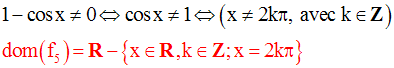
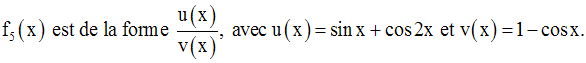
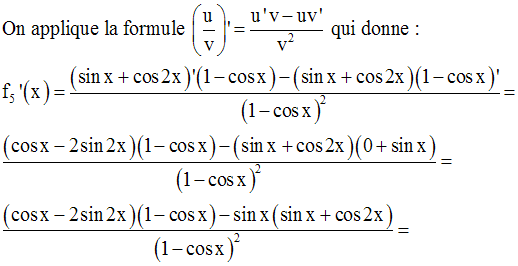
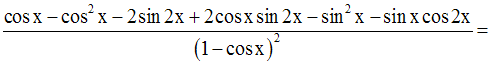
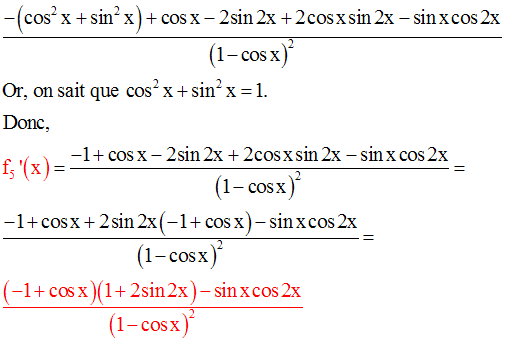
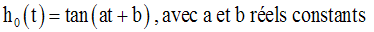
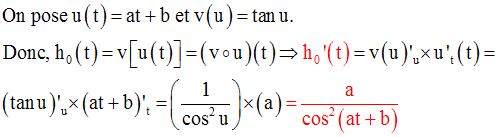
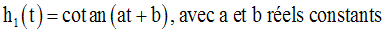
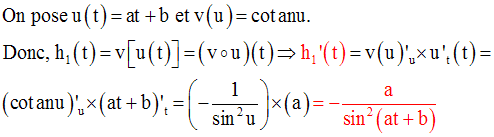
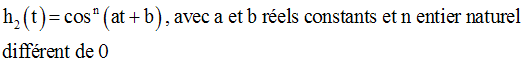
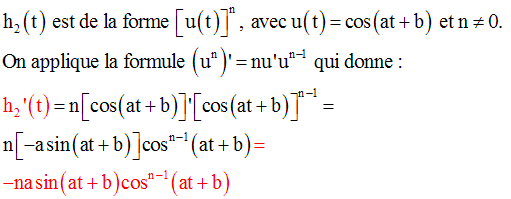
10- Dérivée et monotonie d’une fonction numérique

Dans tout ce qui suit on admettra sans démonstration les théorèmes énoncés.

 On prendra les fonctions numériques f et g dérivables sur un intervalle réel I

Si la dérivée de f est largement positive sur I alors f est croissante sur I.
 

Si la dérivée de f est strictement positive sur I, alors f est strictement croissante sur I.
 

Si la dérivée de f est largement négative sur I alors f est décroissante sur I.
 

Si la dérivée de f est strictement négative sur I, alors f est strictement décroissante sur I.
 

Si la dérivée de f est nulle sur I alors f est une fonction constante sur I.
 

Si f et g ont même dérivée sur I, alors (f – g) et (g – f) sont des fonctions numériques constantes sur I.
 

Supposons I  égal à un intervalle réel fermé [a , b],

avec a < b et soit x₀ un élément de [a , b], avec a < x₀ < b.

Si f est croissante sur [a , x₀ ] et décroissante sur [x₀ , b], et si f(x₀) est un maximum pour f sur I,
alors f ’(x₀) est nulle.

Si f est décroissante sur [a , x₀ ] et croissante sur [x₀ , b], et si f(x₀) est un minimum pour f sur I,
alors f ’(x₀) est nulle.

Remarques importantes 

1)

Les réciproques des deux derniers théorèmes ci-dessus sont fausses.

Par exemple, la fonction numérique f(x) = x³ est dérivable sur R ; de plus f ’(0) = 0.
Cependant f(0) ne présente pas un extremum pour f sur R.

Cette première remarque est très importante ; ne pas en tenir compte constitue une faute grave en Mathématiques et peut être une des causes principales d’échec dans une épreuve ou un concours.

2)

Il faut toujours s’assurer que f est dérivable sur [a , b], car on peut rencontrer une fonction numérique
continue sur [a , b], croissante (resp.décroissante) sur [a , x₀ ], décroissante (resp.croissante) sur [x₀ , b],
présentant un extremum en x₀ avec f ’(x₀) non définie.

Par exemple, la fonction numérique f définie par :

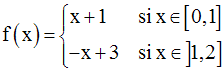
11- Fonction convexe

Définitions

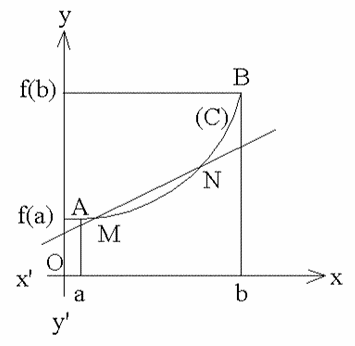
figure 1 : f est convexe sur [a , b]

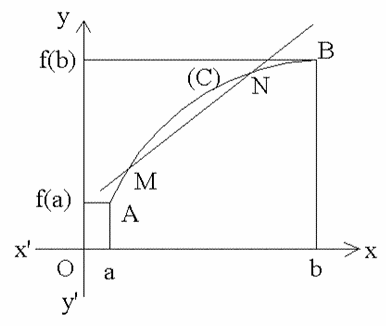
figure 2 : f est concave sur [a , b]

On admettra les théorèmes suivants :
 

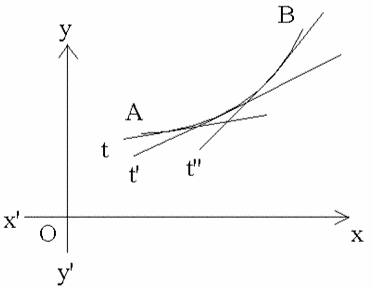
figure 3

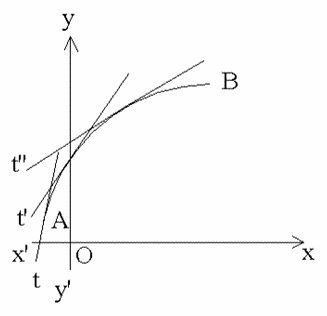
figure 4

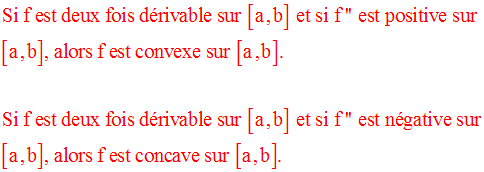
Point d’inflexion

Si f est dérivable sur [a , b] et si x₀  appartenant à [a , b] est tel que f soit convexe (resp. concave) sur
[a , x₀] et concave (resp. convexe) sur [x₀ ,b], alors le point M₀ de (C) d’abscisse x₀ est appelé
point d’inflexion de (C).

La tangente en M₀ à (C) « traverse (C) ».

Il s’ensuit que :

Si f est deux fois dérivable sur [a , b], les réels appartenant à cet intervalle et pour lesquels la dérivée
seconde s’annule en changeant de signe sont les abscisses des points d’inflexion.

Remarque

Par extension, les théorèmes abordés précédemment s’étendent aux cas d’un intervalle ouvert, fini ou infini.

12- Différentielle – Fonctions différentiables

Définition

Soit f une fonction numérique définie sur un intervalle ouvert I contenant le réel x₀.

Théorème

Démonstration

D’après la définition de la différentiabilité, pour que f soit différentiable en x₀ il faut et il suffit qu’il
existe un réel fini a et une fonction numérique ε(x), tels que :

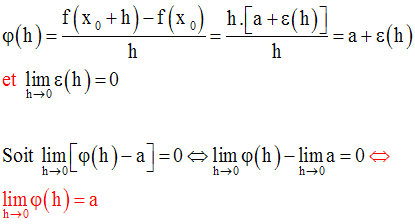
On dira que f est différentiable sur I si et seulement si f est différentiable en tout point de I.

Notation différentielle

Soit la fonction Identité Id(x) = x.

Elle est définie sur R.

Elle est différentiable sur tout intervalle réel ouvert I contenant x₀ fixé.

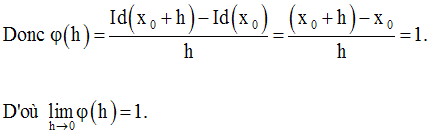
La différentielle de cette fonction au point x₀ est donc d(Id) = 1.h = h.

Puisque Id(x) = x, on convient de noter dx cette différentielle.

D’où dx = h.

En conséquence, la différentielle d’une fonction numérique différentiable au point x₀ se note définitivement :

df = a.dx

Or a est la dérivée de f au point x₀ ; ainsi la différentiabilité et la dérivabilité de f au point x₀ sont
synonymes ou équivalentes.

On peut écrire :

df = f ’(x₀).dx

Supposons que f est différentiable sur I. Alors en tout point x de I, on a :

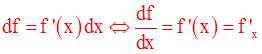
C’est la notation de Leibnitz pour les dérivées.

Remarque

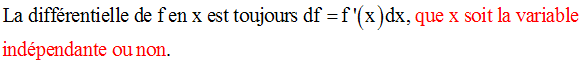
Il y a donc avantage à calculer avec les différentielles plutôt qu’avec les dérivées.

Dans les différentiations on n’a plus à se préoccuper de la variable par rapport à laquelle on différentie.

Les exemples qui suivent nous le montrent.
 

1)

Soit la fonction numérique composée :

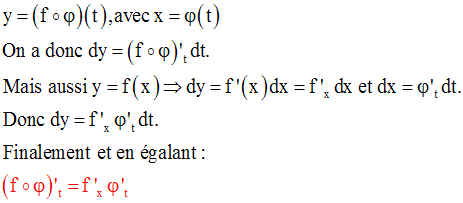
Le calcul différentiel nous a permis de retrouver facilement la dérivée d’une fonction composée.

2)

Soient u(x) et v(x) deux fonctions numériques différentiables, donc dérivables sur un intervalle réel ouvert I.
 

On a :

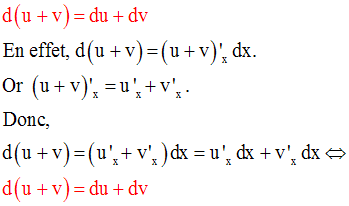
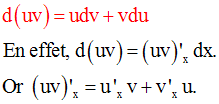
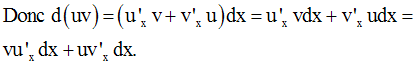
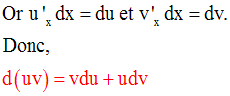
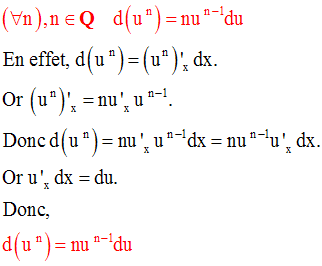
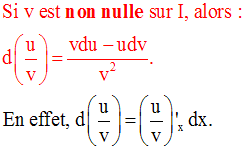
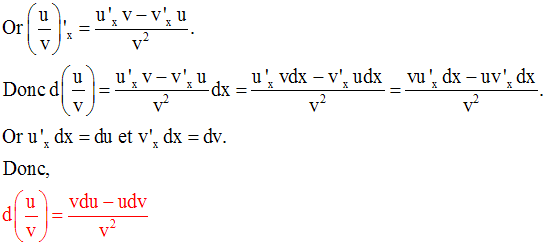
Remarque 

Les formules donnant la différentielle d’une somme et celle d’un produit s’étendent à un nombre
quelconque de fonctions numériques.

Exercice

Solution
 

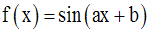
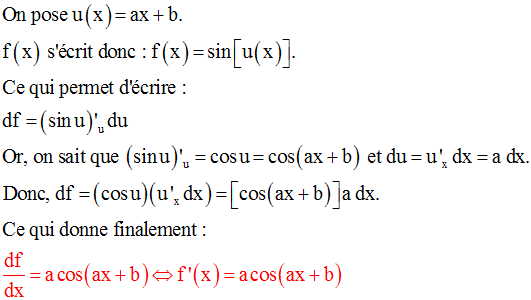
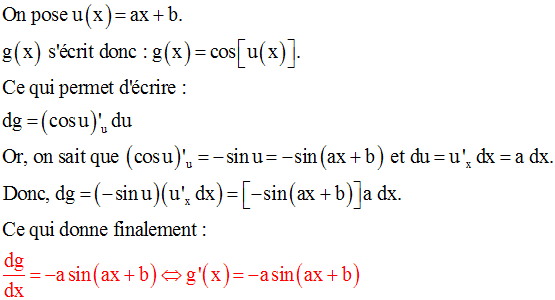
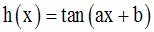
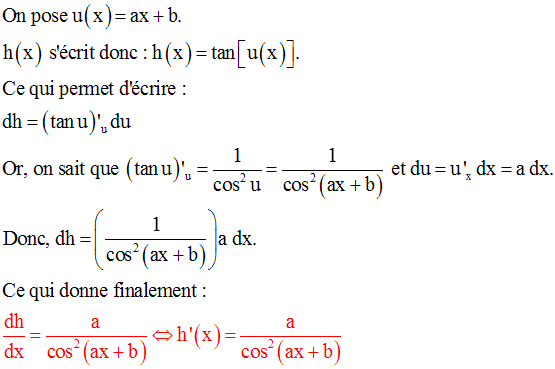
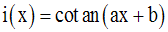
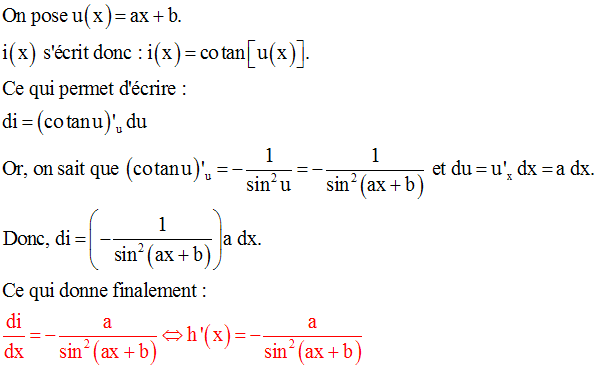
Interprétation géométrique d’une différentielle

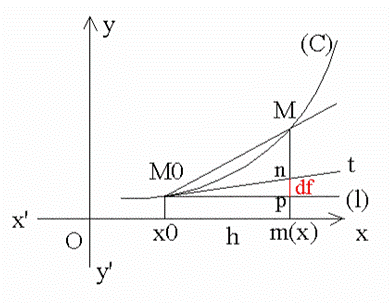
Soit f une fonction différentiable sur un intervalle réel ouvert I.

Soit, dans un repère orthonormal, (C) la courbe représentative de f.

Soit x₀ élément de I et M₀ le point de (C) d’abscisse x₀.

Prenons un réel quelconque Δx = h différent de 0 et tel que x = x₀ + h soit un élément de I.

Soit le point M de (C) dont l’abscisse est x.

Soit m le projeté orthogonal de M sur l’axe des abscisses.

De M₀ menons la tangente (M₀ t); on sait que la pente de cette tangente est égale à a.

(M₀ t) coupe (Mm) en n et la parallèle (l), menée de M₀  à l’axe des abscisses, coupe (Mm) en p.

Dans le triangle rectangle (M₀ pn),

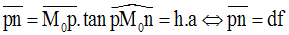
Par ailleurs on a :

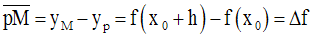
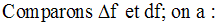
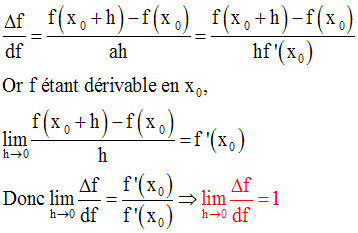
Ce résultat justifie l’approximation fréquemment utilisée en Sciences Physiques.

Si f est une fonction numérique dérivable, donc différentiable, en x₀ et si sa dérivée est non nulle
en ce point, alors :

Exemple :

Soit f la fonction numérique définie par :

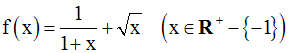
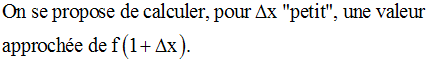
On a :

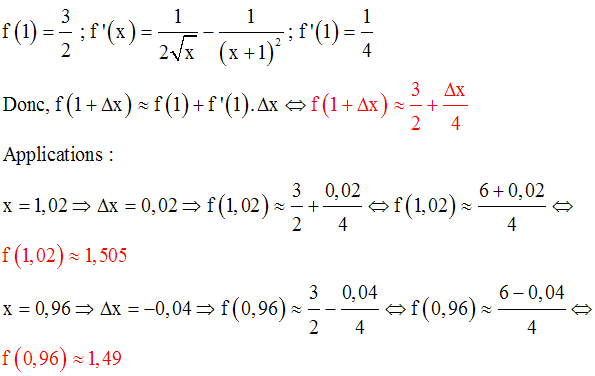
Différentielle de second ordre

Soit y = f(x) une fonction numérique deux fois dérivable, donc deux fois différentiable
sur un intervalle réel ouvert I.

On appelle différentielle seconde (ou de second ordre) de f, et on note d² f ou d² y, la différentielle
de df ou dy.

x étant la variable indépendante, on a :

Remarque

Ce résultat n’est plus valable si x n’est pas la variable indépendante.

Exercices de récapitulation, en parties résolus ou comportant des indications ou recommandations

1)

On donne le cercle trigonométrique (C) de centre O et de rayon 1.

Le point A(1) est l’origine des arcs pris sur ce cercle (Figure ci-dessous).

Soit M un point quelconque de (C).

La droite perpendiculaire à (OA) menée de M rencontre  (OA) au point P.

De A on élève la droite perpendiculaire à (OA) qui rencontre (OM) au point T.

Démontre que l’on a :

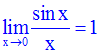
Solution

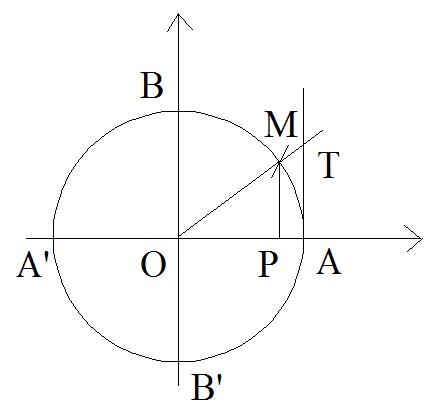
1^er cas : x > 0

Dans ce cas, on a :



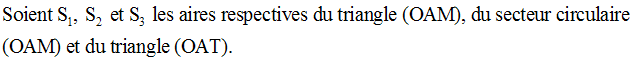
On a :

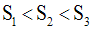
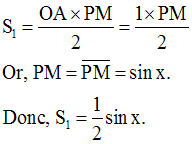
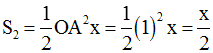
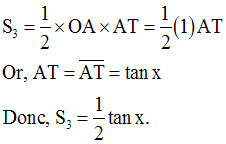
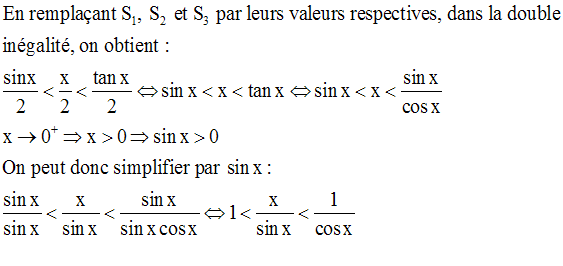
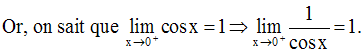
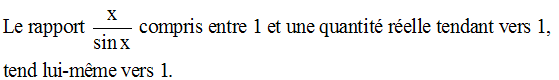
Ainsi,

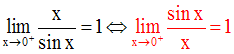
2^ème cas : x < 0

Dans ce cas, on a :


 

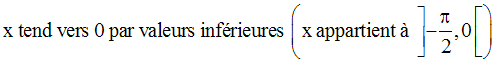
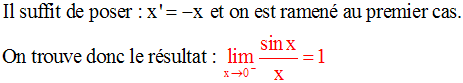
Conclusion :

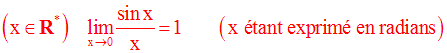
2)

Le théorème de Rolle

Soit f une fonction numérique continue sur l’intervalle réel [a,b], dérivable sur ]a,b[ et telle que f(a) = f(b).

Démontre qu’avec ces hypothèses, il existe au moins un réel c appartenant à ]a,b[ et tel que f ’(c) = 0.

Solution

On écarte d’abord le cas où f est une fonction constante sur [a,b] ; en effet, dans ce cas la dérivée de f
est constamment nulle sur [a,b] et le théorème est vérifié quel que soit c élément de [a,b].

f n’étant pas constante sur [a,b] et étant continue sur cet intervalle, Max(f) = M et Min(f) = m existent
et sont telles que l’une au moins est différente de f(a) et de f(b).

On suppose, par exemple, que M est différente de f(a) = f(b).

Il existe au moins un réel c appartenant à ]a,b[ et tel que f(c) est égale à M.

On a donc :

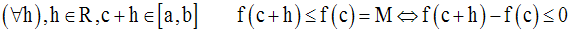
Il s’ensuit que :

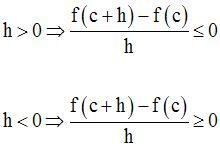
Donc, on a :

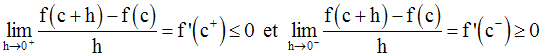
Or, f étant dérivable sur ]a,b[, est dérivable au point c appartenant à cet intervalle et on a finalement :

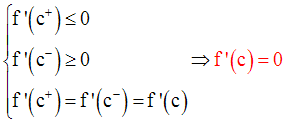
Remarque :

Géométriquement, le théorème de Rolle affirme l’existence d’au moins un point du graphe de f, (f vérifiant les conditions du théorème), où la tangente est parallèle à l’axe des abscisses.

3)

Le théorème des accroissements finis

Soit f une fonction numérique définie sur l’intervalle [a,b].

Par définition, la quantité f(b) – f(a) est appelée accroissement fini de f.

On suppose que f est continue sur [a,b] et dérivable sur ]a,b[.

Démontre qu’il existe au moins un réel c appartenant à ]a,b[ tel que :

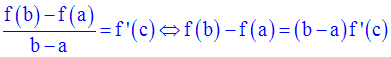
Solution

On considère la fonction numérique :

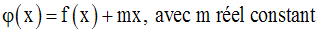
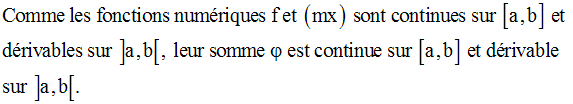
Remarque 1 :

Remarque 2 :

4)

La formule généralisée des accroissements finis

On donne deux fonctions numériques f et g, continues sur [a,b] et dérivables sur ]a,b[.

On suppose que :

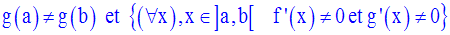
Démontre qu’il existe au moins un réel c appartenant à ]a,b[ tel que :

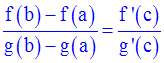
Solution

On considère la fonction numérique :

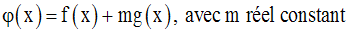
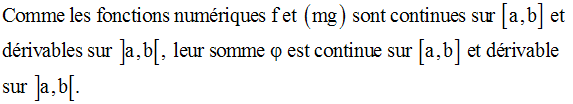
On trouve aisément :

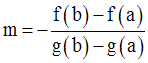
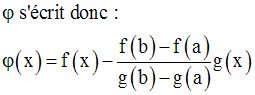
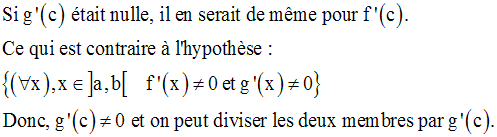
On obtient :

5)

La règle de l’Hospital

On donne deux fonctions numériques f et g, continues sur [a,b] et dérivables sur ]a,b[.

On suppose que g’ ne s’annule pas sur ]a,b[.

On demande de démontrer que l’on a :

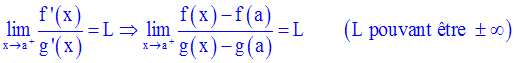
Solution

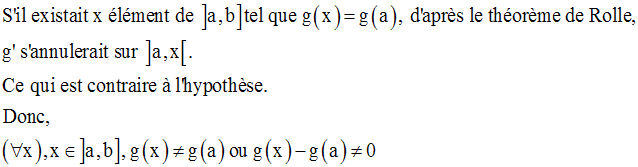
Par ailleurs, x étant un élément quelconque de ]a,b], on définit sur l’intervalle ]a,x] une fonction
numérique h comme suit :

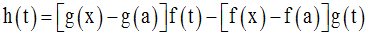
On a :

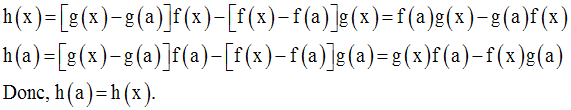
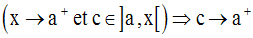
Donc,

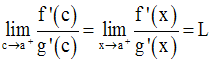
Par conséquent,

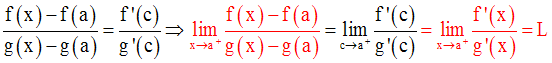
Remarque 1 :

La règle de l’Hospital s’applique également lorsque f est définie sur [a,b[ et qu’on considère la limite
lorsque x tend vers b inférieurement.

Il s’applique aussi lorsqu’on travaille sur l’ensemble :

[a,b] – {c} et qu’on considère la limite en c.

Remarque 2 :

La réciproque de la règle de l’Hospital est fausse.

Pour le vérifier, il suffit de prendre par exemple :

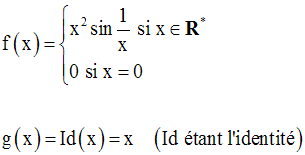
On a :

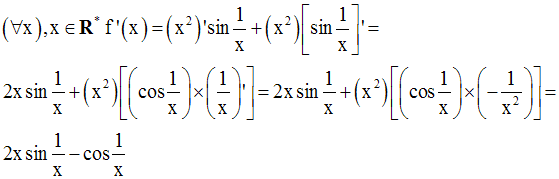
Par conséquent,

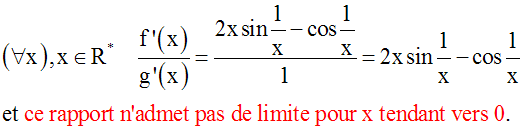
Pourtant, on a :

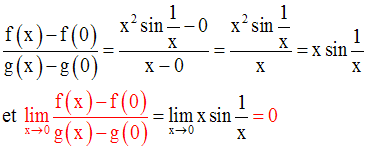
Remarque 3 :

Une autre règle de l’Hospital

6)

Détermine les fonctions dérivées des fonctions numériques f suivantes ; le cas échéant, tu préciseras
l’ensemble de dérivabilité de chacune de ces fonctions :

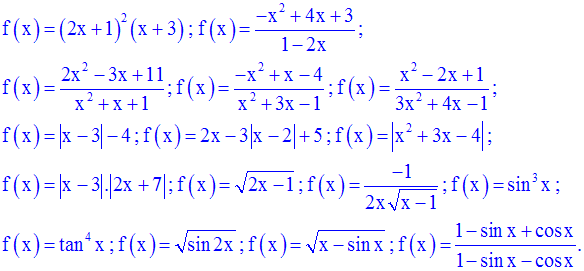
Cet exercice ne présente aucune difficulté ; cependant, il faudra faire attention au fait que,
sous certaines conditions, l’expression de la dérivée change.

7)

Si A est ce point de tangence, ses coordonnée doivent d’abord vérifier l’équation de (H),
puisque A appartient à (H).

D’où l’équation :

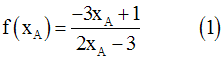
Ensuite, comme la pente de la tangente en A à (H) n’est que la valeur de la dérivée pour x égale à
l’abscisse de A, on obtient une seconde équation :

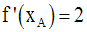
On aura donc à résoudre cette équation et on obtiendra l’abscisse de A.

En remplaçant ensuite x_A par cette valeur trouvée dans l’ équation (1), on tire l’ordonnée de A.

8)

Détermine les fonctions dérivées, jusqu’à l’ordre 5, des fonctions numériques f suivantes :

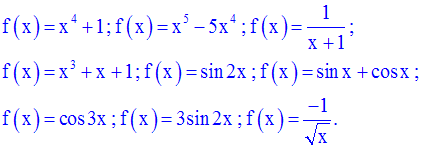
Cet exercice ne présente aucune difficulté.

9)

Solution

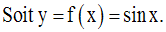
Sur cet intervalle, elle admet une dérivée f ’ égale à :

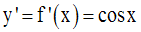
On a :

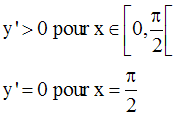
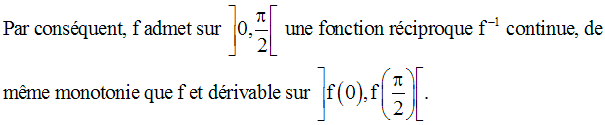
On peut facilement démontrer que cette fonction réciproque est également dérivable, à droite au point 0.

On peut donc écrire :

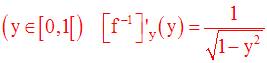
Remarque :

Conclusion

Cette conclusion nous permet donc de définir une nouvelle fonction numérique i comme suit :

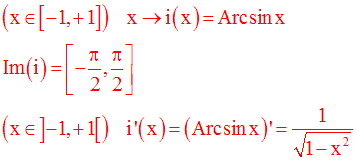
Cette nouvelle fonction numérique est appelée fonction Arc sinus.

Elle est continue, strictement croissante sur son domaine de définition.

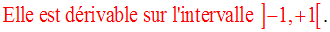
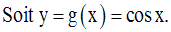
Sur cet intervalle, elle admet une dérivée g’ égale à :

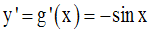
On a :

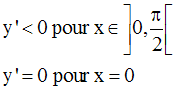
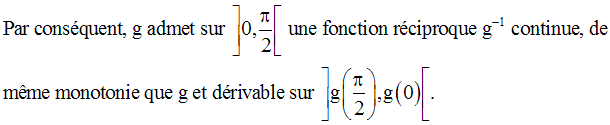
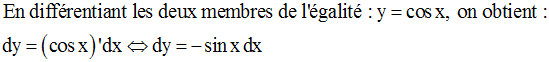
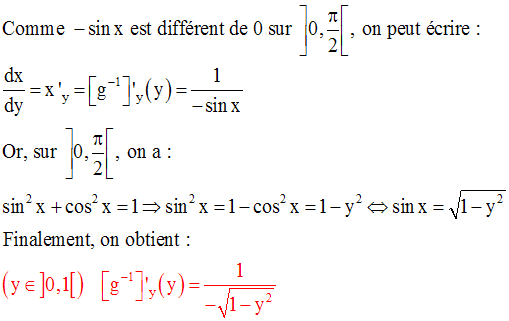
On peut facilement démontrer que cette fonction réciproque est également dérivable, à droite au point 0.

On peut donc écrire :

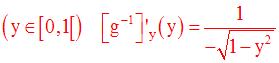
Remarque :

Conclusion

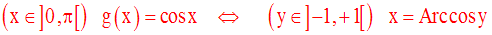
Cette conclusion nous permet donc de définir une nouvelle fonction numérique h comme suit :

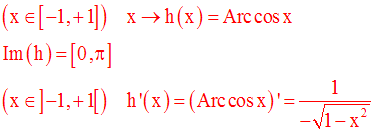
Cette nouvelle fonction numérique est appelée fonction Arc cosinus.

Elle est continue et strictement décroissante sur son domaine de définition.

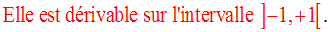
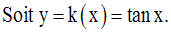
Sur cet intervalle, elle admet une dérivée k’ égale à :

On a :

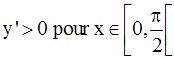
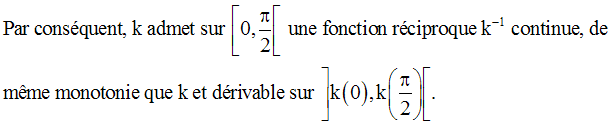
On peut facilement démontrer que cette fonction réciproque est également dérivable, à droite au point 0.

On peut donc écrire :

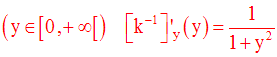
Remarque :

Conclusion

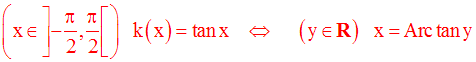
Cette conclusion nous permet donc de définir une nouvelle fonction numérique m comme suit :

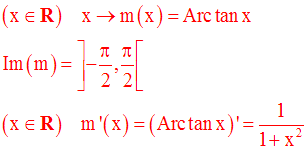
Cette nouvelle fonction numérique est appelée fonction Arc tangente.

Elle est continue, strictement croissante et dérivable sur son domaine de définition.

10)

Cet exercice ne présente aucune difficulté.

11)

Montre que la fonction dérivée d’une fonction numérique paire (resp. impaire) est une fonction
numérique impaire (resp. paire).

Cet exercice ne présente aucune difficulté.

12)

Montre que la fonction dérivée d’une fonction numérique périodique est une fonction numérique
périodique de même période.

Cet exercice ne présente aucune difficulté.

13)

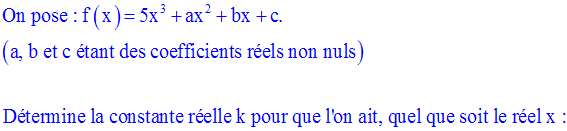
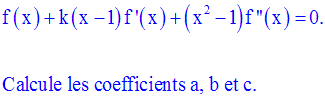
On calcule d’abord les expressions des deux premières dérivées.

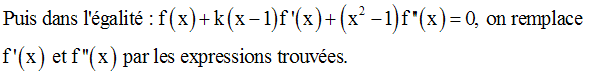
Ensuite, on développe le premier membre de l’égalité ; on doit obtenir un polynôme du troisième degré en x.

Pour que ce polynôme soit identiquement nul (c’est-à-dire, nul pour tout réel x), il faut et il suffit que
tous ces coefficients soient nuls.

On doit trouver :

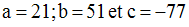
14)

Solution

a-

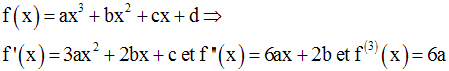
On suppose que l’on a, pour h réel quelconque :

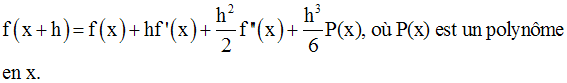
On doit démontrer que P(x) n’est autre que la dérivée troisième de f, c’est-à-dire, 6a.

On a :

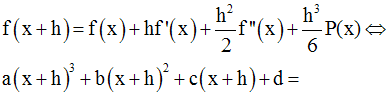
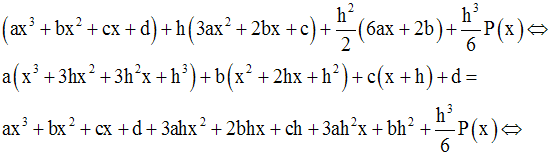
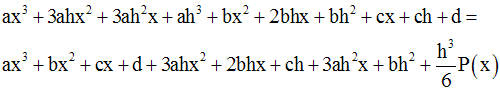
En simplifiant, on obtient :

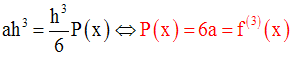
Conclusion :

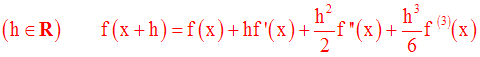
b-

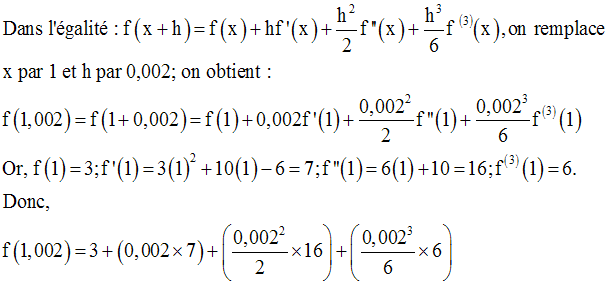
15)

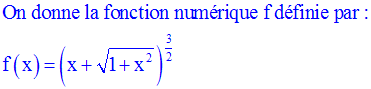
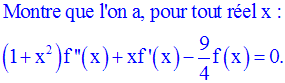
Cet exercice ne présente aucune difficulté.




16)

Cet exercice ne présente aucune difficulté.




17)

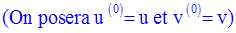
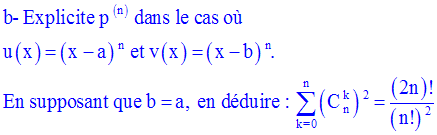
Solution

a-

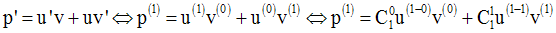
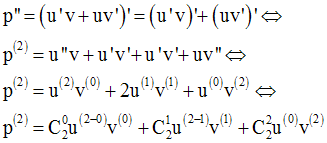
La formule est donc vérifiée jusqu’au rang 2.

On suppose qu’elle l’est jusqu’au rang (n – 1) et on démontre qu’elle l’est pour n.

On a donc par hypothèse :

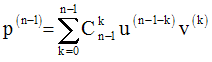
Dérivons cette dernière fonction :

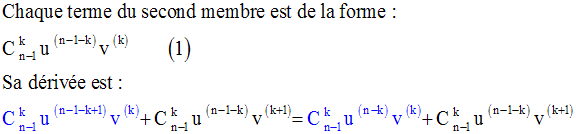
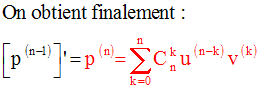
C’est la formule de Leibnitz.

b-

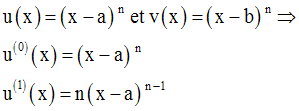
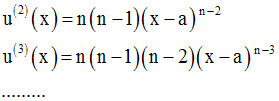
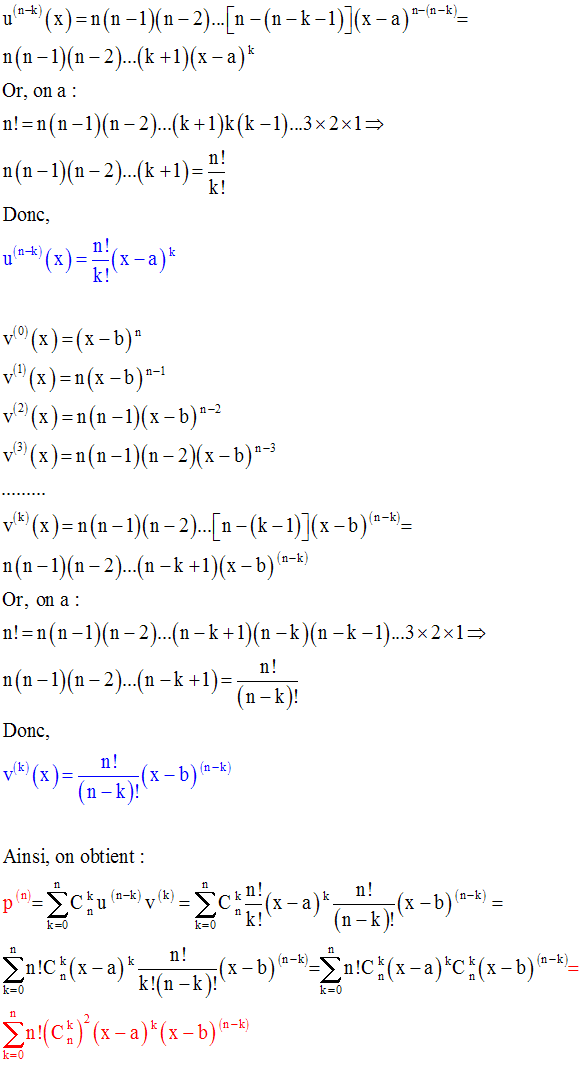
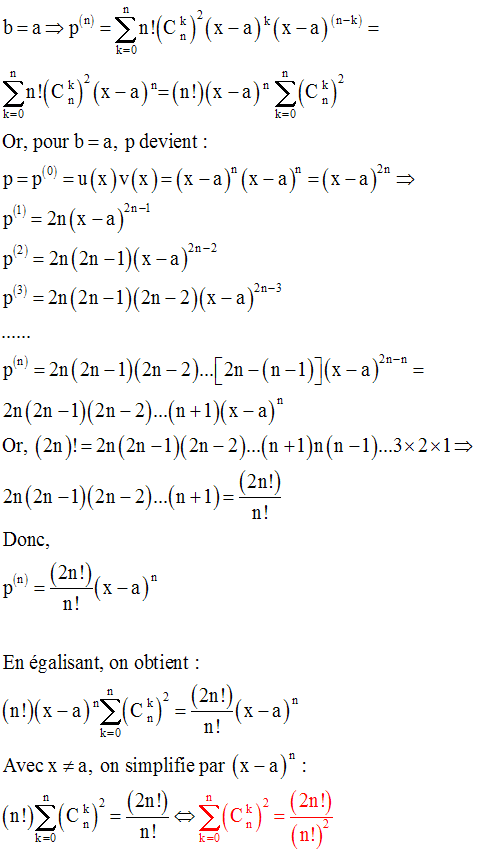
Deux remarques importantes :

1-

Il ne faut pas confondre la puissance n d’une fonction u qui s’écrit : uⁿ  et la dérivée d’ordre n de u
qui s’écrit u⁽ⁿ⁾.

2-

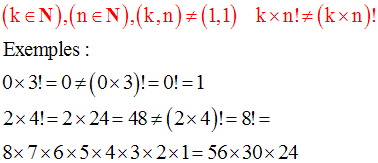
18)

Solution
 

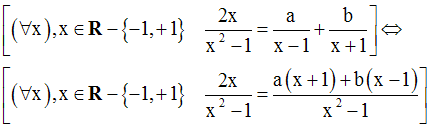
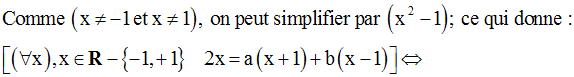
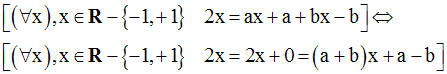
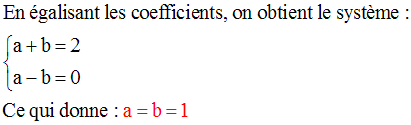
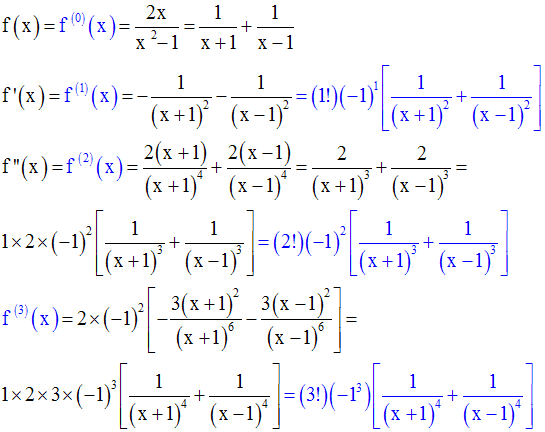
L’égalité est vraie jusqu’au rang 3.
 

On suppose qu’elle l’est pour le rang (n – 1) ; donc on a :

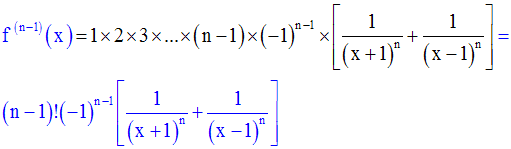
On démontre qu’elle reste vraie pour le rang n.
 

Pour cela, il suffit de dériver cette dernière fonction ; on a :

 

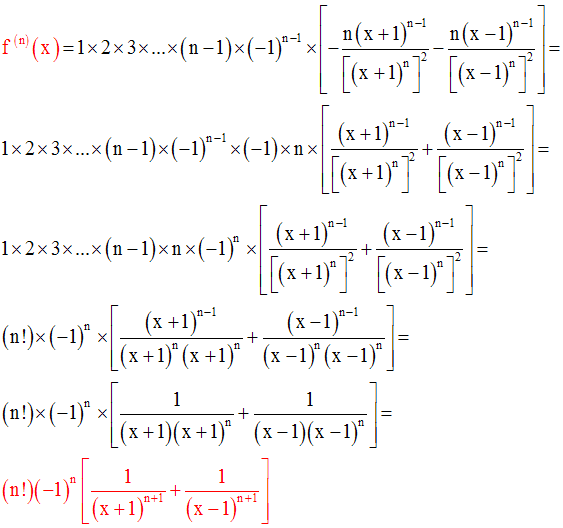
19)

Cet exercice ne présente aucune difficulté. Cependant, il faudra faire attention à l’expression
de la valeur absolue selon les valeurs que prendra x.

20)

Cet exercice ne présente aucune difficulté.




21)

Etudie les variations et construire les courbes représentatives (repère orthonormal) des
fonctions numériques suivantes :

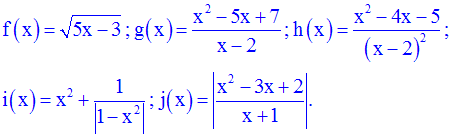
Cet exercice ne présente aucune difficulté. Cependant, pour j(x), il faudra faire attention à l’expression
de la valeur absolue selon l’ensemble des réels que x parcourra.




22)

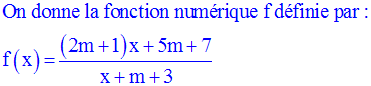
Cet exercice ne présente aucune difficulté.




23)

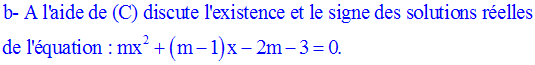
Cet exercice ne présente aucune difficulté.




24)

Cet exercice ne présente aucune difficulté.





25)

Cet exercice ne présente aucune difficulté. Cependant, il faudra faire attention à l’expression de la
valeur absolue selon les valeurs que prendra x.

Problèmes non résolus

retour au sommaire