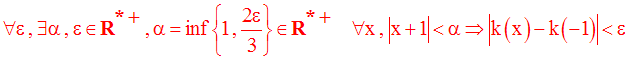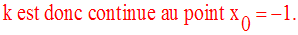1- Préalables
1-1 Rappel des propriétés de la valeur absolue d’un réel
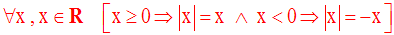
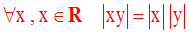
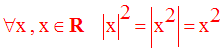
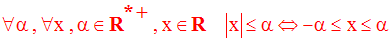



1-2 Encadrement d’un réel
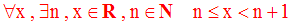
1-3 Intervalle réel centré
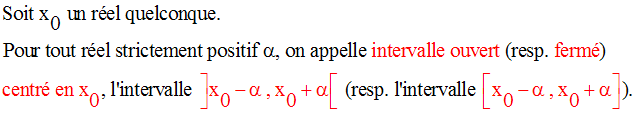
1-4 Signification de la phrase « x tend vers a »
Soit a un réel quelconque.
On dira que la variable réelle x tend vers a si et seulement si :
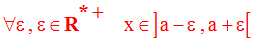
Dans ce cas on écrira :
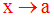
On dira que la variable réelle x tend vers a par valeurs inférieures ou négativement si et seulement si :
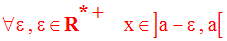
Dans ce cas on écrira :
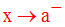
On dira que la variable réelle x tend vers a par valeurs supérieures ou positivement si et seulement si :
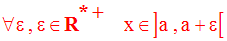
Dans ce cas on écrira :
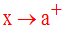
1-5 Négation d’une assertion
On donne l’assertion suivante :
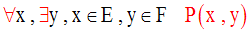
P est une propriété vérifiée par les éléments x et y.
La négation de cette assertion est l’assertion :
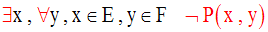
On observe bien la
nature et la place des quantificateurs universel et existentiel dans ces
deux assertions.
On observe également que dans la négation, on a exprimé la négation de la
propriété P.
On donne une seconde assertion :
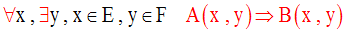
A, B sont des propriétés vérifiées par les éléments x et y.
La négation de cette assertion est l’assertion :
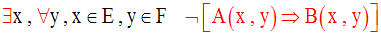
Or, on a vu en Logique
Formelle (voir la page intitulée « Notions élémentaires de Logique
Formelle),
que l’on a l’équivalence logique suivante :
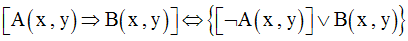
Donc, on a :
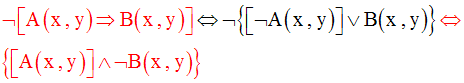
Ainsi, on obtient :
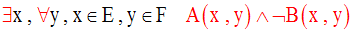
1-6 Borne inférieure d’un sous ensemble de R
Soit un sous ensemble A minoré quelconque de R.
On rappelle que le plus grand des minorants de A est appelé borne inférieure de A et est noté :
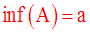
Exemples :
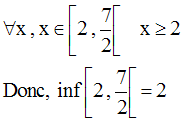
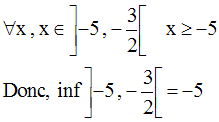
Remarque :
inf(A) n’appartient pas généralement à A ; c’est le cas dans le deuxième exemple.
2- Continuité d’une fonction numérique en un point
2-1 Continuité à droite

Avec les quantificateurs, on écrira :
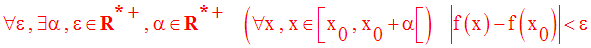
Cette définition peut également s’écrire :
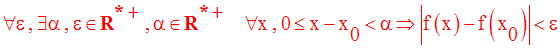
2-2 Continuité à gauche

Avec les quantificateurs, on écrira :

Cette définition peut également s’écrire :
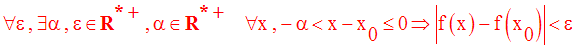
2-3 Continuité en un point

Ceci se traduit par :
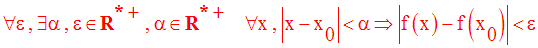
C’est cette
écriture que l’on doit utiliser pour démontrer qu’une fonction numérique
définie en un point
est continue en ce point.
3- Discontinuité d’une fonction numérique en un point
Une fonction numérique f définie en un point et n’étant pas continue en ce point sera dite discontinue en ce point.
L’écriture permettant
de démontrer la discontinuité d’une fonction numérique en un point est
la négation de celle écrite
plus haut pour la démonstration de la continuité en un point.
On obtient :
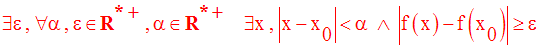
C’est cette
écriture que l’on doit utiliser pour démontrer qu’une fonction numérique
définie en un point
est discontinue en ce point.
4- Continuité d’une fonction numérique sur un intervalle réel
Soient a, b deux réels finis quelconques et supposons que a est strictement inférieur à b.
4-1 Continuité d’une fonction numérique f sur [a , b]
Soit f une fonction numérique définie sur [a , b], c’est-à-dire définie en tout point appartenant à [a , b].
On dit que f est continue sur [a , b] si et seulement si f est :
- continue en tout point x appartenant à ]a , b[
- continue à gauche en b
- continue à droite en a
4-2 Continuité d’une fonction numérique f sur I, sachant que I est un des intervalles réels suivants :
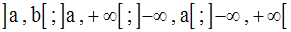
f étant définie sur I, on dit qu’elle est continue sur I si et seulement si continue en tout point appartenant à I.
4-3 Continuité d’une fonction numérique f sur un des intervalles réels suivants :
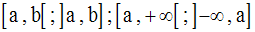
f étant définie sur chacun de ces intervalles, on dit que f est continue sur :



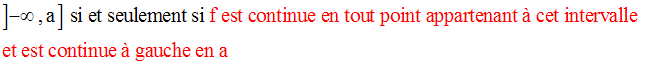
5- Applications
Application 1
On a vu plus haut que l’on a la propriété :
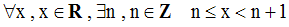
n sera appelé la partie entière de x qu’on désignera par E(x).
Exemples :
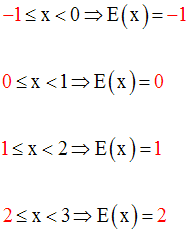
Soit la fonction numérique f définie comme suit :
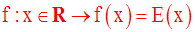
f sera appelée fonction partie entière.
Il s’agit de démontrer que f est continue à droite
en tout point n, n étant un entier relatif.
Démonstration
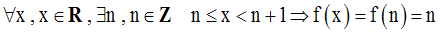
Ceci se traduit par :
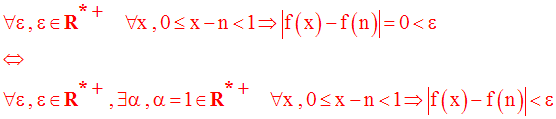
Par conséquent, f est continue à droite en n.
Par ailleurs, on démontre également que f est discontinue à gauche en n.
Démonstration
Il s’agit de démontrer que l’on a :
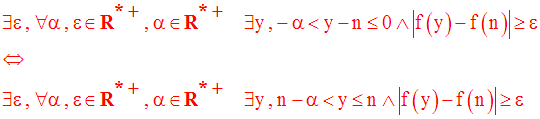
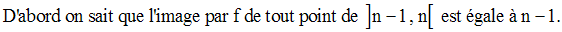
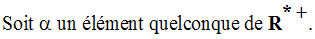
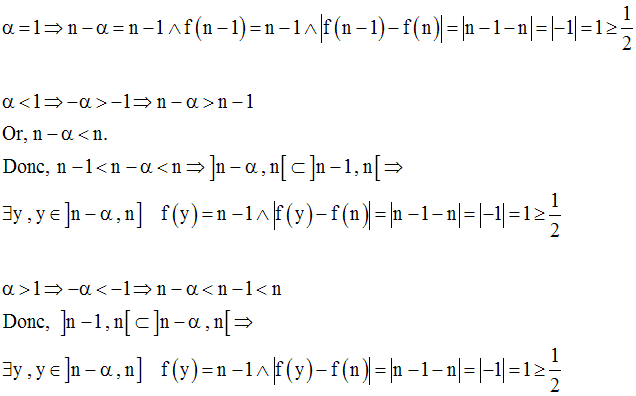
Conclusion
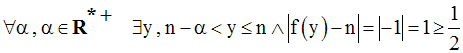
Ce qui s’écrit également :

f est donc discontinue à gauche au point n.
f étant continue à droite en n et discontinue à gauche en n est discontinue en n.
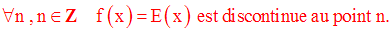
Application 2
Soit la fonction numérique f définie par :
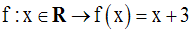
Démontre que f est continue en tout point appartenant à son domaine de définition.
Solution
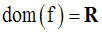
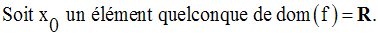
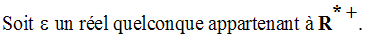
On cherche donc à avoir :
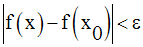
On a :
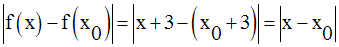
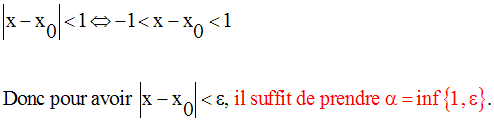
Ainsi, on a :
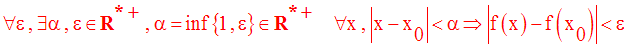

Application 3
Soit la fonction numérique g définie par :
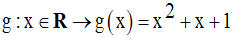

Solution
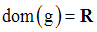
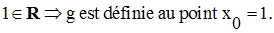
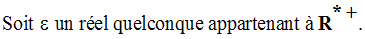
On cherche donc à avoir :
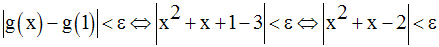
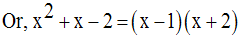
Donc,
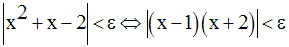
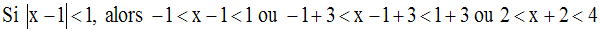

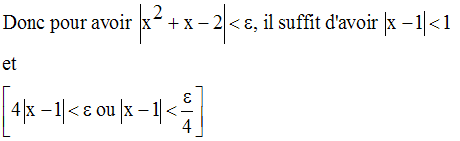

On a donc :
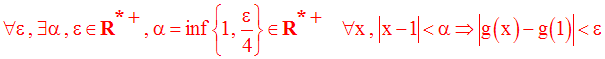

Application 4
Soit la fonction numérique h définie par :

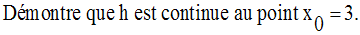
Solution
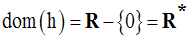
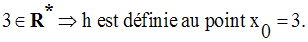
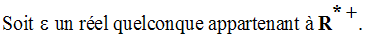
On cherche donc à avoir :
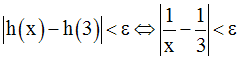
On sait que :
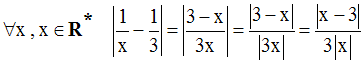
Donc,
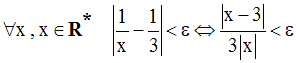
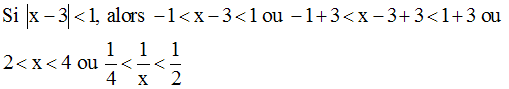
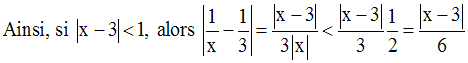
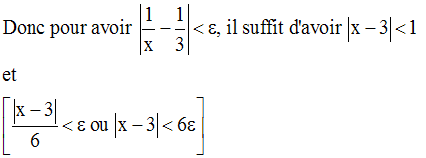

On a donc :
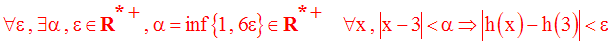

Application 5
Soit la fonction numérique i définie par :
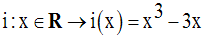
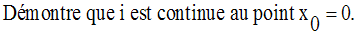
Solution
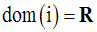
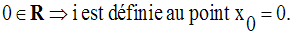
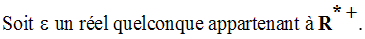
On cherche donc à avoir :
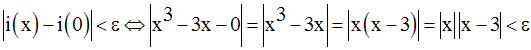
On sait que :
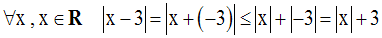
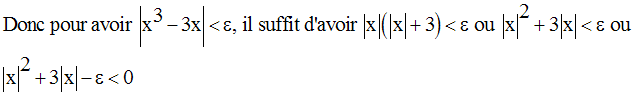
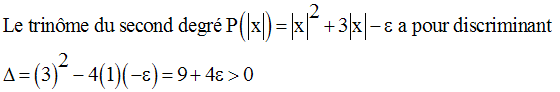
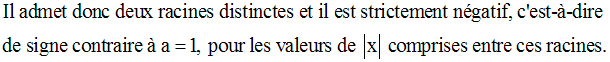
Les racines sont :
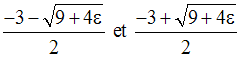
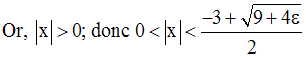
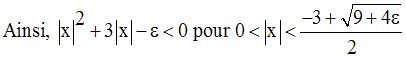

On a donc :
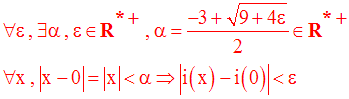

Application 6
Soit la fonction numérique j définie par :
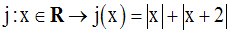
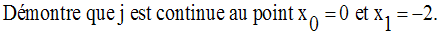
Solution
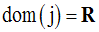

j portant sur des valeurs absolues, il faut d’abord trouver ses différentes expressions dans les intervalles suivantes :
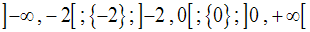
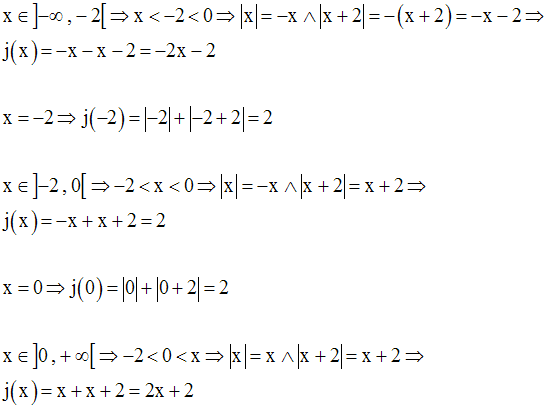
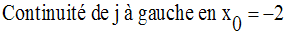
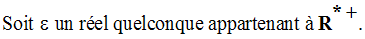
On cherche donc à avoir :
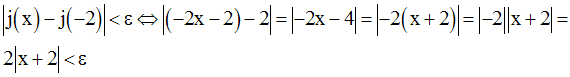
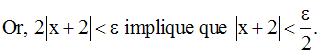
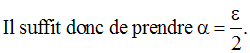
On a donc :
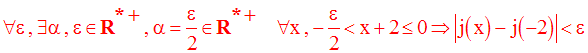
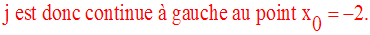

L’intervalle d’étude est donc :
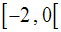
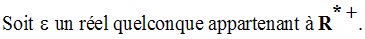
On cherche donc à avoir :
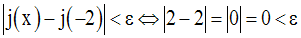
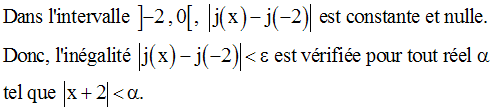
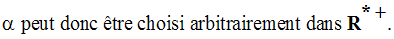
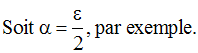
On a donc bien :
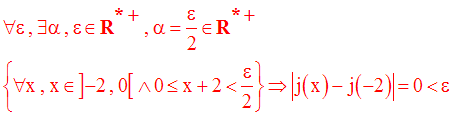
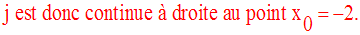
Conclusion

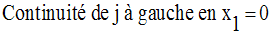
L’intervalle d’étude est donc :
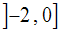
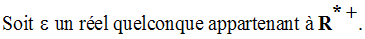
On cherche donc à avoir :
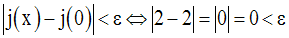
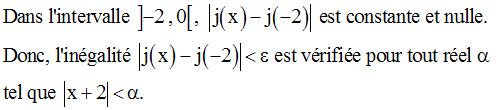
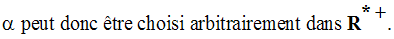
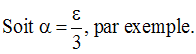
On a donc bien :
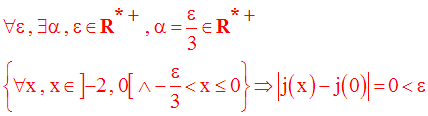
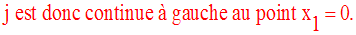
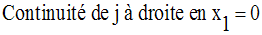
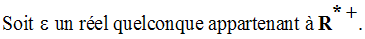
On cherche donc à avoir :
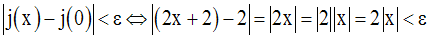
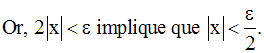
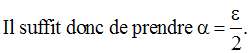
On a :
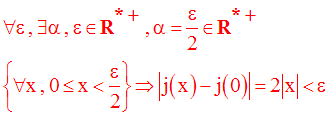
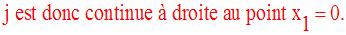
Conclusion
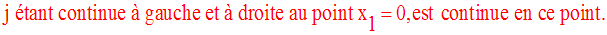
Application 7
Soit la fonction numérique k définie par :
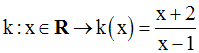
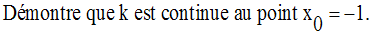
Solution
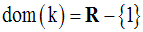
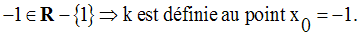
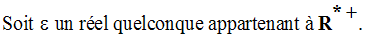
On cherche donc à avoir :
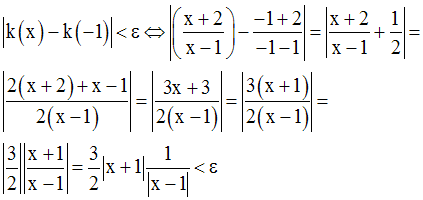
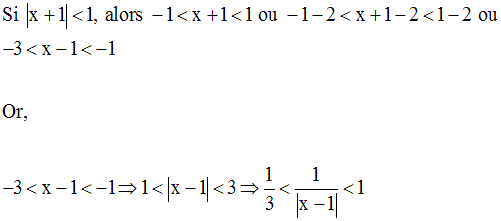
Pour avoir :
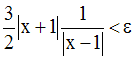
Il suffit d’avoir :
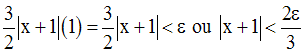
Ainsi, on a :
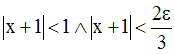

On a ainsi :