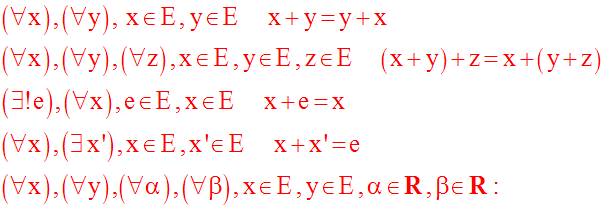
Définitions
Soit E un ensemble non vide.
E sera dit
R-espace vectoriel
si et seulement si E est muni d’une
addition, notée (+), partout
définie dans E et d’une application de E × R dans R notée (.),
cette addition et cette application vérifiant les propriétés suivantes :
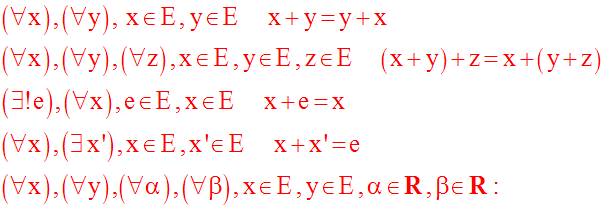
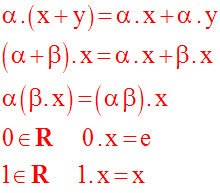
Les éléments x du R-espace vectoriel E seront nommés vecteurs et seront notés :
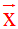
L’élément unique
e est dit élément neutre
pour l’adition (+).
Il est nommé vecteur nul et noté :
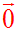
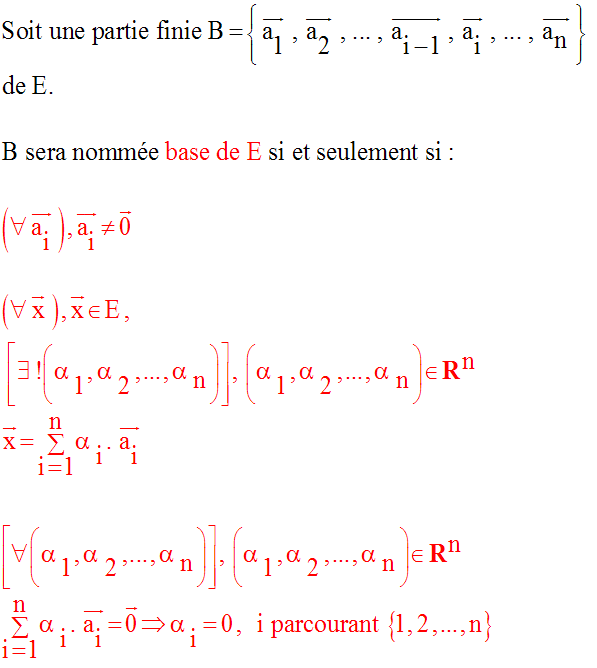
Si E possède une base B et si
card (B) = n, alors on dira que
le R-espace vectoriel E
est de dimension n.
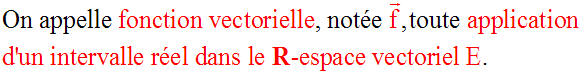
Pour la suite on considérera un R-espace vectoriel E de dimension 3.
Sa base sera notée :
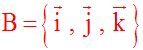
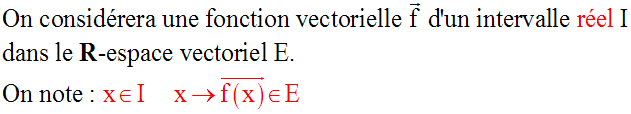

On a vu en classes de première
et de seconde les objets mathématiques appelés
vecteurs de l’espace physique à trois dimensions.
Appelons Ω l’ensemble de ces vecteurs.
Exercice
Montre que Ω est un R-espace vectoriel.
Mouvement d’un point – Trajectoire
R sera considéré
comme l’espace des temps dont tout élément réel
sera noté t ; donc
l’intervalle de définition I de l’application f est une partie de cet espace des
temps.
L’espace (Ω , O) est rapporté à un repère orthonormal (R), la base étant :
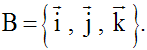
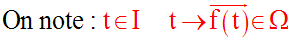

Soit dans l’espace du repère (R) le point M tel que :
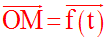

Remarque importante
La notion de mouvement est
relative ; en effet, un mobile peut être
simultanément au repos par rapport
à un repère (R) et en mouvement par
rapport à un autre repère (R’).
Par exemple, un voyageur
assis dans une voiture de train est
au repos par rapport au train,
donc aussi par rapport à tout repère fixe pris dans le
train.
Mais
simultanément, ce même voyageur est en mouvement
par rapport à tout repère
fixe dont l’origine est le centre de gravité de la gare de destination.
La
trajectoire du mobile M par rapport au repère (R)
est l’ensemble des points liés à ce
repère avec lesquels le point mobile coïncide
successivement.
La trajectoire est donc une courbe fixe par rapport au repère (R).
Détermination du mouvement

On écrit :
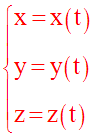
Par élimination de t, on peut obtenir l’équation cartésienne de la trajectoire de M.
dans tout ce qui suit, on supposera la
fonction vectorielle déterminant
le mouvement deux fois dérivable, c’est-à-dire que les fonctions numériques
x(t), y(t) et z(t) admettent des dérivées première et seconde sur l’intervalle
réel I
par ailleurs les résultats et
propriétés obtenus dans le repère orthonormal de l’espace
sont également vrais dans tout repère orthonormal du plan
Le mouvement peut être également déterminé par la fonction numérique φ, telle que u = φ(t).
Ainsi, à chaque valeur du temps t est associée une valeur du paramètre u = φ(t), qui à son tour détermine la position de M puisque l’on a :
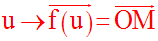
La relation u = φ(t) est appelée loi horaire du mouvement.
La courbe représentative de
cette fonction numérique u = φ(t) est nommée
diagramme
du mouvement.
Remarque importante
On ne doit pas
confondre le
diagramme du mouvement et la trajectoire
du point mobile.
Ce sont deux objets différents.
Exercice

Vecteur-vitesse et vecteur-accélération

Ainsi, le vecteur vitesse du point mobile M est, à tout instant t, égal à :
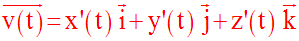
Souvent on note également :
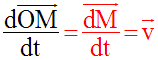
Le repère étant orthonormal, on a :
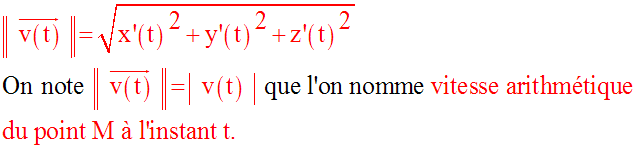
Remarque très importante
Si le mouvement de M est donné par la trajectoire, telle que :
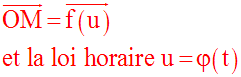
alors on se trouve dans le cas d’une fonction composée :
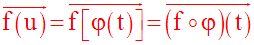
et le vecteur-vitesse a pour composantes scalaires ou coordonnées :
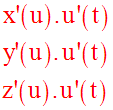
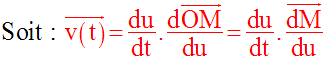

Ainsi, le vecteur accélération du point mobile M est, à tout instant t, égal à :
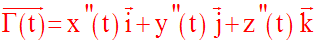
Souvent on note également :
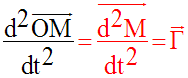

Remarque importante
Supposons le mouvement donné par la trajectoire, telle que :
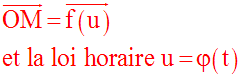
Alors le vecteur-accélération a
pour coordonnées ou composantes scalaires les dérivées
des coordonnées du vecteur-vitesse.
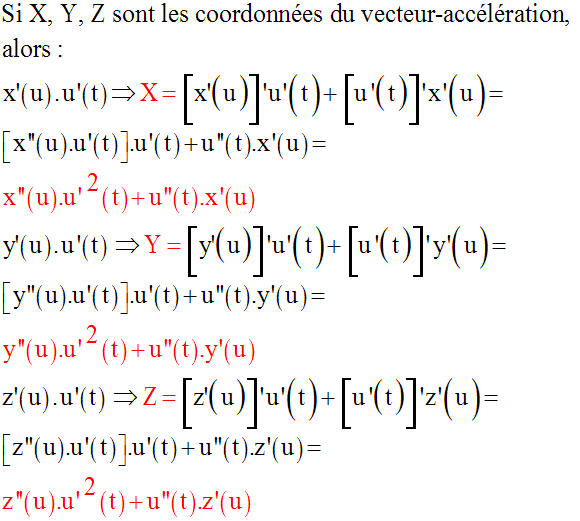
Il s’ensuit que :
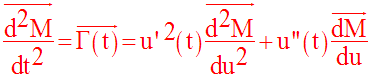
Abscisse curviligne – vitesse arithmétique – distance parcourue
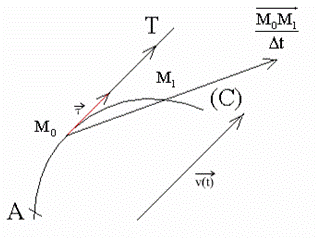
Si la trajectoire est une courbe
(C) connue, on peut choisir sur (C) un
point origine A et un
sens.
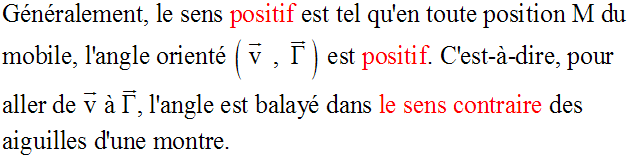


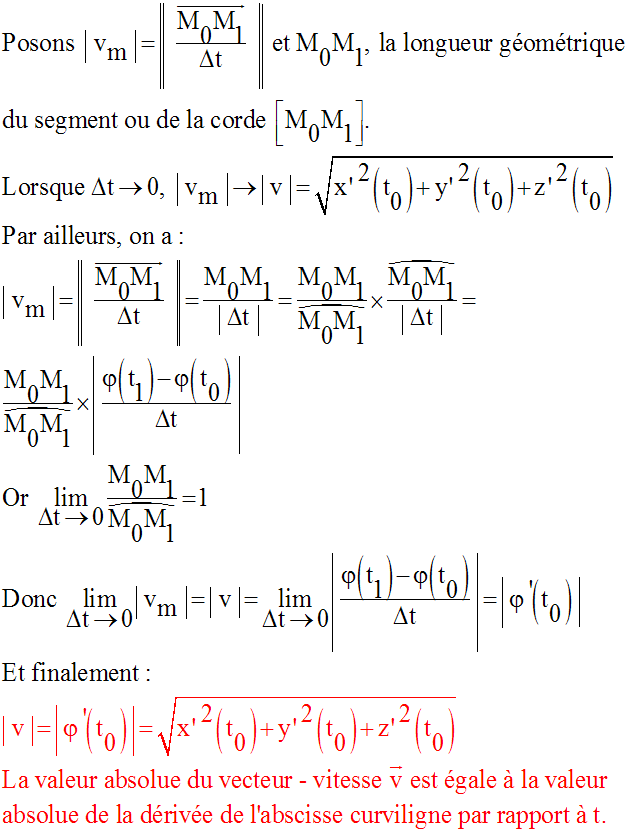
Orientons
le support de la vitesse au point M0 , c’est-à-dire la tangente à (C)
au point M0 , selon le sens du mouvement.

A tout instant, le vecteur – vitesse est porté par la tangente à la trajectoire et,
si cette
tangente est orientée dans le sens du mouvement (ou encore dans le sens pris
sur la
courbe), alors la mesure algébrique du vecteur – vitesse est la
dérivée de l’abscisse
curviligne par rapport au temps t.
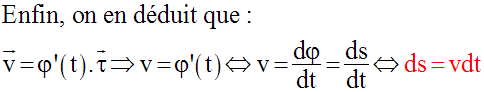
On pose D la distance parcourue par le mobile M sur la trajectoire (C).
On a donc :
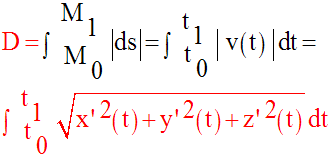
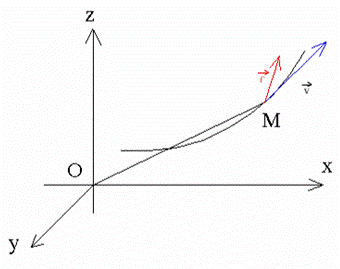
Produit scalaire – mouvement accéléré et mouvement retardé

Représentons, dans le repère, la trajectoire (C) du point mobile M.

Or, on a :
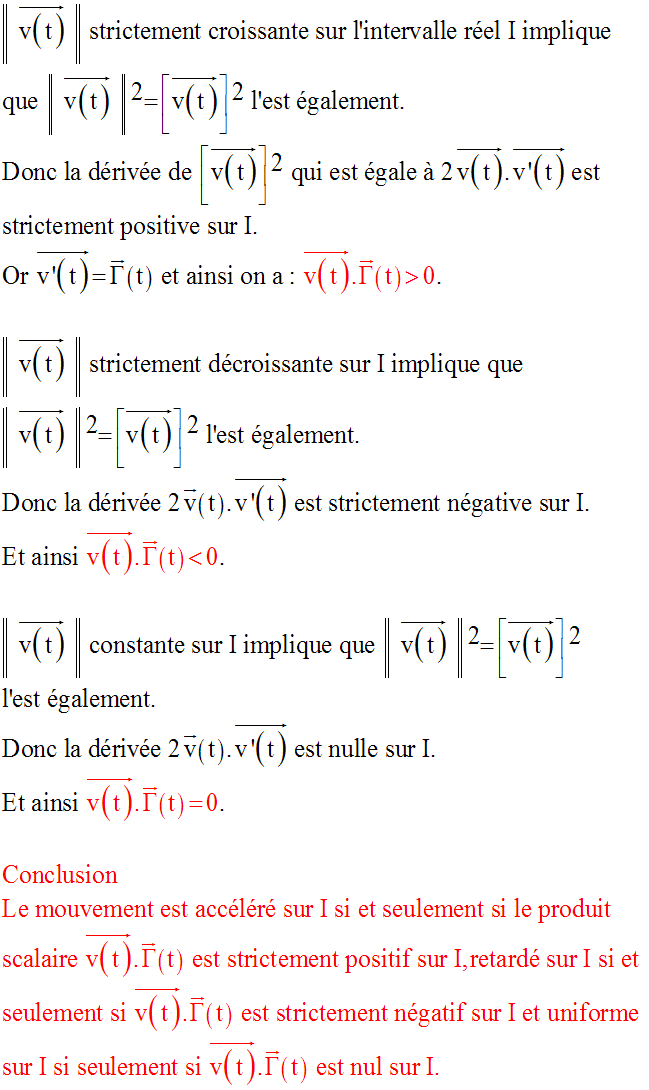
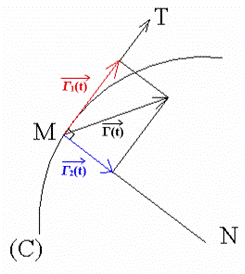
L’étude qui précède introduisant le produit scalaire :
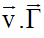
conduit à considérer
la projection orthogonale du vecteur-accélération
sur le support
de la vitesse.
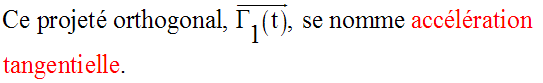

Fonction primitive d’une fonction vectorielle



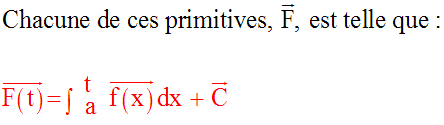
Exercices
I-

Solution
a)

Finalement, on obtient :
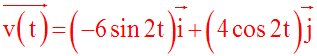
b)
On sait que :

Finalement, on obtient :
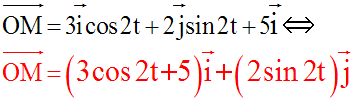
Soit la fonction cos 2t.
Soit T un réel tel que :
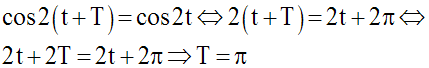
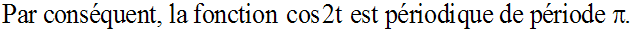
Par ailleurs, on a :
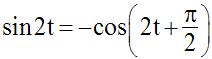
Or, pour T’ réel, on a :
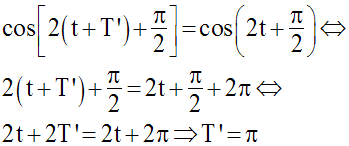
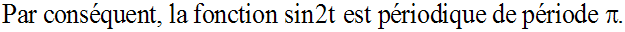

c)
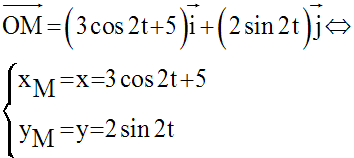
En éliminant t, on obtient l’équation cartésienne de la trajectoire de M :
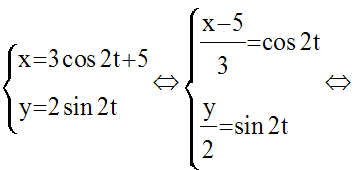
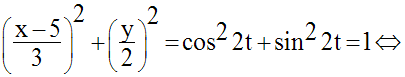
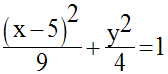
Par translation du repère de vecteur :
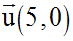
On obtient :
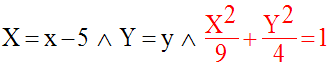
La trajectoire de M
est donc une ellipse de centre W(5 , 0), de grand axe, l’axe des
abscisses, de demi-longueur 3 et de petit axe, la droite d’équation x = 5, de
demi-
longueur 2.
II-

Solution
Soit u.a l’unité de mesure des longueurs dans le repère.
Soit d cette distance ; on a :
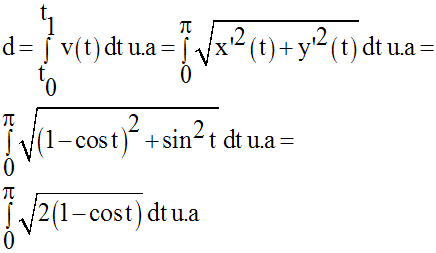
Or, on sait que :
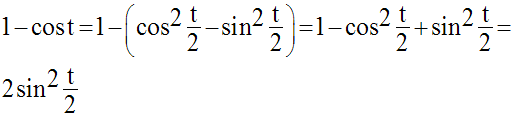
Donc,
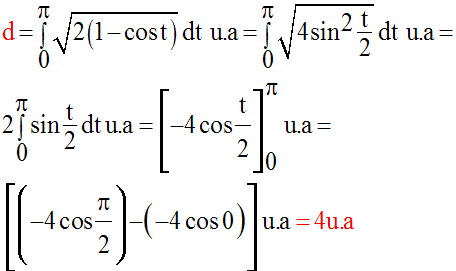
III-

Je te laisse résoudre cet exercice.
IV-

Solution
a-
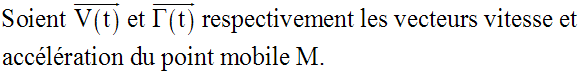
On sait que :
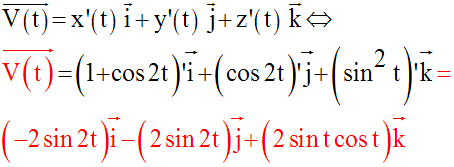
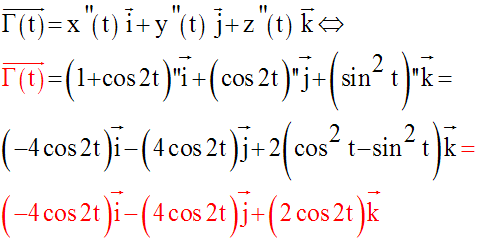
1er cas : t nul
On a :
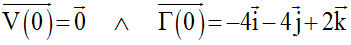
Leurs composantes scalaires sont telles que :
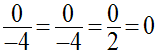
2ème cas : t différent de 0
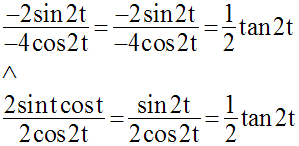
Donc,
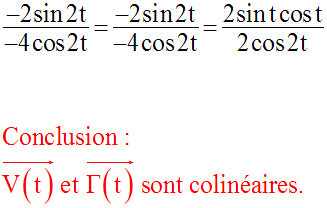
b-
On a :
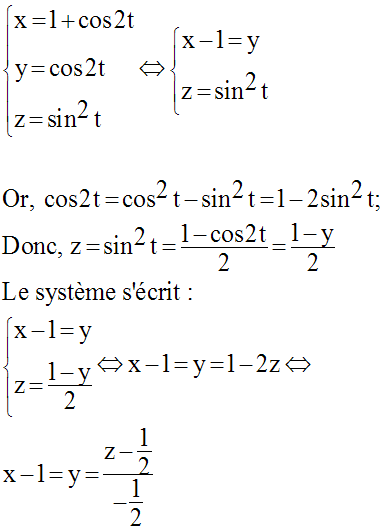
La trajectoire de M est donc la droite d’équation :
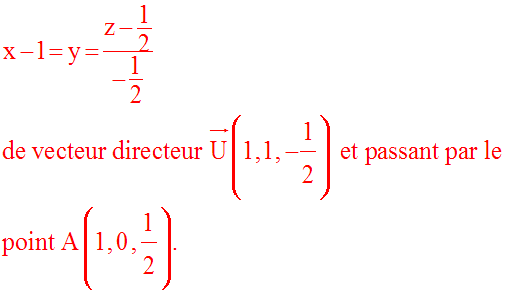
La trajectoire étant une ligne droite, les vecteurs vitesse et accélération sont colinéaires.
De plus, on remarque que :
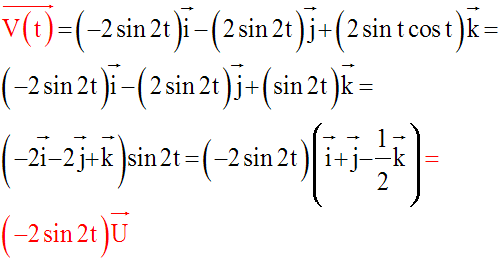
Cette relation vectorielle nous
permet de connaître le sens du mouvement. En
effet,
le sens du vecteur-vitesse est celui du vecteur
directeur de la trajectoire pour les valeurs
de t rendant la quantité (sin2t) strictement négative ;
il est contraire à celui du vecteur
directeur pour les valeurs de t rendant (sin2t) strictement positive.
c-
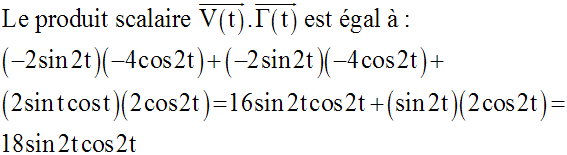
L’étude des signes de (sin 2t) et de ce produit scalaire dans les intervalles suivants :
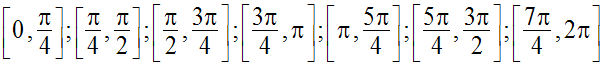
permettra de connaître le sens du mouvement ainsi que sa nature.
Soient A, B, C, D et E les positions de M respectivement aux instants suivants :
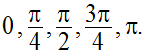
Leurs coordonnées sont :
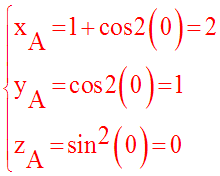
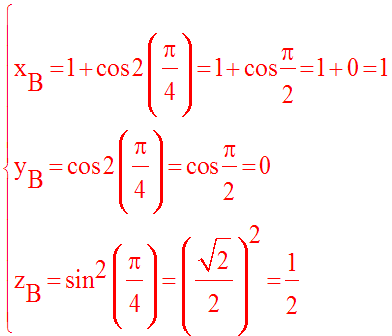
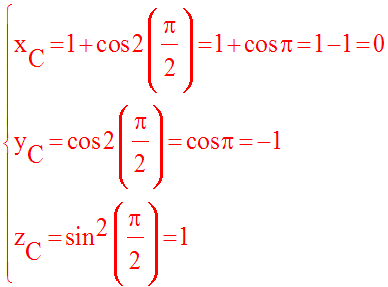
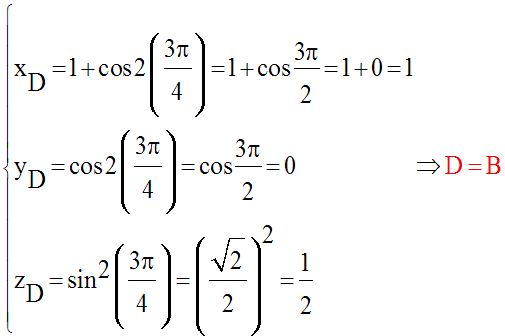
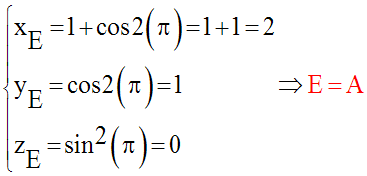
Ainsi, aux instants suivants :
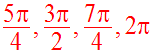
M visitera à nouveau les points B, C, B et A.

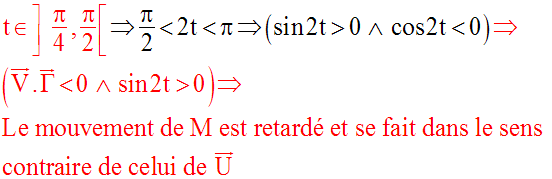
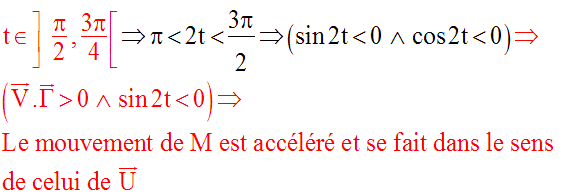
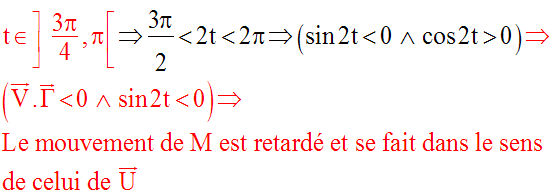
A titre d’exercice, je te laisse terminer cet exercice.
V-

Solution
En posant :
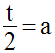
le système devient :
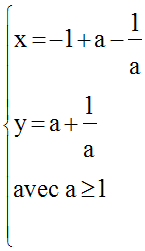
Ce qui donne :
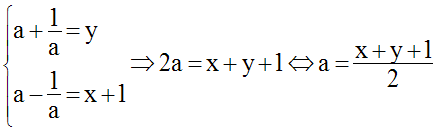
En remplaçant dans la première équation, a par son égale, on obtient :
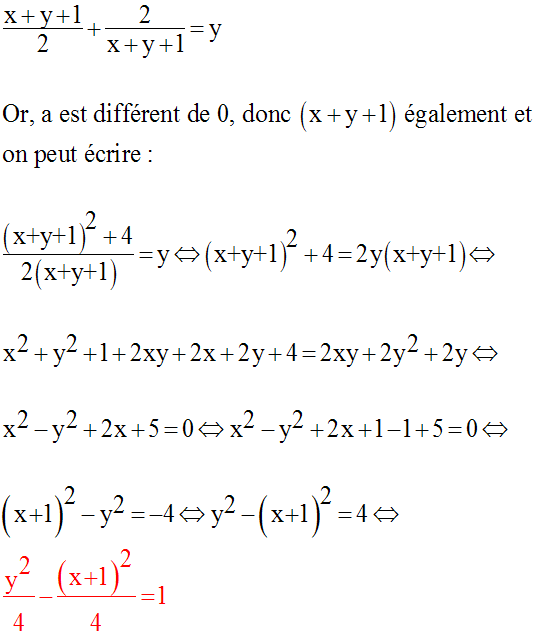
La trajectoire (C) est donc une hyperbole.
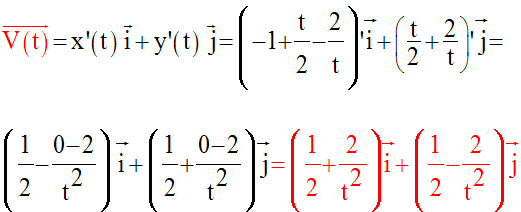
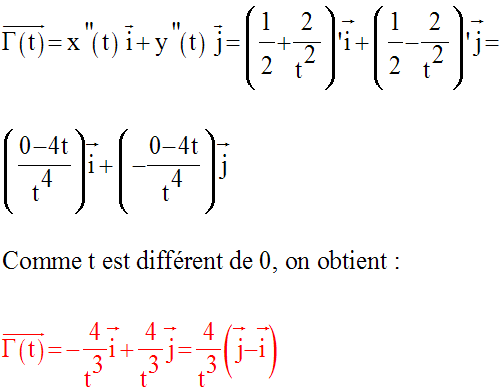
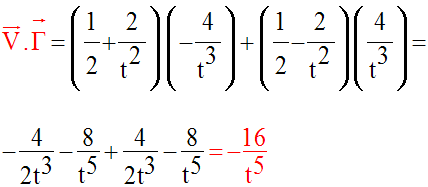
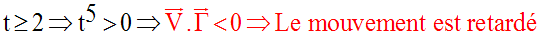
VI-

Je te laisse résoudre cet exercice.
VII-
Etude d’un mouvement particulier

On a :
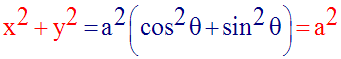
La trajectoire de M est donc le cercle de centre l’origine du repère et de rayon a.
On dit que le mouvement est circulaire.
Vecteur-vitesse

Cas particulier du mouvement circulaire uniforme

La loi horaire qui lui correspond est donc :
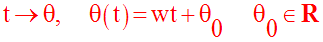
On peut facilement démontrer que ce mouvement est périodique de période T tel que :
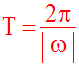
Vecteur-accélération
Pour l’obtenir, il faut dériver, par rapport à t, les composantes scalaires du vecteur-vitesse.
On a :
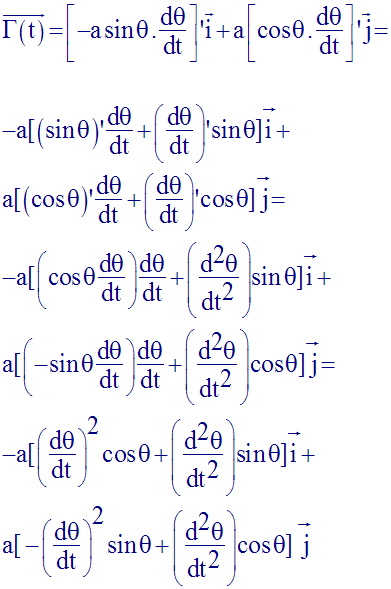
Ce qui donne en regroupant :

Finalement, le vecteur-accélération s’écrit :
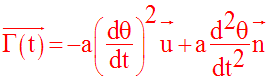
Il est la somme de deux vecteurs :

Cas particulier du mouvement circulaire uniforme
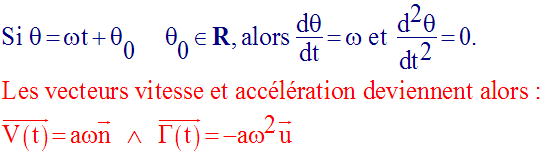
Le vecteur-accélération devient tel que sa direction est normale à la trajectoire.
Par ailleurs, on a :
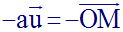
Donc,
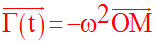
Applications
1-
Un point mobile M se
déplace sur un axe orienté (x’x) tel que son abscisse, à tout instant t
est égale à :
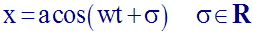
Détermine son vecteur-vitesse et son vecteur accélération à tout instant t.
2-
On te donne un point mobile M se déplaçant dans le plan muni d’un repère orthonormal.
Ses coordonnées à tout instant t sont données par le système :
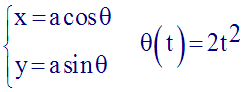
Sans faire des calculs, démontre que son mouvement circulaire n’est pas uniforme.
Détermine ses vecteurs vitesse et accélération.
Je te laisse faire ces deux applications.