
1- Nombres premiers
Un entier naturel est dit premier si et seulement si ses seuls diviseurs sont 1 et lui-même.
Exemples :
Les seuls diviseurs de 7 sont 1 et 7; donc 7 est un nombre premier.
Les seuls diviseurs de 2 sont 1 et 2; donc 2 est un nombre premier.
Les seuls diviseurs de 19 sont 1 et 19; donc 19 est un nombre premier.
Les diviseurs de 4 sont 1 et 2 et 4; donc 4 admet au moins un
diviseur, 2,
différent de 1 et de 4. Donc 4 n'est pas un nombre premier.

2- Notion de pgdc de nombres entiers naturels
2-1- Définition
Etant donné deux entiers naturels a, b avec b non nul.
Il existe au moins un entier naturel q, appelé quotient, tel que :
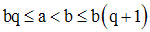
Il existe un couple et un seul, (q , r), élément de N2 tel que :
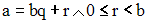
Soient deux entiers naturels quelconques p, q.
L’ensemble des diviseurs de p est noté Dp et celui des diviseurs de q, Dq .
L’ensemble des diviseurs communs à p, q est donc :
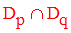
Le plus grand des éléments de cette intersection est
appelé plus grand diviseur commun à p et q
et sera noté pgdc
(p , q).
Exemple :
On donne 144 et 36.
Définis par extension D144 et D36
Définis par extension :

Solution
On écrit d’abord les nombres sous la forme d’un produit de puissances de facteurs premiers.
La division de 144 par 2 donne
72 ; la division de 72 par 2 donne 36 ; la
division de 36 par 2 donne 18 ;
la division de 18
par 2 donne 9 ; la division de 9 par
3 donne 3 et la division de 3 par
3 donne 1.
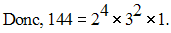
La division de 36 par 2 donne
18 ; la division de 18 par 2 donne 9 ; la
division de 9 par 3 donne 3 et
la division de 3
par 3 donne 1.
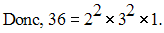
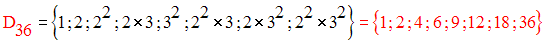

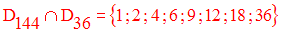
pgdc(144 , 36)
= 36
2-2- Propriété
Soient a et b deux entiers naturels non nuls.
Soit D = pgdc (a , b).
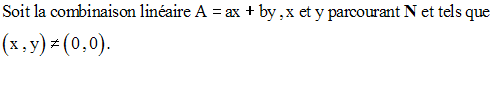
Lorsque x et y varient, A varie et, pour certaines valeurs xp et yp , A admet une valeur minimum que l’on note m.
On a donc :
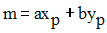
On suppose que m ne divise pas a.
La division euclidienne de a par m donne :
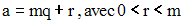
En tirant r de cette égalité, on obtient :
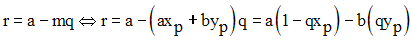
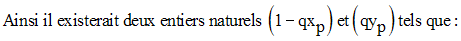
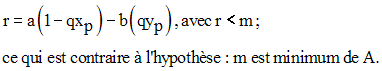
Conclusion : m divise a.
On procède par la même démonstration par l’absurde, pour démontrer que m divise également b.
Par ailleurs, D étant le pgdc de a et b, il existe au moins
deux entiers naturels non nuls, A et B,
tels que : a = A . D et b = B . D
On exprime m en fonction de A, B et D :

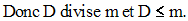
Ainsi, D et m sont diviseurs communs de a et b.
Or, D est le plus petit ; donc m ne peut lui être inférieur.
Par conséquent m = D.
Conclusion :

2-3- Conséquence
Soit D = pgdc (a , b).
Soit d un diviseur commun quelconque de a et b.
Montre que :
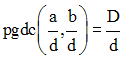
En déduis que :
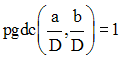
Solution
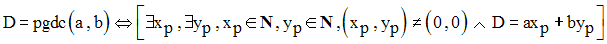
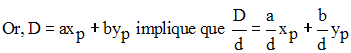
On peut donc écrire :
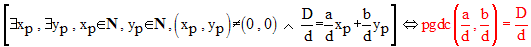
Par ailleurs, on a :
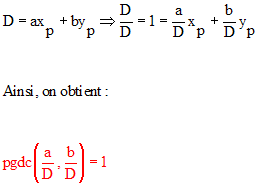
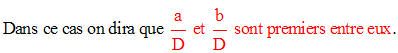
C'est le théorème de Bizout.
D’où la définition :
Deux nombres entiers naturels sont dits premiers entre eux si et seulement si leur pgdc est égal à 1.
On dira également que plusieurs entiers naturels
sont premiers entre eux dans leur ensemble
si et seulement si leur pgdc est égal à 1.
2-4- Algorithme d'Euclide
Soient deux nombres entiers naturels non nuls quelconques tels que A soit strictement supérieur à B.
Soit G le pgdc de A et B ; on écrit :
G = pgdc (a , b)
La division euclidienne donne :
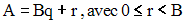
1er cas : r = 0
Dans ce cas B divise A, et comme B est strictement inférieur à A, G est égal B.
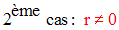
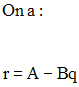
Soit g un diviseur commun quelconque à A et B.
g divisant A et B, divisera A, Bq et leur somme A – Bq = r.
Ainsi, tout diviseur commun à A et B, divise r.
On cherche tous les diviseurs communs à B et r.
On a les divisions successives suivantes :
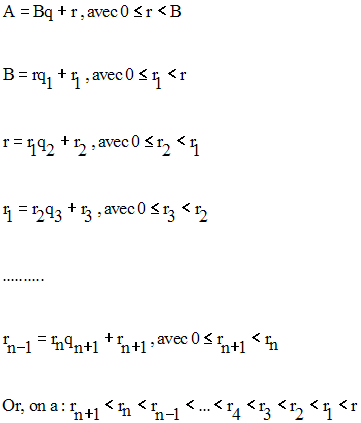
Cette suie de nombres entiers naturels est décroissante. Elle admet donc un terme minimum.
Deux cas sont donc possibles :
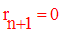
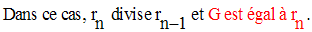
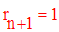

Donc G = 1 et A, B sont premiers entre eux.
Exemples d'application de l'algorithme d'Euclide
Si on applique l’algorithme à notre exemple précédent, on écrit :
144 = 36 . 4 + 0
On est dans le 1er cas où r = 0.
Donc G = 36
Trouvons le pgdc de 1248 et 144.
On a successivement :
1248 = 144 . 8 + 96
144 = 96 . 1 + 48
96 = 48 . 2 + 0
Donc G = 48.
2-5- Théorème de Gauss
Montre que si un entier naturel
divise le produit de deux entiers naturels et est premier avec l’un
des
facteurs
du produit, alors il divise l’autre facteur.
C’est le théorème de Gauss.
Démonstration
Par hypothèse , on a m et n deux entiers naturels non nuls ; p
un entier naturel non nul divisant
m . n et premier avec m.
On démontre que p divise n.
p étant premier avec m, on peut appliquer le théorème de Bezout :
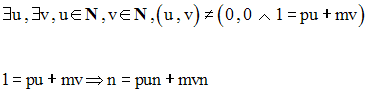
p divisant p et mn, divisera pun et mnv et leur somme n.
3- Notion de ppmc de nombres entiers naturels
3-1- Définition
Soient deux entiers naturels quelconques p, q.
L’ensemble des multiples de p est noté Mp et celui des multiples de q, Mq .
L’ensemble des multiples communs à p et q est donc :
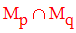
Le plus petit des éléments non
nuls de cette intersection est
appelé plus petit multiple commun à p et q
et est noté ppmc
(p, q).
Exemple :
Calcule ppmc (26,39)
Solution

3-2- Relation liant les pgdc et ppmc de deux entiers naturels
Soient a, b deux entiers naturels quelconques.
Posons m et n respectivement leurs pgdc et ppmc.
Montre que :
ab = mn
Démonstration
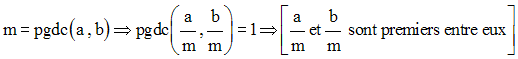
Par ailleurs, on peut écrire :
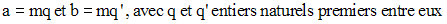
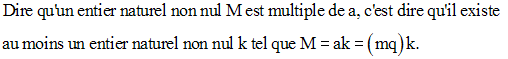
Dire que M est également multiple de b, c’est dire que b divise
(mq)k ou que mq’ divise mqk
ou encore q’ divise qk.
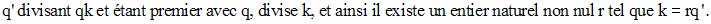
On écrit donc la forme générale des multiples communs de a et b :

4- Généralisation
Les notions de pgdc et ppmc s’appliquent à plusieurs nombres entiers naturels.
Exemples :
pgdc (4, 6, 12, 36, 144) ; ppmc (4, 18, 156)
5- Le système binaire
5-1
On te donne 13 articles.
On te demande de regrouper ces articles par paquets de deux
puis ensuite de constituer avec
ces paquets des
cartons contenant chacun deux paquets.
Ces cartons sont à leur tour regroupés par deux dans des colis.
Combien de colis, de cartons et de paquets a-t-on pu ainsi former ?
Solution
Je divise 13 par 2 ; j’obtiens 6 paquets et il me reste 1 article.
Je divise 6 par 2 ; j’obtiens 3 cartons et il me reste 0 paquet.
Je divise 3 par 2 ; j’obtiens 1 colis et il me reste 1 carton.
Ainsi, j’ai constitué 1 colis, 1 carton et il me reste 1 article.
De ce petit exercice découle le langage commun à tous les ordinateurs : le système binaire.
5-2
Ecris dans le système binaire les entiers naturels suivants :
5, 13, 17 et 19.
Solution
Je divise 5 par 2 ; j’obtiens 2 et il me reste 1.
Je divise 2 par 2 ; j’obtiens 1 et il me reste 0.
Ainsi, 5, écris dans le système décimal
sera égal à 101 dans le système binaire
(parfois on dit aussi « base 2 »).
Je divise 13 par 2 ; j’obtiens 6 et il me reste 1.
Je divise 6 par 2 ; j’obtiens 3 et il me reste 0.
Je divise 3 par 2 ; j’obtiens 1 et il me reste 1.
Ainsi, 13, écris dans le système décimal sera égal à 1101 dans le système binaire.
Je divise 17 par 2 ; j’obtiens 8 et il me reste 1.
Je divise 8 par 2 ; j’obtiens 4 et il me reste 0.
Je divise 4 par 2 ; j’obtiens 2 et il me reste 0.
Je divise 2 par 2 ; j’obtiens 1 et il me reste 0.
Ainsi, 17, écris dans le système décimal sera égal à 10001 dans le système binaire.
Je divise 19 par 2 ; j’obtiens 9 et il me reste 1.
Je divise 9 par 2 ; j’obtiens 4 et il me reste 1.
Je divise 4 par 2 ; j’obtiens 2 et il me reste 0.
Je divise 2 par 2 ; j’obtiens 1 et il me reste 0.
Ainsi, 19, écris dans le système décimal sera égal à 10011 dans le système binaire.
5-3
Effectue les opérations suivantes dans le système binaire :
1101 + 1001 ; 1111 + 11011 ; 111 × 11.
Solution
Je pose mes opérations comme dans le système décimal ; puis je
les effectue en prenant le soin
de convertir les résultats dans le système
binaire.
Ainsi, pour effectuer 1101 + 1001, je dis :
1 et 1 font 2 et dans le système binaire, 2 vaut 10. Donc, je pose 0 et je retiens 1.
1 + 0 + 0 = 1.
1 + 0 = 1.
1 et 1 font 2 et dans le système binaire, 2 vaut 10. Donc, je pose 10.
Finalement, 1101 + 1001 = 10110.
Même méthode pour effectuer 1111 + 11011 et je trouve :
1111 + 11011 = 101010
Pour effectuer 111 × 11, j’effectue d’abord ma multiplication
comme si je travaillais dans le
système décimal ; puis, j’effectue mes additions
partielles en prenant le soin de convertir, s’il y lieu,
dans le système
binaire.
1 1 1
1 1
____
1 1 1
1 1 1
____
1 0 1 1 1
Finalement, 111 × 11 = 10111.
5-4
Convertis dans le système décimal les nombres suivants écrits dans le système binaire :
11, 101, 100, 1101.
Solution
11 (base 2) = 1 ´ 20 + 1 ´ 21 (base 10) = 1 + 2 (base 10) = 3 (base 10)
101 (base 2) = 1 ´ 20 + 0 ´ 21 + 1 ´ 22 (base 10) = 1 + 0 + 4 (base 10) =
5 (base 10)
100 (base 2) = 0 ´ 20 + 0 ´ 21 + 1 ´ 22 (base 10) = 0 + 0 + 4 (base 10) =
4 (base 10)
1101 (base 2) = 1 ´ 20 + 0 ´ 21 + 1 ´ 22 + 1 ´ 23 (base 10) =
1 + 0 + 4 + 8 (base 10) = 13 (base 10)
6- Un système intéressant
6-1
On te donne 1260 articles.
On te demande de regrouper ces articles par paquets de
douze puis ensuite de constituer avec ces paquets
des cartons contenant chacun douze paquets.
Combien de cartons et de paquets a-t-on pu ainsi former ?
De ce petit exercice découle le système do décimal.
Dans ce système tout entier naturel est écrit avec les chiffres 0, 1, 2, 3, … , 10, 11.
Pour lever toute ambiguïté dans les écriture on posera :
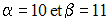
6-2
Convertis dans le système do décimal les nombres suivants écrits dans le système décimal :
12, 15, 177, 5040.
6-3
Convertis dans le système décimal les nombres suivants écrits dans le système do décimal :
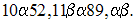
6-4
Effectue l'opération suivante dans le système do décimal :

6-5
Convertis dans le système binaire le nombre suivant écrit dans le système do décimal :

Solution
6-1
Je divise 1260 par 12 ; j’obtiens 105 paquets et il me reste 0 article.
Je divise 105 par 12 ; j’obtiens 8 cartons et il me reste 9 paquets.
Ainsi, j’ai constitué 8 cartons et 9 paquets.
6-2
12 (base 10) = 10 (base 12)
15 (base 10) = 13 (base 12)
177 (base 10) = 129 (base 12)
5040 (base 10) = 2b00 (base 12)
6-3
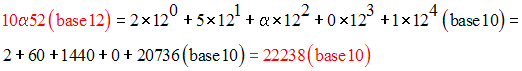
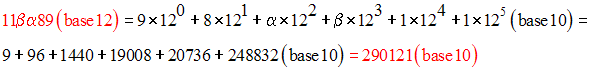
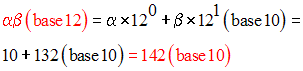
6-4
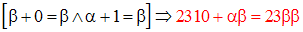
6-5

7- Progressions
7-1 Progressions arithmétiques

La constante r est appelée raison de la progression.
Exemple :
La suite définie par :
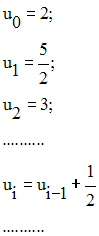
est une progression arithmétique de raison r = 0,5 et de premier terme u0 .
Propriétés
Soit une progression arithmétique de premier terme u0 et de raison r.
1-
On a donc :
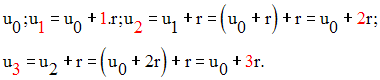
Supposons que cette propriété est vraie pour n – 1 et montrons qu’elle l’est pour n.
On a donc :
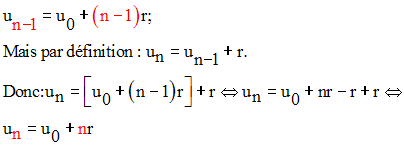
2-

Supposons que cette seconde propriété est vraie pour l’indice p, p entier naturel tel que 2 < p < n :
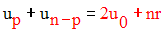
Montrons qu’elle l’est pour l’indice p + 1.
On a :
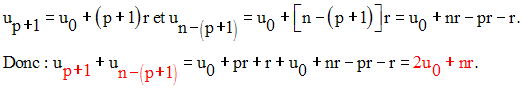
On dira que dans une progression arithmétique, la
somme des termes équidistants est
constante et est égal 2u0 + nr.
3-
Cette propriété permet de calculer la somme des termes d’une progression arithmétique.
En effet, on a :
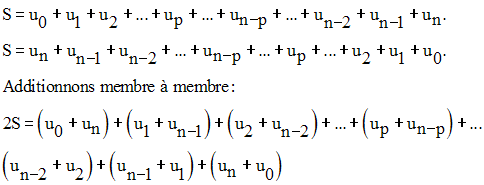
Mais aussi :
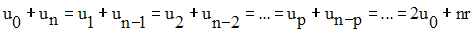
Donc finalement on obtient :
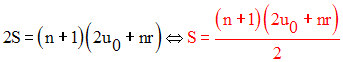
C’est la somme des (n + 1)
premiers termes d’une progression arithmétique de premier terme
u0
et de raison r.
On aurait pu également écrire :
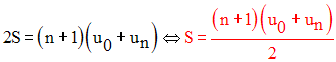
Exercices
1)
Calcule la somme des 100 premiers entiers naturels 0, 1, …, 99.
Solution
La raison de cette progression arithmétique est 1.
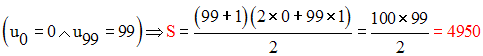
2)
Calcule la somme des 100 premiers entiers naturels impairs et celle des 100 premiers entiers naturels pairs.
3)
Une progression arithmétique de n termes a pour somme S et
pour dernier terme m.
Calcule son premier terme a et sa raison.
Application : n = 5, S = 65 et m = 29.
Solution
Soit u0 le premier terme et r la raison.
u0 étant le premier terme et comme il y a n termes, le nième terme est un – 1.
Donc, on a :
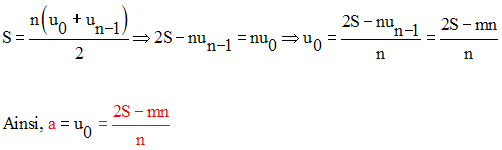
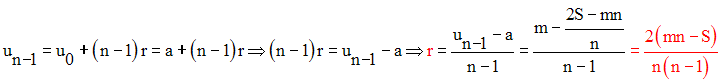
Application numérique :
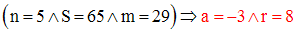
4)
Une progression arithmétique a pour raison 3, pour dernier
terme 12 et pour somme 30.
Calcule le premier terme a et le nombre de termes n.
Solution
On a : r = 3, b = 12 et S = 30.

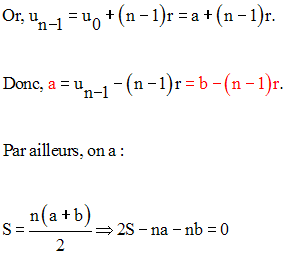
Dans cette dernière équation, on remplace a par son égale b – (n – 1)r.
On obtient :
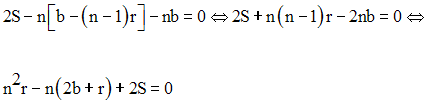
On a donc une équation du second degré dont l’inconnue est n.
Dans cette équation, en remplaçant r, b et S par leurs valeurs respectives, on obtient :
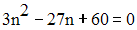
Le discriminant D de cette équation est égale à :
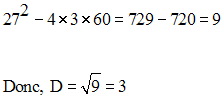
Les racines sont :
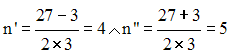
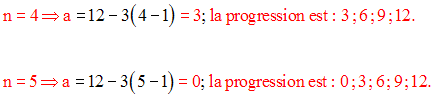
5)
Trouve cinq nombres en progression arithmétique connaissant leur somme 15 et la somme de leurs carrés 65.
Solution
Conseil : chaque fois qu’un énoncé fait intervenir la somme des
termes d’une progression arithmétique,
il est judicieux d’écrire la progression
sous sa forme symétrique :
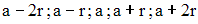
D’après les hypothèses de l’énoncé, on obtient :

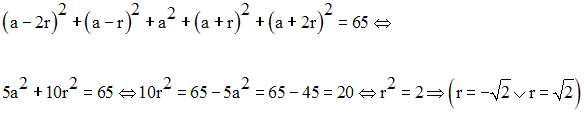
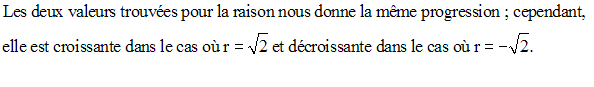
Ainsi, les nombres sont :
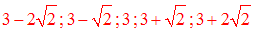
6)
a- Dans un triangle (ABC) les côtés a, b, c sont en
progression arithmétique de raison k.
Montre que si Ra , Rb , Rc
sont les rayons des cercles exinscrits respectivement dans les angles
A, B et C, alors :
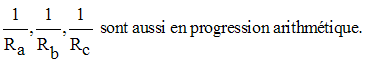
b- Connaissant b et k, calcule Ra , Rb , Rc . Discussion.
c- Connaissant Ra et Rc , calcule a, b et c. Discussion.
7)
Dans une progression arithmétique de n termes, de premier terme a, de dernier terme l et de raison r, on pose :
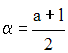
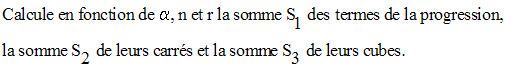
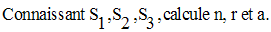
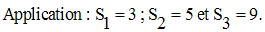
7-2 Progressions géométriques

La constante q est appelée raison de la progression.
Exemple :
La suite numérique définie par :
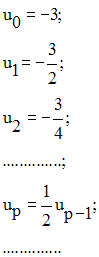
est une progression géométrique de premier terme -3 et de raison 0,5.
Propriétés
Soit une progression géométrique de premier terme u0 et de raison q réel non nul.
1-
On a :
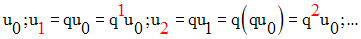
Supposons cette propriété vraie pour l’indice i; donc :
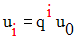
Montrons qu’elle l’est pour l’indice i + 1 :
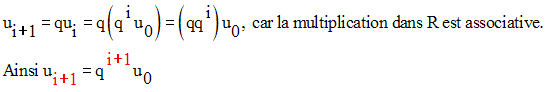
2-
Supposons, pour la suite, que cette progression a n termes u0 , u1 , u2 , u3 , …, un-1
Posons P le produit de ces n termes.
On a :
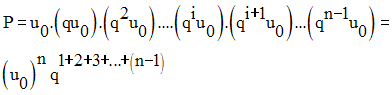
On sait que :
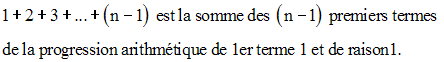
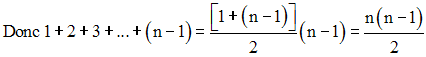
Ainsi,
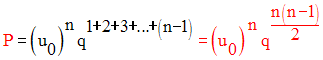
Posons S la somme des termes de la progression géométrique.
On a :
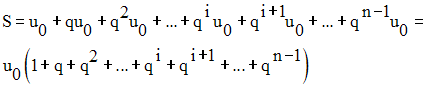

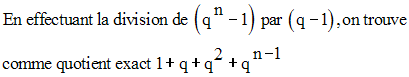

Finalement on obtient :
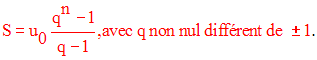
Exercices
1)
Une progression géométrique de raison 2 se compose de six
termes et sa somme est 189.
Calcule le premier et le dernier terme.
Solution
Si u0 est le premier terme, alors le sixième sera u5 et on a :

Par ailleurs, on a :
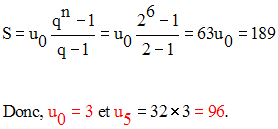
2)
Trouve trois nombres en progression géométrique connaissant leur somme 36,75 et leur produit 343.
Solution
Conseil : chaque fois qu’un énoncé fait intervenir la somme des
termes d’une progression géométrique,
il est judicieux d’écrire la progression
sous sa forme symétrique :
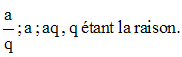
D’après les hypothèses de l’énoncé, on a :
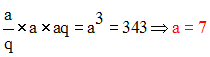
Par ailleurs, on a :
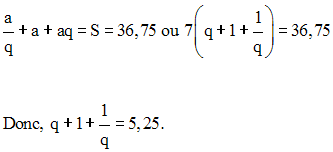
q étant non nulle, cette dernière équation en q peut s’écrire :
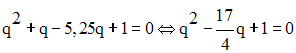
La résolution de cette équation en q donne :
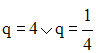
Les deux valeurs de q donnent les mêmes nombres écrits dans un ordre ou dans l’autre.

3)
Trouve trois nombres en progression géométrique connaissant leur somme et celle de leurs carrés :
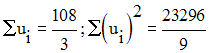
4)
Les trois côtés d’un triangle sont en progression géométrique. Entre quelles limites est comprise sa raison ?
Un tel triangle peut-il être rectangle ?